探索迷人的密码世界

在数字领域，加密技术作为强大的屏障，以精密的方式保护我们的秘密。植根于数学和逻辑，它代表了人类智慧的顶峰。除了简单的代码和算法之外，加密是一门严格的科学，能够以无与伦比的精度将明文转换为密文......

历史中的精彩时刻

了解 SHA-256：一种安全哈希算法

SHA-256，属于SHA-2（安全哈希算法 2）家族，是一种由国家安全局（NSA）设计并由国家标准与技术研究院（NIST）发布的加密哈希函数。旨在替代较旧的 SHA-1，SHA-256 提供了增强的安全性，并在包括 TLS/SSL、PGP、SSH、IPsec 以及比特币等区块链技术中发挥着关键作用。

作为最安全的哈希算法之一，SHA-256在数字安全和完整性检查中扮演着关键角色。尽管理论上存在碰撞的可能性，但实际上找到两个不同的输入产生相同输出哈希几乎是不可能的，这使得 SHA-256 成为抵御攻击的强大工具。

随着技术的发展，持续评估 SHA-256 的安全性至关重要。我们的指南深入浅出地探讨了 SHA-256 的复杂细节，尽可能确保读者理解这一算法在维护数字安全中的重要性。当然，您也可以使用下面的网页测试您的哈希知识。

哈希值测试的主要优势和应用

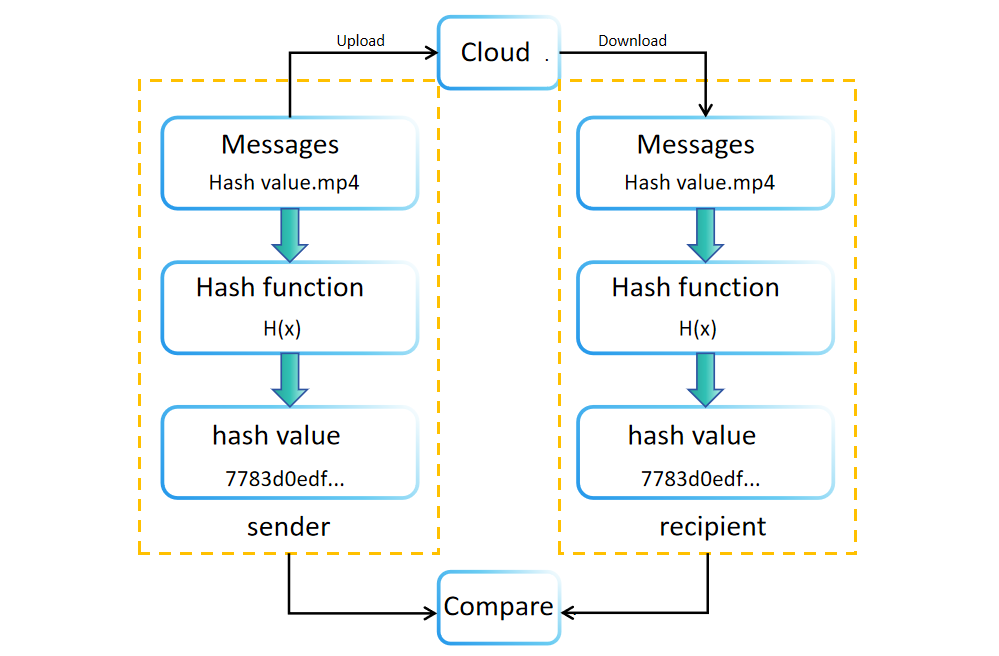
比较哈希值的过程
比较哈希值的过程

摩尔斯电码：19世纪先驱通信系统

摩尔斯电码，由美国艺术家兼发明家萨缪尔·摩尔斯在1830年代开发，通过引入使用点（短信号）和划（长信号）来编码字母、数字和标点符号的编码系统，彻底革新了电信领域。这一创新促进了通过电报线路的传输，成为19世纪及20世纪初海上通信中的基石。

想要全面探索摩尔斯电码，请访问摩尔斯电码编译器页面。

解码摩尔斯电码信号

摩尔斯电码中字符的独特表示方法，通过短信号和长信号以及特定的间隔，允许在不同平台上进行清晰的通信：

摩尔斯电码的持久影响

尽管出现了更先进的通信技术，摩尔斯电码仍然是通信历史上的一个标志性人物，影响着许多后续技术，并在无线电爱好者和特定领域的专业人士中保留着特殊的地位。

其简单性和高效性使摩尔斯电码在现代通信基础设施不可用的情况下成为可靠的替代方案，为历史学家和技术爱好者搭建了沟通历史创新与当前实践的桥梁。

探索摩尔斯电码

本页面提供了关于以下内容的见解：

了解恺撒密码：加密、解密及破解

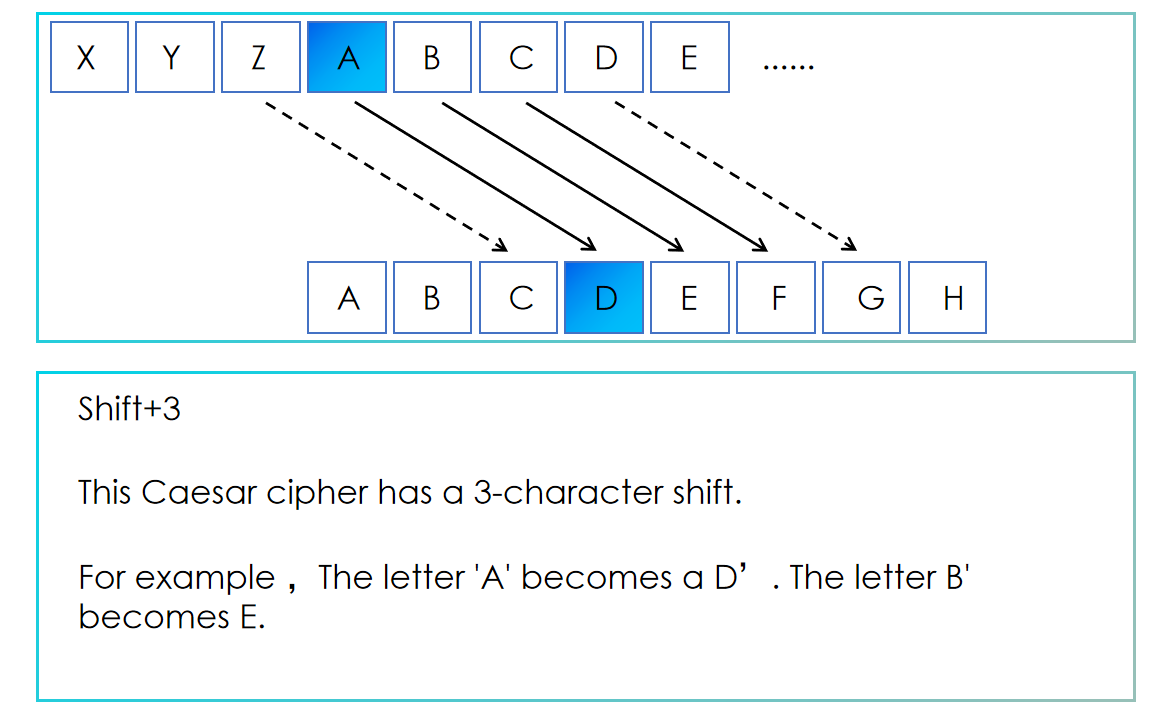
恺撒密码， 因尤利乌斯·恺撒在保障军事通信的安全中使用而得名，代表了一种基本的替代密码技术。 在这种方法中，明文中的字母被替换为字母表中固定位置上或下的另一个字母。 尽管其简单性，但在特定的历史条件下和基本密码分析技术盛行的时代，恺撒密码还是非常有效的。

如今，尽管容易被破解，恺撒密码仍然是密码学中的一个重要教学工具，展示了基本的加密技巧，如字母移位。 它是理解更复杂的密码系统的基础，因其历史意义和简单性仍然是研究的一个焦点。

本页面将探讨：

恺撒密码示意图
恺撒密码示意图

理解普莱菲尔密码：19世纪的加密奇迹

普莱菲尔密码，一个由查尔斯·惠斯通于1854年创造的开创性手动对称的加密方法，因为是首个使用双字母替换密码的系统而脱颖而出，增强了电报通信的安全性。尽管惠斯通是发明者，但它自豪地承载了普莱菲尔勋爵的名字，他在推广该密码中发挥了重要作用。

全球采用及其在军事战略中的重要性

最初被英国外交部认为过于复杂，普莱菲尔密码在第二次布尔战争和第一次世界大战等关键时刻在英国军队中获得了广泛的接受。到了20世纪40年代，它已被澳大利亚、德国和新西兰等国家使用，证明了在第二次世界大战中的重要性。

现代用途：教育和娱乐目的

现代计算机的出现降低了普莱菲尔密码的安全性及有效性。如今，它主要作为教育目的和娱乐密码学的工具，提供了一个通往密码技术迷人世界的入口。在这个过程中，您将：

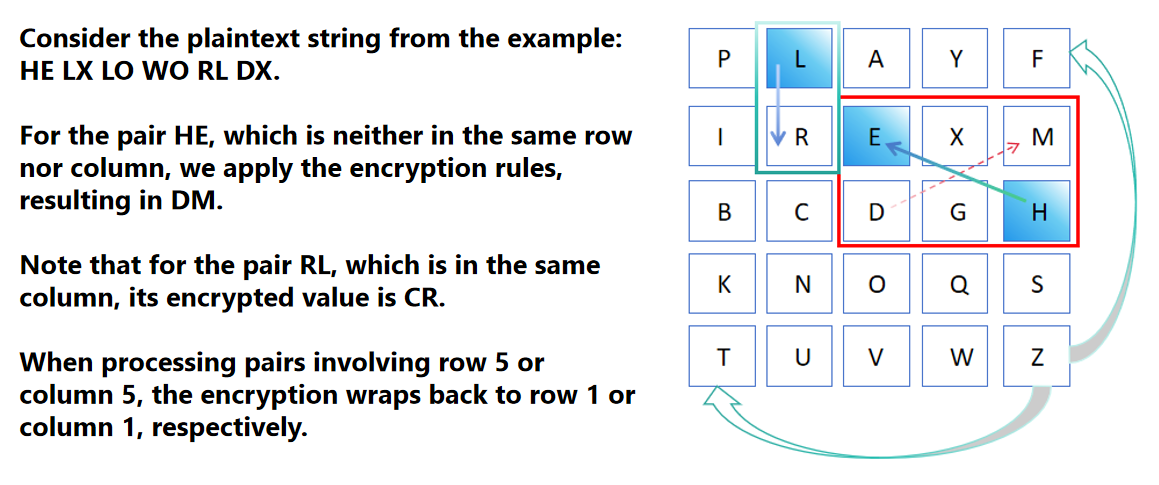
普莱菲尔密码密钥矩阵的详细视图
普莱菲尔密码密钥矩阵的详细视图

理解希尔密码：一个全面的指南

希尔密码，由莱斯特·S·希尔在1929年设计的关键加密技术，在经典密码学领域因其独特应用线性代数和矩阵理论而与众不同。与其前身不同，希尔密码采用矩阵乘法进行加密，要求密钥：一个矩阵，对算法有效运行必须是可逆的。

这种高级密码技术将字母块作为单个单元加密，提高了其复杂性，并使其从传统的替代密码中显著脱颖而出。下面，我们将深入探讨希尔密码的数学基础和操作机制：

  • 字符的矩阵表示：为字母分配数值（例如，A=0, B=1, ..., Z=25）并将信息分成块，表示为n维向量。
  • 密钥矩阵：一个必须在模26下可逆的n x n矩阵，以确保可解密性。
  • 加密过程：涉及将密钥矩阵与明文块向量相乘，模26。
  • 解密过程：通过乘以密钥矩阵的逆矩阵与加密向量相乘，模26来实现。

希尔密码的安全性主要依赖于执行模26的矩阵逆转的复杂性。然而，它仍然容易受到已知明文攻击，并且需要调整明文长度以匹配矩阵大小，通常需要额外的填充。

尽管存在这些漏洞，希尔密码仍因其在传播密码学基础知识方面的教育价值而受到赞扬。虽然它在现代应用中的实际用途可能有限，但它在密码学教育和研究中是依旧是一个关键的垫脚石。

学习成果：

  • 掌握希尔密码的工作原理及其加密步骤。
  • 学习希尔密码在加密和解密消息中的应用。
  • 理解线性代数和矩阵理论在希尔密码中的核心作用。
  • 明白希尔密码和普莱菲尔密码之间的区别。

了解四方密码：密码学历史的关键

密码的定义

Félix Delastelle 在他的书 Traité Élémentaire de Cryptographie 中提供了以下定义：

On appelle cryptographie la science qui a pour objet l'étude des moyens susceptibles d'assurer le secret des correspondances ou écrits qu'on a intérêt à soustraire à la curiosité des tiers ou à l'indiscrétion des intermédiaires. En d'autres termes, la cryptographie enseigne à transformer un langage clair en langage secret.

Delastelle 强调，密码学是一门科学而非艺术。他认为，加密在给定特定方法和密钥时，会生成一个独特的明文版本，类似于算术运算。这突显了密码过程的结构化和科学性，与解密的解释性和可变性形成对比。

四方密码的工作原理

四方密码使用四个5x5矩阵来加密二联字。以下是密码工作原理的详细分解：

准备： 创建四个5x5的方格（网格）。左上角和右下角的方格包含标准字母表（去掉'J'以适应25个字母）。右上角和左下角的方格用混合或基于关键字的字母表填充。这些混合字母对于密码的安全性至关重要。

加密二联字：

步骤1： 将明文消息分成二联字（字母对）。如果字母数量是奇数，则添加一个额外的字母，如'X'，以完成最后一对。

步骤2： 对于每个二联字，在左上方格中找到第一个字母，在右下方格中找到第二个字母。

步骤3： 确定这些字母在各自方格中的坐标（行和列）。

步骤4： 使用这些坐标在右上方格和左下方格中找到对应的字母。在右上方格中，与第一个明文字母在同一行但在第二个明文字母的列中的字母成为密文二联字的第一个字母。同样，在左下方格中，与第二个明文字母在同一行但在第一个明文字母的列中的字母成为密文二联字的第二个字母。

示例： 加密二联字"HI"。

步骤1： 在左上方格中找到'H'，在右下方格中找到'I'。假设'H'位于左上方格的第2行第3列，'I'位于右下方格的第3行第4列。

步骤2： 在混合字母表中找到这些坐标上的字母。在右上方格中，找到第2行第4列的字母。在左下方格中，找到第3行第3列的字母。

步骤3： 将这些字母组合形成密文二联字。

解密： 解密过程涉及反向这些步骤。接收者必须知道方格的排列和使用的混合字母。通过在右上方格和左下方格中找到密文字母并将其映射回左上方格和右下方格中的对应明文字母，可以重建原始消息。

四方密码加密示意图
四方密码加密示意图

通过浏览页面，您将学习到：

此外，通过阅读 Traité Élémentaire de Cryptographie，您将对密码学有更深入的了解。通过互动教程和示例，您将深入探讨这种经典加密方法的复杂性和魅力。

加密技术的真正魅力在于它体现了人类对自由和隐私不懈追求的象征。在这个建立在数据之上的世界里， 它提醒我们，尽管面临着无数挑战，只要我们拥有智慧和勇气，就能在数字时代保护我们最珍贵的宝藏。