播放/暫停
在數字領域,加密技術作為強大的屏障,以精密的方式保護我們的秘密。植根於數學和邏輯,它代表了人類智慧的頂峰。除了簡單的代碼和算法之外,加密是一門嚴格的科學,能夠以無與倫比的精度將明文轉換為密文......
歷史中的精彩時刻
凱撒密碼的使用(古代)
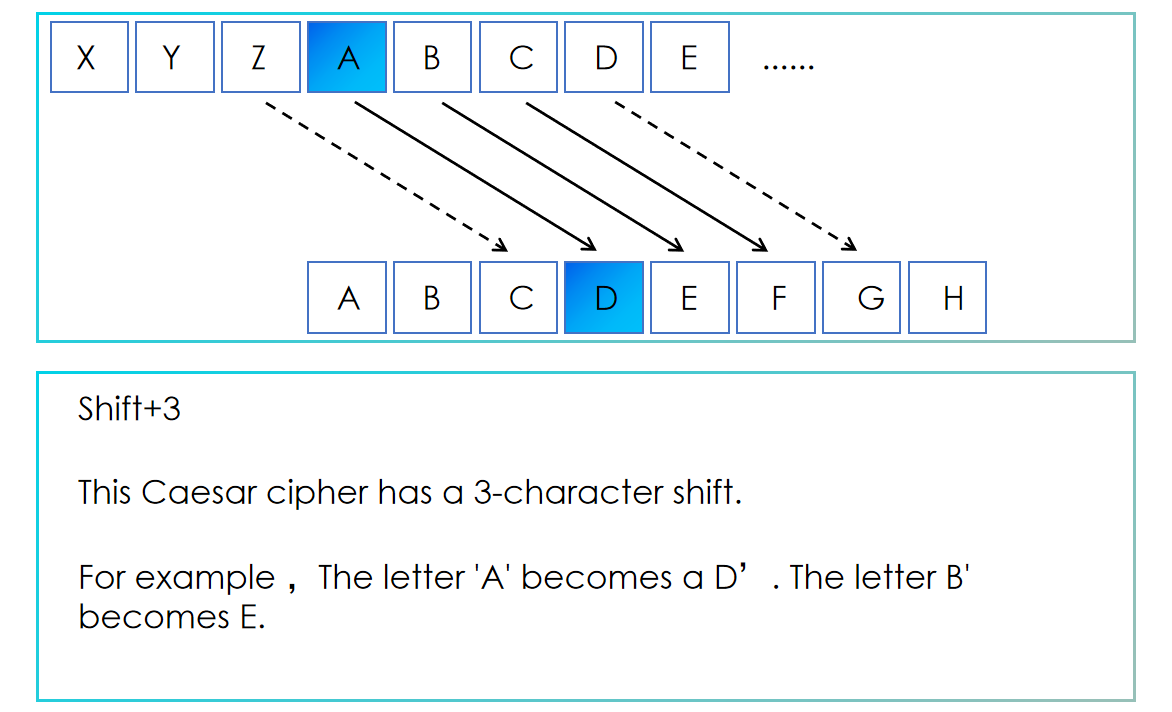
凱撒密碼 ,由羅馬將軍凱撒發明,是一種簡單的替換密碼,通過將字母表中的每個字母替換為後面固定位置的字母來加密。
維吉尼亞密碼的發明(1467年)
維吉尼亞密碼 ,一種多表替換密碼,由意大利密碼學家喬瓦尼·巴蒂斯塔·貝拉索 發明。它使用多個替換字母表來加密信息。
吉爾伯特·維爾南發明一次性密碼本(1917年)
吉爾伯特·維爾南 發明了一次性密碼本,這是一種理論上無法破解的加密方法,通過使用與明文長度相同的隨機密鑰進行加密。
柯爾莫哥洛夫複雜性理論的提出(1943年)
安德烈·柯爾莫哥洛夫提出了複雜性理論,為現代密碼學奠定了理論基礎。
迪菲-赫爾曼密鑰交換協議的提出(1976年)
惠特菲爾德·迪菲和馬丁·赫爾曼提出了迪菲-赫爾曼密鑰交換協議,使公鑰密碼學成為可能。
RSA算法的發明(1977年)
羅納德·李維斯特、阿迪·薩米爾和倫納德·阿德爾曼發明了RSA算法 ,這是一種基於大數分解難度的公鑰加密算法。
橢圓曲線密碼學的提出(1985年)
尼爾·科布利茲和維克托·米勒分別提出了橢圓曲線密碼學(ECC),這是一種基於橢圓曲線數學結構的公鑰加密技術。
PGP(相當好的隱私)發布(1991年)
菲爾·齊默爾曼發布了PGP,這是一種廣泛用於保護電子郵件和文件的加密軟件。
AES(高級加密標準)競賽的啟動(1997年)
國家標準與技術研究院(NIST)啟動了AES競賽,以尋找取代DES的對稱加密標準。2000年,Rijndael算法被選為AES(高級加密標準),成為新的對稱加密標準。
SHA-2雜湊算法的發布(2004年)
國家安全局(NSA)發布了SHA-2 系列雜湊算法,用於數據完整性驗證和數字簽名。
量子密碼學的突破(2010年)
量子密碼學在量子密鑰分發(QKD)方面取得了重大突破,為未來的信息安全提供了新的方向。
TLS 1.3協議的開發(2015年)
TLS 1.3協議的開發開始,旨在提高互聯網通信的安全性和效率,並於2018年正式發布。
了解 SHA-256:一種安全哈希算法
SHA-256 ,屬於SHA-2(安全哈希算法 2)家族 ,是一種由國家安全局(NSA)設計並由國家標準與技術研究院(NIST)發布的加密哈希函數。旨在替代較舊的 SHA-1,SHA-256 提供了增強的安全性,並在包括 TLS/SSL、PGP、SSH、IPsec 以及比特幣等區塊鏈技術中發揮著關鍵作用。
作為最安全的哈希算法之一,SHA-256 在數字安全和完整性檢查中扮演著關鍵角色。儘管理論上存在碰撞的可能性,但實際上找到兩個不同的輸入產生相同輸出哈希幾乎是不可能的,這使得 SHA-256 成為抵禦攻擊的強大工具。
隨著技術的發展,持續評估 SHA-256 的安全性至關重要。我們的指南深入淺出地探討了 SHA-256 的複雜細節,盡可能確保讀者理解這一算法在維護數字安全中的重要性。當然,您也可以使用下面的網頁測試您的哈希知識 。
哈希值測試的主要優勢和應用
理解哈希函數的特性和應用領域。
深入了解廣泛使用的哈希函數及其運作原理。
實用指南,用於使用 SHA-256 驗證數字文件的完整性和真實性。
探索其他主流哈希函數及其機制。
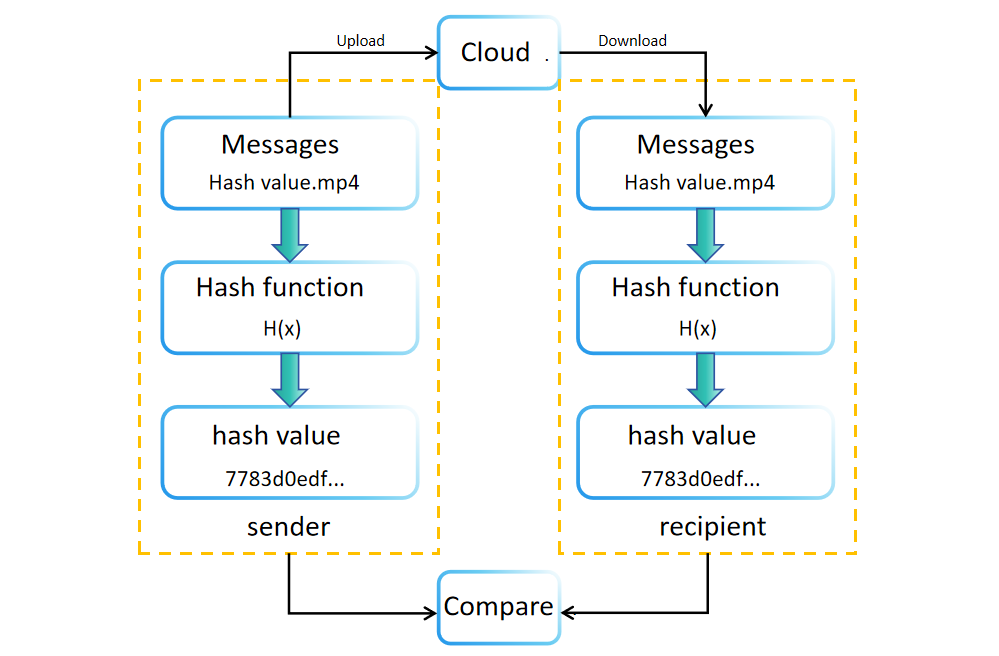
比較哈希值的過程
摩爾斯電碼:19世紀先驅通信系統
摩爾斯電碼 ,由美國藝術家兼發明家薩繆爾·摩爾斯在1830年代開發,通過引入使用點(短信號)和劃(長信號)來編碼字母、數字和標點符號的編碼系統,徹底革新了電信領域。這一創新促進了通過電報線路的傳輸,成為19世紀及20世紀初海上通信中的基石。
想要全面探索摩爾斯電碼,請訪問摩爾斯電碼編譯器 頁面。
解碼摩爾斯電碼信號
摩爾斯電碼中字符的獨特表示方法,通過短信號和長信號以及特定的間隔,允許在不同平台上進行清晰的通信:
點(".") :代表短信號。劃("-") :代表長信號。字符內暫停 :用於區分字符內的點和劃。字母間暫停 :用於分隔字母,以便閱讀。詞間分隔暫停 :在通信中用於區分單詞。
摩爾斯電碼的持久影響
儘管出現了更先進的通信技術,摩爾斯電碼仍然是通信歷史上的一個標誌性人物,影響著許多後續技術,並在無線電愛好者和特定領域的專業人士中保留著特殊的地位。
其簡單性和高效性使摩爾斯電碼在現代通信基礎設施不可用的情況下成為可靠的替代方案,為歷史學家和技術愛好者搭建了溝通歷史創新與當前實踐的橋樑。
探索摩爾斯電碼
本頁面提供了關於以下內容的見解:
摩爾斯電碼的歷史演變和重要性。
理解摩爾斯電碼的操作動態。
摩爾斯電碼的技術層面和應用,包括其字母表。
了解凱撒密碼:加密、解密及破解
凱撒密碼 ,
因尤利烏斯·凱撒在保障軍事通信的安全中使用而得名,代表了一種基本的替代密碼技術。
在這種方法中,明文中的字母被替換為字母表中固定位置上或下的另一個字母。
儘管其簡單性,但在特定的歷史條件下和基本密碼分析技術盛行的時代,凱撒密碼還是非常有效的。
如今,儘管容易被破解,凱撒密碼仍然是密碼學中的一個重要教學工具,展示了基本的加密技巧,如字母移位。
它是理解更複雜的密碼系統的基礎,因其歷史意義和簡單性仍然是研究的一個焦點。
本頁面將探討:
凱撒密碼加密和解密的原理。
如何使用在線工具進行文本的加密或解密。
使用Python破解凱撒密碼的技巧。
凱撒密碼示意圖
理解普萊菲爾密碼:19世紀的加密奇蹟
普萊菲爾密碼 ,一個由查爾斯·惠斯通 於1854年創造的開創性手動對稱的加密方法 ,因為是首個使用雙字母替換密碼的系統而脫穎而出,增強了電報通信的安全性。儘管惠斯通是發明者,但它自豪地承載了普萊菲爾勳爵的名字,他在推廣該密碼中發揮了重要作用。
全球採用及其在軍事戰略中的重要性
最初被英國外交部認為過於複雜,普萊菲爾密碼 在第二次布爾戰爭和第一次世界大戰等關鍵時刻在英國軍隊中獲得了廣泛的接受。到了20世紀40年代,它已被澳大利亞、德國和新西蘭等國家使用,證明了在第二次世界大戰中的重要性。
現代用途:教育和娛樂目的
現代計算機的出現降低了普萊菲爾密碼 的安全性及有效性。如今,它主要作為教育目的和娛樂密碼學的工具,提供了一個通往密碼技術迷人世界的入口。在這個過程中,您將:
發現普萊菲爾密碼背後的運作原理。
逐步指導如何使用普萊菲爾密碼來創建您的個性化加密密鑰。
利用我們網站的資源來嘗試驗證您的加密和解密。
普萊菲爾密碼密鑰矩陣的詳細視圖
理解希爾密碼:一個全面的指南
希爾密碼 ,由萊斯特·S·希爾在1929年設計的關鍵加密技術,在經典密碼學領域因其獨特應用線性代數 和矩陣理論 而與眾不同。與其前身不同,希爾密碼採用矩陣乘法進行加密,要求密鑰:一個矩陣,對演算法有效運行必須是可逆的。
這種高級密碼技術 將字母塊作為單個單元加密,提高了其複雜性,並使其從傳統的替代密碼中顯著脫穎而出。下面,我們將深入探討希爾密碼的數學基礎和操作機制:
字符的矩陣表示: 為字母分配數值(例如,A=0, B=1, ..., Z=25)並將資訊分成塊,表示為n維向量。密鑰矩陣: 一個必須在模26下可逆的n x n矩陣,以確保可解密性。加密過程: 涉及將密鑰矩陣與明文塊向量相乘,模26。解密過程: 通過乘以密鑰矩陣的逆矩陣與加密向量相乘,模26來實現。
希爾密碼的安全性主要依賴於執行模26的矩陣逆轉的複雜性。然而,它仍然容易受到已知明文攻擊,並且需要調整明文長度以匹配矩陣大小,通常需要額外的填充。
儘管存在這些漏洞,希爾密碼仍因其在傳播密碼學基礎知識方面的教育價值而受到讚揚。雖然它在現代應用中的實際用途可能有限,但它在密碼學教育和研究中是依舊是一個關鍵的墊腳石。
學習成果:
掌握希爾密碼的工作原理及其加密步驟。
學習希爾密碼在加密和解密訊息中的應用。
理解線性代數和矩陣理論在希爾密碼中的核心作用。
明白希爾密碼和普萊菲爾密碼之間的區別。
了解四方密碼:密碼學歷史的關鍵
密碼的定義
Félix Delastelle 在他的書 Traité Élémentaire de Cryptographie 中提供了以下定義:
On appelle cryptographie la science qui a pour objet l'étude des moyens susceptibles d'assurer le secret des correspondances ou écrits qu'on a intérêt à soustraire à la curiosité des tiers ou à l'indiscrétion des intermédiaires. En d'autres termes, la cryptographie enseigne à transformer un langage clair en langage secret.
Delastelle 強調,密碼學是一門科學而非藝術。他認為,加密在給定特定方法和密鑰時,會生成一個獨特的明文版本,類似於算術運算。這突顯了密碼過程的結構化和科學性,與解密的解釋性和可變性形成對比。
四方密碼的工作原理
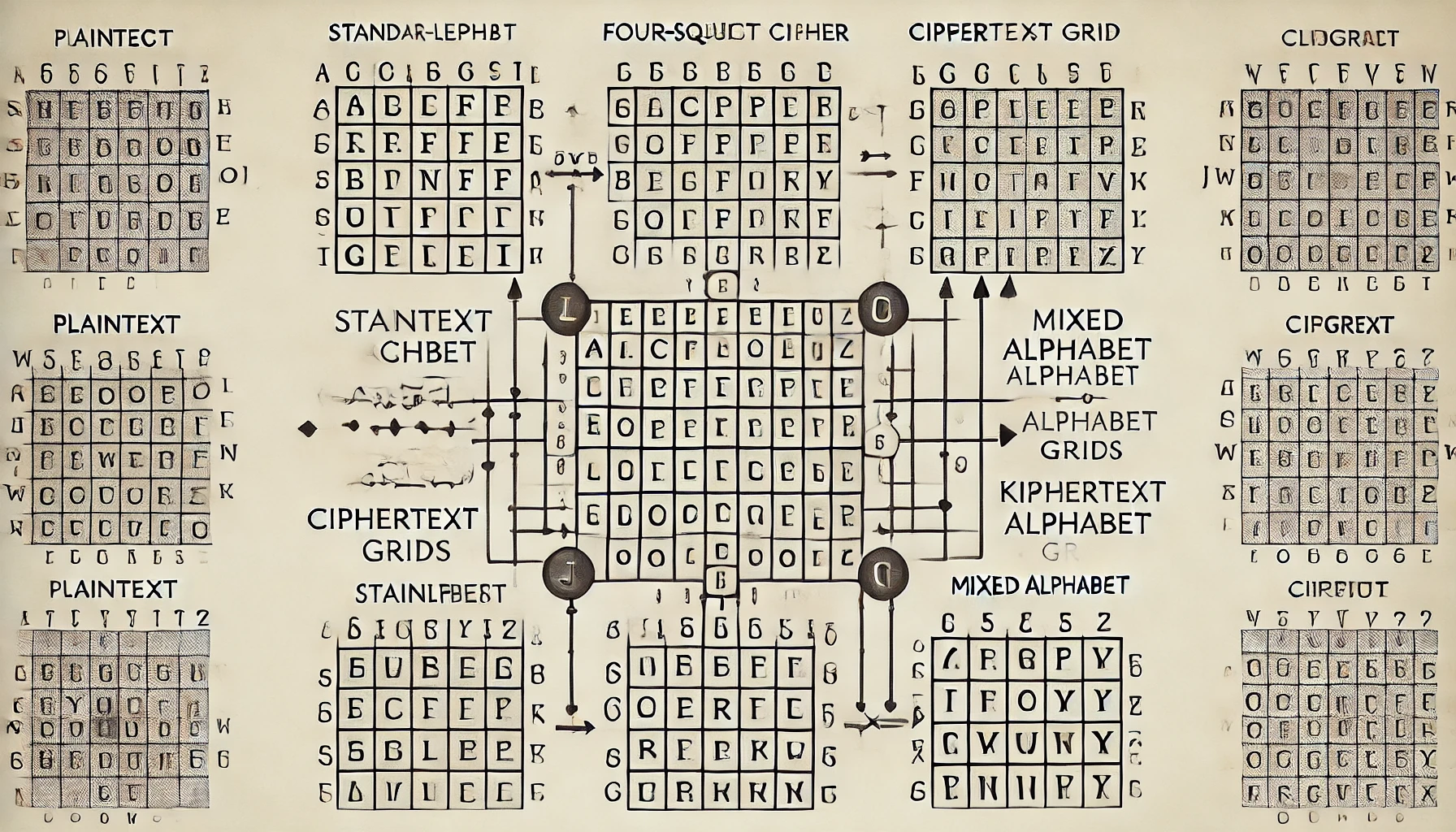
四方密碼 使用四個5x5矩陣來加密二聯字。以下是密碼工作原理的詳細分解:
準備: 創建四個5x5的方格(網格)。左上角和右下角的方格包含標準字母表(去掉'J'以適應25個字母)。右上角和左下角的方格用混合或基於關鍵字的字母表填充。這些混合字母對於密碼的安全性至關重要。
加密二聯字:
步驟1: 將明文消息分成二聯字(字母對)。如果字母數量是奇數,則添加一個額外的字母,如'X',以完成最後一對。
步驟2: 對於每個二聯字,在左上方格中找到第一個字母,在右下方格中找到第二個字母。
步驟3: 確定這些字母在各自方格中的坐標(行和列)。
步驟4: 使用這些坐標在右上方格和左下方格中找到對應的字母。在右上方格中,與第一個明文字母在同一行但在第二個明文字母的列中的字母成為密文二聯字的第一個字母。同樣,在左下方格中,與第二個明文字母在同一行但在第一個明文字母的列中的字母成為密文二聯字的第二個字母。
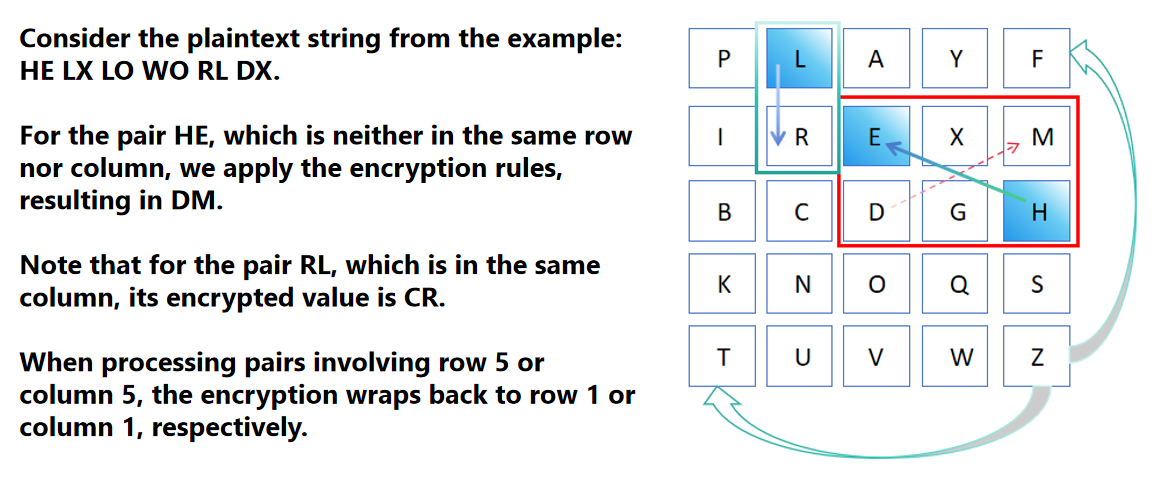
示例: 加密二聯字"HI"。
步驟1: 在左上方格中找到'H',在右下方格中找到'I'。假設'H'位於左上方格的第2行第3列,'I'位於右下方格的第3行第4列。
步驟2: 在混合字母表中找到這些坐標上的字母。在右上方格中,找到第2行第4列的字母。在左下方格中,找到第3行第3列的字母。
步驟3: 將這些字母組合形成密文二聯字。
解密: 解密過程涉及反向這些步驟。接收者必須知道方格的排列和使用的混合字母。通過在右上方格和左下方格中找到密文字母並將其映射回左上方格和右下方格中的對應明文字母,可以重建原始消息。
四方密碼加密示意圖
通過瀏覽頁面,您將學習到:
了解四方密碼的作者及其作品
掌握四方密碼的加密和解密原理
使用網頁上提供的工具嘗試自己進行加密和解密
此外,通過閱讀 Traité Élémentaire de Cryptographie ,您將對密碼學有更深入的了解。通過互動教程和示例,您將深入探討這種經典加密方法的複雜性和魅力。
加密技術的真正魅力在於它體現了人類對自由和隱私不懈追求的象徵。在這個建立在資料之上的世界裡,
它提醒我們,儘管面臨著無數挑戰,只要我們擁有智慧和勇氣,就能在數字時代保護我們最珍貴的寶藏。