Hash Value Test
Enter text to view the process of converting it into a hash value in real-time,
or select a file to calculate the file's hash value.
Generate Text Hash Value
Compare Text Hash Value
Generate File Hash Value
Compare File Hash Value
Input Hash Value 1
Input Hash Value 2
"In today's digital age, data security is not only the cornerstone of protecting personal privacy and corporate secrets but also the key to maintaining social trust and economic stability."
What is a Hash Value?
A hash value is a fixed-size string or number generated from any size of input data by a hash function. These functions accept diverse inputs like text, images, and videos, producing a fixed-length, irreversible hash value. Hash values are deterministic, meaning identical inputs always result in the same output. They also feature collision resistance, making it challenging to find distinct inputs that yield the same output.
Functions of Hash Value
Hash values serve essential roles across computer science and IT, offering a fixed-length summary of data regardless of size. These functions facilitate various applications:
- Data Integrity Verification: Used to check if data remains unmodified during transmission, ensuring the integrity of downloaded files.
- Password Storage: Passwords are stored as hash values for security, making it difficult to recover original passwords from compromised databases.
- Fast Data Retrieval: Hash values act as indices in hash tables, allowing for efficient data operations.
- Data Deduplication: Helps in identifying and removing duplicate data items by comparing hash values.
- Digital Signature and Verification: Ensures data integrity and origin through public key cryptography and hash functions.
- Blockchain Technology: Utilizes hash values to secure transaction records and ensure data immutability.
- Tamper-Proof Timestamps: Provides an irreversible timestamp for data, useful in legal and copyright protections.
The reason hash values are effective in these areas is due to their key characteristics of speed, determinism, irreversibility, and collision resistance. Properly utilized, hash functions can provide robust support in securing data, enhancing efficiency, and verifying the authenticity of information.
What is a Hash function?
A hash function is a mathematical construct that maps input data (or "message") to a fixed-size string, typically a numerical value, as illustrated in the diagram below. Widely utilized in data management and information security, a hash function is characterized by its efficient computational performance, consistent output length, irreversibility, sensitivity to input variations, and collision resistance.

Efficient Computational Performance
Hash functions can quickly calculate hash values from data of any form, regardless of the size of the data. This characteristic is crucial for applications that require fast access to data, such as hash tables. This is because, when storing data in hash tables, the speed of the hash function determines the speed of data retrieval. Hash tables use hash functions to quickly locate the storage location of the data, relying on the fast computational ability of hash functions.
Moreover, in systems that need to process large amounts of data, the efficiency of hash functions directly impacts the overall system performance. If a hash function runs slowly, it will become a bottleneck in system performance. Some real-time systems, such as packet filtering in network devices, require immediate computation of hash values for data to make quick decisions. In these cases, the efficiency of hash functions is equally crucial.
For example, consider an online e-commerce platform where users might enter product names in the search bar to find products. The backend system may use hash functions to quickly locate product information stored in hash tables. If the hash function calculation process is slow, user experience will be severely affected, as they will have to wait longer to get search results. In this situation, the efficient computational performance of hash functions ensures fast response times, thereby improving user experience. [Learn More]
Output Length Consistency in Hash Functions
Hash functions convert input of any length into a fixed-length output through a complex series of calculations. This process often involves dividing the input data into fixed-size blocks (for those inputs exceeding the size of the processing unit), applying a series of mathematical and logical operations to each block, and then combining or accumulating the results of these operations in some way to ultimately produce a fixed-size hash value.
Why is it important? The consistency of output length helps ensure the security of hash functions. If the length of the hash output could vary, it might leak information about the size of the original data, which could potentially be exploited to attack the system in some scenarios. Moreover, a fixed output length also makes it difficult for attackers to infer characteristics of the input data by analyzing the output length. At the same time, fixed-length outputs simplify the storage and comparison of hash values. System designers can know in advance how much space each hash value will occupy, which is very important for scenarios such as database design and network transmission. Furthermore, the consistency of output length becomes very efficient for comparing whether hash values are equal because it only requires comparing data of a fixed length. This is particularly important when using hash tables for fast data retrieval.
Taking SHA-256 as an example, this widely used cryptographic hash function always produces a 256-bit (i.e., 32-byte) hash value, regardless of whether the input data is a single byte or several million bytes. This consistency ensures that SHA-256 hash values can be used for various security applications, such as digital signatures and Message Authentication Codes (MACs), while simplifying the data processing and storage workflow.
Irreversibility of Hash Functions
Hash functions are unidirectional, meaning that it is impossible to infer the original data from the hash value. This characteristic is particularly important when storing passwords, as even if the database is compromised, attackers cannot recover the passwords from the hash values. The irreversibility of hash functions is mainly based on the following principles and characteristics:
- Compression: Hash functions can map inputs of any length (which might be very large in practical use) to a fixed-length output. This means there are infinitely many possible inputs mapped to a finite number of outputs. Since the output space (hash values) is much smaller than the input space, different inputs will inevitably produce the same output, a phenomenon known as a "collision." Due to this compression, it is impossible to determine the specific input from a given output (hash value).
- High Non-linearity and Complexity: Hash functions are designed using complex mathematical and logical operations (such as bitwise operations, modulo operations, etc.), to ensure that the output is highly sensitive to the input. Even minor changes to the input (for example, changing one bit) can cause significant and unpredictable changes to the output (hash value). This high degree of non-linearity and the randomness of the output make it extremely difficult to deduce the original input from the hash value.
- Unidirectionality: The design of hash functions ensures that their operation is one-way; that is, while computing the hash value is easy, the reverse process (recovering the original data from the hash value) is not feasible. This is because the computation process of hash functions involves a series of irreversible operations (such as the irreversibility of modulo operations), ensuring that even with the hash value, it is impossible to reverse-engineer the original data.
- Random Mapping: An ideal hash function should act as a "random mapper," meaning that every possible input is equally likely to be mapped to any point in the output space. This property ensures there is no feasible way to predict which output a specific input will map to, enhancing the irreversibility of the hash function.
- Mathematical Foundation: Mathematically, the irreversibility of hash functions can be understood through their reliance on "discrete logarithm problems," "large integer factorization problems," or other number theory problems that are difficult to solve with current mathematical and computational capabilities. For example, the design of some hash algorithms may indirectly depend on the computational difficulty of these problems, thereby ensuring their irreversibility.
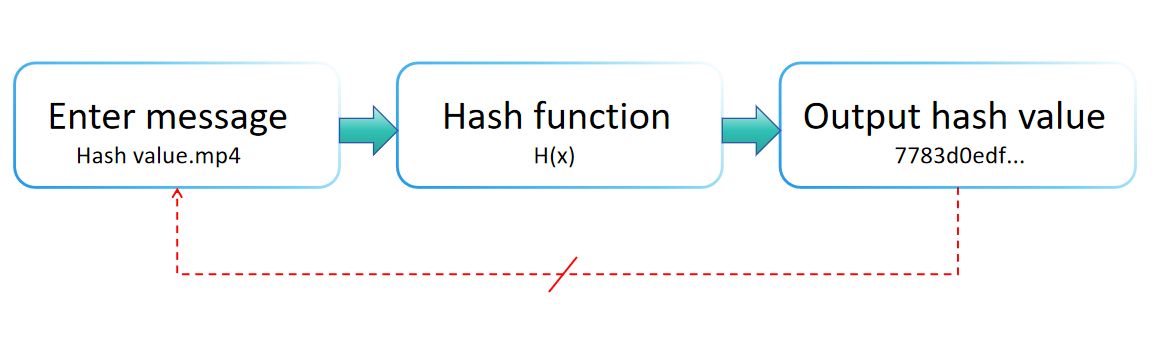
Input Sensitivity and the Avalanche Effect
In the design of hash functions, complex mathematical and logical operations (such as bitwise operations, modulo operations, etc.) are utilized to ensure that the output is highly sensitive to the input. Even minor changes to the input (for example, changing a single bit) will result in significant and unpredictable changes in the output (the hash value), a phenomenon known as the “avalanche effect”. [Learn More]
Collision Resistance in Cryptography
The collision resistance of a hash function is a crucial concept in cryptography, indicating the security level of a hash function against collision attacks. This property implies that for any hash function H, finding two distinct inputs x and y (x ≠ y) such that H(x) = H(y) is computationally infeasible. A hash function with robust collision resistance makes it extremely challenging to find two different inputs leading to the same output value.
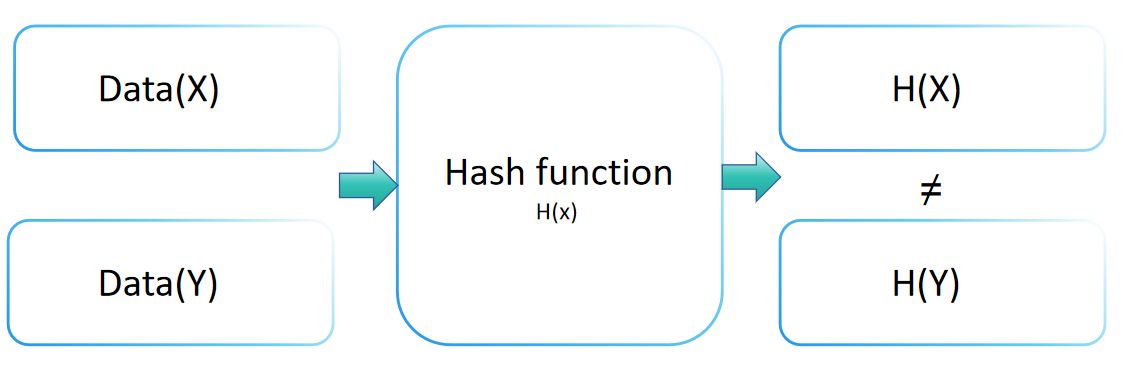
Collision resistance plays a vital role in maintaining data integrity and verification. By transforming input information into a fixed-size output (or digest), hash functions ensure that no two different inputs produce the same output. This unique characteristic allows the hash value to identify the original value accurately.
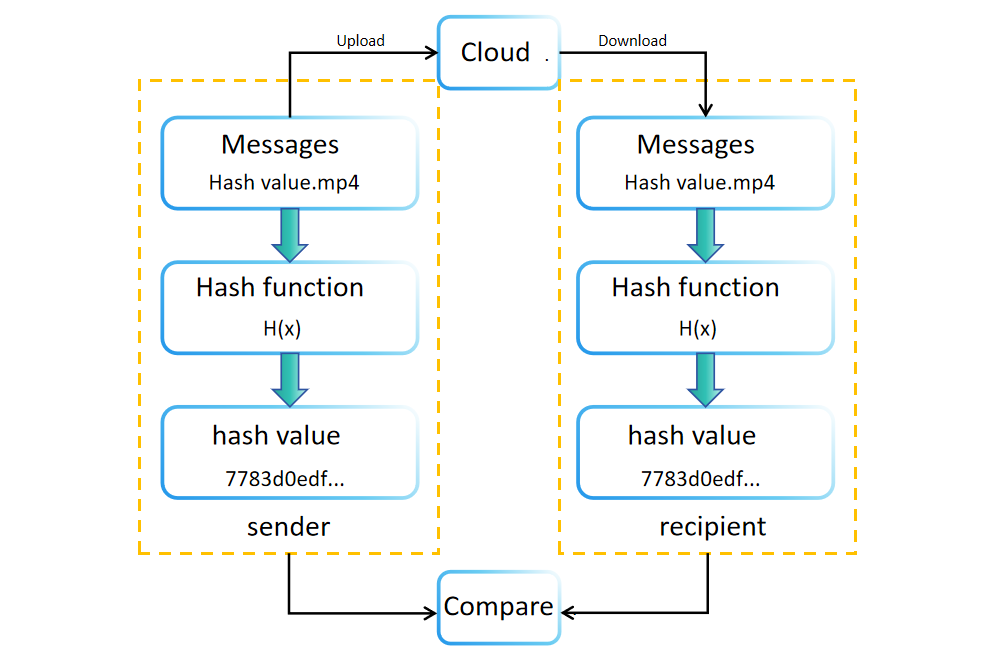
During data creation or storage, a hash value (or digest) is generated using a hash function. This value is stored or transmitted alongside the original data. For instance, software download sites often display file hash values for integrity verification. Recipients can independently recalculate the received data's hash value to confirm its integrity. If the original and recalculated hash values match, the data's integrity is verified. If not, the data may have been tampered with or corrupted during transmission or storage.
Comparing hash values also offers the advantage of verifying data integrity without requiring significant storage space. This method allows recipients to confirm data authenticity by simply comparing hash values before and after transmission.
Can hash collisions be found?
Through the characteristics of the hash functions mentioned above, we have understood collision resistance. But is it possible for hash collisions to exist, that is, for two different inputs to produce the same output? The answer is affirmative, collisions indeed exist. According to the pigeonhole principle, as long as the input space is sufficiently large, there is a possibility of hash collisions. This is because the output space of hash functions is usually much smaller than the input space, inevitably leading to multiple different inputs mapping to the same output.
The pigeonhole principle is a simple and intuitive principle of combinatorial mathematics, stating that if more than n objects are placed into n containers, then at least one container will contain two or more objects. This principle can also be used to explain problems such as the birthday paradox.
The application of the pigeonhole principle is very broad, with important uses in fields such as cryptography, computer science, and mathematics. For example, in computer science, the pigeonhole principle is used to prove the correctness of certain algorithms or to analyze the time complexity of algorithms. In cryptography, the pigeonhole principle is also used to design certain cryptographic attack methods, such as the birthday attack.
The birthday paradox is a classic application of the pigeonhole principle. Suppose there are n people in a room. If we want the probability that at least two people share the same birthday to be greater than 50%, how many people are needed? According to the pigeonhole principle, if 367 people (assuming there are 366 days in a year, plus an extra day for February 29 in a leap year) are placed into 366 "pigeonholes" (i.e., birthdays), then at least one "pigeonhole" will contain two people, meaning at least two people share the same birthday. This illustrates the birthday paradox.
It is important to note that, although the pigeonhole principle is simple and intuitive, its application must consider the specific context. For instance, when applying the pigeonhole principle, it is necessary to ensure that the random variables involved are independent of each other; otherwise, it may lead to incorrect conclusions. Moreover, in some cases, it is also necessary to consider factors such as the size and shape of the pigeonholes.
However, attempting to find hash collisions by simply traversing the input space may not be practical, mainly for two reasons:
- Computational complexity: For most hash functions, the input space is vast. Take SHA-256 as an example; its output is a 256-bit hash value, which means it has 2^256 possible outputs. Since one of the design goals of hash functions is to minimize collisions as much as possible, theoretically, finding a hash collision for SHA-256 would require traversing about 2^(256/2) = 2^128 inputs, according to the birthday paradox, which is the approximate expected number of inputs to find a collision. Even with the most powerful supercomputers currently available, it would take far beyond a human lifetime to complete such a task. making it considered impossible to find a SHA-256 hash collision through simple traversal.
- Design of hash functions: Hash functions are typically designed to make finding collisions computationally infeasible. This means that, although collisions theoretically exist, they are practically impossible to find in practice. This is an important characteristic of cryptographic hash functions (such as SHA-256), which are widely used in areas such as digital signatures, password storage, and more.
Of course, we can also use specific algorithms to try to find hash collisions. These algorithms often exploit some known properties or weaknesses of hash functions to find collisions. Here are some common techniques and methods for finding hash collisions:
- Birthday Attack: This is a probability-based simple method used to estimate the time required to find a collision when inputs are randomly chosen. The principle of the birthday attack is that if there are many people in a room, the probability of two people having the same birthday increases with the number of people. Similarly, in hash functions, if a sufficient number of inputs are randomly selected, it's likely that two inputs will eventually produce the same hash output.
- Brute Force Attack: This is the most straightforward method, which involves traversing all possible inputs to find a collision. However, this method is impractical for hash functions with large input spaces due to the enormous computational resources and time required.
- Rainbow Tables: This technique is used to pre-compute and store a large number of hash values and their corresponding inputs. Rainbow tables are especially useful for cracking passwords that have not used random data obfuscation or have a known hash function. By looking up in the rainbow table, an attacker can quickly find an input that matches a specific hash value.
- Hash Extension Attacks: Certain hash functions allow attackers to combine additional data with a known hash value without knowing the original input, thereby generating a new hash value. This attack can be used to construct collisions or perform other types of attacks.
- Specially Constructed Inputs: Sometimes, attackers can exploit specific weaknesses or non-linear behaviors in hash functions to construct special inputs that are more likely to produce collisions in the hash function.
What are the commonly used hash functions?
MD5 (Message Digest Algorithm 5)
MD5 is a widely used cryptographic hash function, designed by Ronald Rivest in the 1990s to replace the older MD4 algorithm. It can convert a message of any length into a fixed-length hash value (128 bits, or 16 bytes).
The design goal of MD5 was to provide a fast and relatively secure way to generate a digital fingerprint of data. However, collision methods for MD5 have been discovered, rendering the algorithm insecure, but it is still widely used in situations where security is not a primary concern.
The calculation process of MD5 involves the following steps:
- Padding: Initially,the original data is padded so that its byte length is a multiple of 512. The padding starts with a 1, followed by 0s until the length requirement is met.
- Adding Length: A 64-bit length value, which is the binary representation of the original message length, is added to the padded message, making the final message length a multiple of 512 bits.
- Initializing the MD Buffer: Four 32-bit registers (A, B, C, D) are initialized to store the intermediate and final hash values.
- Processing Message Blocks: The padded and length-processed message is divided into 512-bit blocks, and each block is processed through four rounds of operation. Each round includes 16 similar operations based on nonlinear functions (F, G, H, I), left circular shift operations, and addition modulo 32.
- Output: The final hash value is the content of the last state of the four registers A, B, C, D concatenated together (each register is 32 bits), forming a 128-bit hash value.
SHA-1 (Secure Hash Algorithm 1)
SHA-1 was designed by the United States National Security Agency (NSA) and released as a Federal Information Processing Standard (FIPS PUB 180-1) by the National Institute of Standards and Technology (NIST) in 1995.
SHA-1 is intended for use in digital signatures and other cryptographic applications, generating a 160-bit (20-byte) hash value known as a message digest. Although it is now known that SHA-1 has security vulnerabilities and has been superseded by more secure algorithms such as SHA-256 and SHA-3,
understanding its working principle still holds educational and historical value.
The design purpose of SHA-1 is to take a message of arbitrary length and produce a 160-bit message digest to verify the integrity of the data. Its computation process can be divided into the following steps:
- Padding: Initially, the original message is padded so that its length (in bits) modulo 512 equals 448. The padding always starts with a "1" bit, followed by several "0" bits, until the above length condition is met.
- Adding Length: A 64-bit block is added to the padded message, representing the length of the original message (in bits), making the final message length a multiple of 512 bits.
- Initializing Buffer: The SHA-1 algorithm uses a 160-bit buffer, divided into five 32-bit registers (A, B, C, D, E), to store the intermediate and final hash values. These registers are initialized to specific constant values at the beginning of the algorithm.
- Processing Message Blocks: The pre-processed message is divided into 512-bit blocks. For each block, the algorithm executes a main loop containing 80 similar steps. These 80 steps are divided into four rounds, each with 20 steps. Each step uses a different nonlinear function (F, G, H, I) and a constant (K). These functions are designed to increase the complexity and security of the operations.In these steps, the algorithm uses bitwise operations (such as AND, OR, XOR, NOT) and addition modulo 32, as well as left circular shifts.
- Output: After processing all blocks, the accumulated values in the five registers are concatenated to form the final 160-bit hash value.
SHA-2 (Secure Hash Algorithm 2)
SHA-2 is a family of cryptographic hash functions, including several different versions, primarily consisting of six variants: SHA-224, SHA-256, SHA-384, SHA-512, SHA-512/224, and SHA-512/256.
SHA-2 was designed by the United States National Security Agency (NSA) and published as a Federal Information Processing Standard (FIPS) by the National Institute of Standards and Technology (NIST). Compared to its predecessor, SHA-1, SHA-2 offers enhanced security, mainly reflected in longer hash values and stronger resistance to collision attacks.
The operation of the SHA-2 family is similar to SHA-1 in many aspects but provides higher security through the use of longer hash values and a more complex processing procedure. Here are the main steps of the SHA-2 algorithm:
- Padding: The input message is first padded to make its length, minus 64 bits, equal to 448 or 896 on a modulo 512 (for SHA-224 and SHA-256) or modulo 1024 (for SHA-384 and SHA-512) basis. The padding method is the same as SHA-1, which involves adding a "1" at the end of the message, followed by several "0"s, and finally a 64-bit (for SHA-224 and SHA-256) or 128-bit (for SHA-384 and SHA-512) binary representation of the original message length in bits.
- Initializing Buffer: The SHA-2 algorithm uses a set of initialized hash values as the starting buffer, depending on the chosen SHA-2 variant. For example, SHA-256 uses eight 32-bit registers, while SHA-512 uses eight 64-bit registers. These registers are initialized to specific constant values.
- Processing Message Blocks: The padded message is divided into 512-bit or 1024-bit blocks, and each block undergoes multiple rounds of cryptographic operations. SHA-256 and SHA-224 perform 64 rounds of operations, while SHA-512, SHA-384, SHA-512/224, and SHA-512/256 perform 80 rounds.Each round of operation includes a series of complex bitwise operations, including logical, modular addition, and conditional operations, relying on different nonlinear functions and predefined constants. These operations increase the complexity and security of the algorithm.
- Output: Finally, after processing all blocks, the values in the buffer are combined to form the final hash value. Depending on the SHA-2 variant, this hash value can be 224, 256, 384, or 512 bits long.
You might be curious as to why the input to a hash function can be of arbitrary length, but the output is fixed. The reason is that the SHA-2 family uses the Merkle-Damgård transformation, which allows for the construction of hash functions that can process messages of any length from a compression function of fixed length. The Merkle-Damgård transformation is adopted in many traditional hash functions, including MD5 and SHA-1.
The core idea of the Merkle-Damgård transformation is to divide the input message into fixed-size blocks and then process these blocks one by one, with each processing step depending on the result of the previous one, ultimately producing a fixed-size hash value. The padding step of SHA-256 embodies the basic principles of the Merkle-Damgård transformation, namely, by appropriately padding to process messages of any length and ensuring that the final processed message length meets certain conditions (such as being a multiple of a fixed length). Therefore, it can be said that the padding step of SHA-256 follows the Merkle-Damgård transformation method.
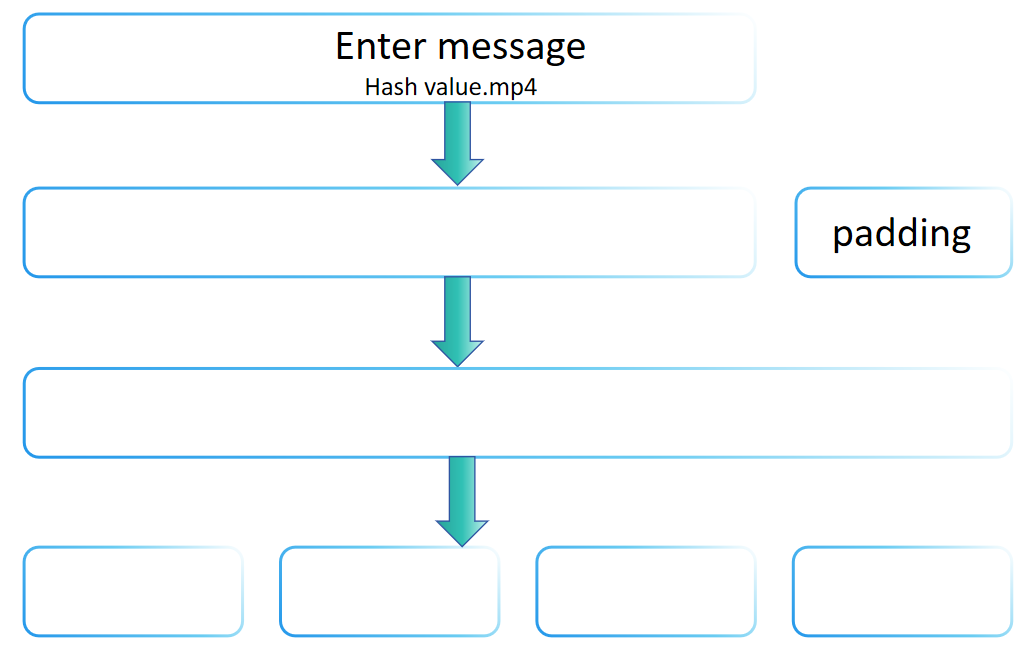
However, SHA-256 is not merely a direct implementation of the Merkle-Damgård transformation. It also includes a series of complex computational steps (such as message expansion, multiple rounds of compression functions, etc.), which are unique designs of SHA-256, aimed at enhancing its security. Therefore, although SHA-256 follows the principles of the Merkle-Damgård transformation in its padding step, it enhances overall security by introducing other security mechanisms, making it not just limited to the basic framework of the Merkle-Damgård transformation.
SHA-3 (Secure Hash Algorithm 3)
SHA-3 is the latest secure hash standard, officially approved by the National Institute of Standards and Technology (NIST) in 2015 as a Federal Information Processing Standard (FIPS 202). SHA-3 is not intended to replace the previous SHA-1 or SHA-2 (as SHA-2 is still considered secure),
but rather to complement and offer an alternative option within the SHA family, providing a different cryptographic hash algorithm. SHA-3 is based on the Keccak algorithm, designed by Guido Bertoni and others, and was the winner of the SHA-3 competition held by NIST in 2012.
The working principle of SHA-3 significantly differs from SHA-2, mainly because it utilizes a method known as "sponge construction" to absorb and squeeze data, producing the final hash value. This method allows SHA-3 to flexibly output hash values of different lengths, thereby offering a wider range of applications than SHA-2. The main steps of SHA-3 are as follows:
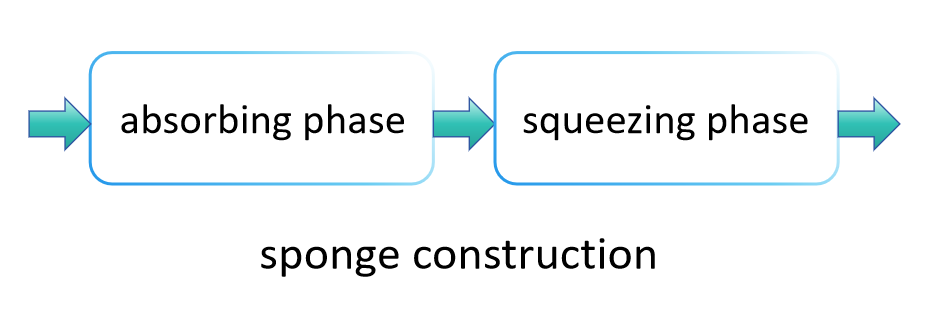
Absorbing phase:
In the absorption phase, the sponge structure first divides the input data into fixed-size blocks. These data blocks are sequentially "absorbed" into the sponge's internal state, which is typically larger than a single data block, to ensure that a large amount of data can be processed without overflow. Specifically, each data block is merged with a part of the internal state in some manner (such as by an XOR operation), followed by the application of a fixed permutation function (in SHA-3, this is Keccak-f ) to transform the entire state, thereby preventing interference between different input data blocks. This process is repeated until all input data blocks have been processed.
Keccak-f is the core permutation function used in the SHA-3 cryptographic hash algorithm. It is a central component of the Keccak algorithm family. SHA-3 is based on the Keccak algorithm, which won the cryptographic hash algorithm competition held by NIST and was selected as the standard for SHA-3. The Keccak-f function has several variants, with the most commonly used being Keccak-f[1600], where the number indicates the bit width it operates on.
Keccak-f consists of multiple rounds of the same operation (referred to as rounds). For Keccak-f[1600], there are a total of 24 rounds of operations. Each round includes five basic steps: θ (Theta), ρ (Rho), π (Pi), χ (Chi), and ι (Iota). These steps act together on the state array, gradually transforming its content, increasing confusion and diffusion to enhance security. Below is a brief description of these steps:
- θ (Theta) step: Performs XOR operations on all bits of each column, then XORs the result onto adjacent columns, providing diffusion between columns.
- ρ (Rho) step: Bit-level rotation operation, where each bit is rotated a different number of bits according to predetermined rules, increasing the complexity of the data.
- π (Pi) step: Re-arranges the bits in the state array, changing the position of the bits to achieve diffusion across rows and columns.
- χ (Chi) step: A non-linear step that performs XOR operations on each bit of every row, including itself, its immediate neighbor, and the complement of the neighbor. This is a local operation that increases the non-linear characteristics of the cryptographic algorithm.
- ι (Iota) step: Introduces a round constant to part of the state array, with the constant differing in each round, to avoid having all rounds operate identically, introducing unpredictability.
Keccak-f provides a high level of security through these steps. Its design ensures that even minor changes in input lead to widespread and unpredictable changes in the state array, achieved through the principles of confusion (making it difficult for attackers to infer the input from the output) and diffusion (where minor changes in input affect multiple parts of the output).
The design of Keccak-f allows for adjustment of parameters (such as state size and number of rounds) across different security levels and application scenarios, offering great flexibility. Keccak-f[1600] is renowned for its efficient implementation, achieving high processing speeds both in hardware and in software, especially when handling large amounts of data.
Squeezing phase:
Once all the input data blocks have been absorbed into the internal state, the sponge structure enters the squeezing phase. In this stage, parts of the internal state are progressively outputted as the result of the hash function. If the required output length exceeds the amount that can be squeezed out at once, the sponge structure applies the permutation function to transform the internal state again, then continues to output more data. This process is carried on until the desired output length is reached.
The goal of SHA-3's design is to provide higher security than SHA-2 and better resistance against quantum computing attacks. Thanks to its unique sponge structure, SHA-3 is theoretically capable of resisting all currently known cryptographic attack methods, including collision attacks, preimage attacks, and second preimage attacks.
RIPEMD-160 (RACE Integrity Primitives Evaluation Message Digest)
RIPEMD-160 is a cryptographic hash function designed to provide a secure hashing algorithm. It was developed in 1996 by Hans Dobbertin and others, and it is a member of the RIPEMD (RACE Integrity Primitives Evaluation Message Digest) family.
RIPEMD-160 produces a 160-bit (20-byte) hash value, which is the origin of the "160" in its name. It is based on the design of MD4 and influenced by other hashing algorithms such as MD5 and SHA-1. RIPEMD-160 includes two parallel,
similar operations that process the input data separately and then combine the results of these two processes to generate the final hash value. This design aims to enhance security.
The computation process of RIPEMD-160 includes several basic steps: padding, block processing, and compression:
- Padding: The input message is first padded to ensure its length modulo 512 bits equals 448 bits. Padding always starts with a single bit of 1 followed by a series of 0 bits, ending with a 64-bit representation of the original message length.
- Block Processing: The padded message is divided into 512-bit blocks.
- Initialization: It uses five 32-bit registers (A, B, C, D, E), which are initialized to certain specific values.
- Compression Function: Each block is processed in turn, updating the values of these five registers through a series of complex operations. This process includes bitwise operations (such as addition, AND, OR, NOT, circular left shifts) and the use of a set of fixed constants.
- Output: After all blocks have been processed, the values of these five registers are concatenated to form the final 160-bit hash value.