हैश मूल्य क्या है?

एक हैश मूल्य एक निश्चित-आकार की स्ट्रिंग या संख्या होती है जो किसी भी आकार के इनपुट डेटा से हैश फ़ंक्शन द्वारा उत्पन्न होती है। ये फ़ंक्शन विविध इनपुट्स जैसे कि पाठ, चित्र, और वीडियो को स्वीकार करते हैं, उत्पादन में एक निश्चित-लंबाई, अपरिवर्तनीय हैश मूल्य प्रदान करते हैं। हैश मूल्य निर्धारक होते हैं, अर्थात् समान इनपुट्स हमेशा समान आउटपुट में परिणामित होते हैं। इनमें टकराव प्रतिरोध की विशेषता भी होती है, जिससे विभिन्न इनपुट्स को ढूंढना जो समान आउटपुट उत्पन्न करें, चुनौतीपूर्ण हो जाता है।

हैश मूल्य के कार्य

हैश मूल्य कंप्यूटर विज्ञान और आईटी में महत्वपूर्ण भूमिकाएँ निभाते हैं, आकार की परवाह किए बिना डेटा का एक निश्चित-लंबाई सारांश प्रदान करते हैं। ये कार्य विभिन्न अनुप्रयोगों को सुविधाजनक बनाते हैं:

• डेटा अखंडता सत्यापन: यह जाँचने के लिए प्रयुक्त होता है कि संचरण के दौरान डेटा अपरिवर्तित रहता है, डाउनलोड की गई फाइलों की अखंडता सुनिश्चित करता है।
• पासवर्ड स्टोरेज: सुरक्षा के लिए पासवर्ड हैश मूल्यों के रूप में संग्रहीत किए जाते हैं, जिससे समझौता किए गए डेटाबेस से मूल पासवर्ड की पुनः प्राप्ति कठिन हो जाती है।
• त्वरित डेटा पुनः प्राप्ति: हैश मूल्य हैश तालिकाओं में सूचकांक के रूप में कार्य करते हैं, जिससे डेटा संचालन में दक्षता आती है।
• डेटा डेडुप्लिकेशन: हैश मूल्यों की तुलना करके डुप्लिकेट डेटा आइटम्स की पहचान करने और उन्हें हटाने में मदद करता है।
• डिजिटल हस्ताक्षर और सत्यापन: सार्वजनिक कुंजी क्रिप्टोग्राफी और हैश फ़ंक्शन्स के माध्यम से डेटा की अखंडता और मूल की सुनिश्चितता करता है।
• ब्लॉकचेन प्रौद्योगिकी: लेन-देन रिकॉर्ड्स को सुरक्षित करने और डेटा की अपरिवर्तनीयता सुनिश्चित करने के लिए हैश मूल्यों का उपयोग करती है।
• टैम्पर-प्रूफ टाइमस्टैम्प्स: डेटा के लिए एक अपरिवर्तनीय टाइमस्टैम्प प्रदान करता है, जो कानूनी और कॉपीराइट सुरक्षा में उपयोगी है।

हैश मूल्य इन क्षेत्रों में प्रभावी होते हैं क्योंकि उनकी कुछ मुख्य विशेषताएं होती हैं जैसे कि गति, निश्चितता, अपरिवर्तनीयता, और टकराव प्रतिरोध। सही ढंग से उपयोग किया जाए तो, हैश फ़ंक्शन डेटा की सुरक्षा में मजबूत सहायता प्रदान कर सकते हैं, कार्यकुशलता में वृद्धि कर सकते हैं, और जानकारी की प्रामाणिकता की पुष्टि कर सकते हैं।

हैश फ़ंक्शन क्या है?

एक हैश फ़ंक्शन एक गणितीय संरचना है जो इनपुट डेटा (या "संदेश") को एक निश्चित-आकार की स्ट्रिंग में मैप करता है, आमतौर पर एक संख्यात्मक मूल्य, जैसा कि नीचे दिए गए आरेख में दर्शाया गया है। डेटा प्रबंधन और सूचना सुरक्षा में व्यापक रूप से उपयोग किया जाने वाला, एक हैश फ़ंक्शन इसकी कुशल गणनात्मक प्रदर्शन, निरंतर आउटपुट लंबाई, अपरिवर्तनीयता, इनपुट विविधताओं के प्रति संवेदनशीलता, और टकराव प्रतिरोध की विशेषताओं से परिभाषित है।

कुशल गणनात्मक प्रदर्शन

हैश फ़ंक्शन्स किसी भी रूप के डेटा से हैश मूल्यों की त्वरित गणना कर सकते हैं, चाहे डेटा का आकार कुछ भी हो। यह विशेषता उन अनुप्रयोगों के लिए महत्वपूर्ण है जिन्हें डेटा तक त्वरित पहुँच की आवश्यकता होती है, जैसे कि हैश टेबल। यह इसलिए है क्योंकि, जब हैश टेबल्स में डेटा संग्रहीत किया जाता है, तो हैश फ़ंक्शन की गति डेटा पुनःप्राप्ति की गति निर्धारित करती है। हैश टेबल्स हैश फ़ंक्शन्स का उपयोग करके डेटा के संग्रहण स्थान को त्वरित रूप से खोजते हैं, हैश फ़ंक्शन्स की त्वरित गणनात्मक क्षमता पर निर्भर करते हैं।

इसके अलावा, जिन प्रणालियों को बड़ी मात्रा में डेटा संसाधित करने की आवश्यकता होती है, उनमें हैश फ़ंक्शन्स की कार्यकुशलता सीधे तौर पर समग्र प्रणाली प्रदर्शन को प्रभावित करती है। यदि हैश फ़ंक्शन धीरे चलता है, तो यह प्रणाली प्रदर्शन में एक बाधा बन जाएगा। कुछ वास्तविक समय प्रणालियाँ, जैसे कि नेटवर्क उपकरणों में पैकेट फ़िल्टरिंग, त्वरित निर्णय लेने के लिए डेटा के हैश मूल्यों की तत्काल गणना की आवश्यकता होती है। इन मामलों में, हैश फ़ंक्शन्स की कार्यकुशलता समान रूप से महत्वपूर्ण होती है।

उदाहरण के लिए, एक ऑनलाइन ई-कॉमर्स प्लेटफॉर्म को मानें जहाँ उपयोगकर्ता उत्पादों को खोजने के लिए सर्च बार में उत्पाद नाम दर्ज कर सकते हैं। बैकएंड प्रणाली हैश फ़ंक्शन्स का उपयोग करके हैश टेबल्स में संग्रहित उत्पाद जानकारी को त्वरित रूप से खोज सकती है। यदि हैश फ़ंक्शन की गणना प्रक्रिया धीमी है, तो उपयोगकर्ता अनुभव गंभीर रूप से प्रभावित होगा, क्योंकि उन्हें सर्च परिणाम प्राप्त करने के लिए अधिक समय तक इंतजार करना पड़ेगा। इस स्थिति में, हैश फ़ंक्शन्स का कुशल गणनात्मक प्रदर्शन त्वरित प्रतिक्रिया समय सुनिश्चित करता है, जिससे उपयोगकर्ता अनुभव में सुधार होता है। [और अधिक जानें]

हैश फ़ंक्शन्स में आउटपुट लंबाई की संगति

हैश फ़ंक्शन्स किसी भी लंबाई के इनपुट को जटिल गणना की एक शृंखला के माध्यम से एक निश्चित-लंबाई के आउटपुट में परिवर्तित करते हैं। यह प्रक्रिया अक्सर इनपुट डेटा को निश्चित-आकार के ब्लॉकों में विभाजित करने में शामिल होती है (उन इनपुट्स के लिए जो प्रोसेसिंग यूनिट के आकार से अधिक होते हैं), प्रत्येक ब्लॉक पर एक शृंखला के गणितीय और तार्किक संचालन लागू करना, और फिर इन संचालनों के परिणामों को किसी तरह से संयोजित या संचित करना ताकि अंततः एक निश्चित-आकार का हैश मूल्य उत्पन्न किया जा सके।

यह महत्वपूर्ण क्यों है? आउटपुट लंबाई की स्थिरता हैश फ़ंक्शन्स की सुरक्षा सुनिश्चित करने में मदद करती है। यदि हैश आउटपुट की लंबाई भिन्न हो सकती है, तो यह मूल डेटा के आकार के बारे में जानकारी लीक कर सकती है, जिसका कुछ परिदृश्यों में प्रणाली पर हमला करने के लिए दुरुपयोग किया जा सकता है। इसके अलावा, एक निश्चित आउटपुट लंबाई यह भी मुश्किल बनाती है कि हमलावर आउटपुट लंबाई का विश्लेषण करके इनपुट डेटा की विशेषताओं का अनुमान लगा सकें। साथ ही, निश्चित-लंबाई के आउटपुट्स हैश मूल्यों के संग्रहण और तुलना को सरल बनाते हैं। प्रणाली डिज़ाइनर्स पहले से जान सकते हैं कि प्रत्येक हैश मूल्य कितनी जगह लेगा, जो डेटाबेस डिज़ाइन और नेटवर्क ट्रांसमिशन जैसे परिदृश्यों के लिए बहुत महत्वपूर्ण है। इसके अलावा, आउटपुट लंबाई की स्थिरता हैश मूल्यों की समानता की तुलना करने में बहुत कुशल बन जाती है क्योंकि इसमें केवल निश्चित लंबाई के डेटा की तुलना करनी होती है। यह विशेष रूप से महत्वपूर्ण है जब हैश टेबल्स का उपयोग त्वरित डेटा पुनःप्राप्ति के लिए किया जाता है।

एक उदाहरण के रूप में SHA-256 को लेते हुए, यह व्यापक रूप से प्रयोग किया जाने वाला एन्क्रिप्टेड हैश फ़ंक्शन हमेशा एक 256-बिट (यानी, 32-बाइट) हैश मान उत्पन्न करता है, चाहे डाटा एकल बाइट हो या कई मिलियन बाइट। यह सततता सुनिश्चित करती है कि SHA-256 हैश मानों का उपयोग विभिन्न सुरक्षा एप्लिकेशनों के लिए किया जा सकता है, जैसे डिजिटल साइनेचर और संदेश प्रमाणीकरण कोड (MACs), जबकि डेटा प्रोसेसिंग और स्टोरेज वर्कफ़्लो को सरल बनाने में मदद करती है।

हैश फ़ंक्शन की अप्रतिवर्तीता

हैश फ़ंक्शन एकदिशीय होते हैं, जिसका अर्थ है कि हैश मूल डेटा को से नहीं पता लगाया जा सकता। यह विशेषता विशेष रूप से पासवर्ड स्टोर करते समय महत्वपूर्ण होती है, क्योंकि यदि डेटाबेस को कम्प्रोमाइज़ किया जाता है, तो हमलावर हैश मूल्यों से पासवर्ड को पुनः प्राप्त नहीं कर सकते। हैश फ़ंक्शन की अप्रतिवर्तीता मुख्य रूप से निम्नलिखित सिद्धांतों और विशेषताओं पर आधारित है:

• संक्षेपण: हैश फ़ंक्शन किसी भी लंबाई के इनपुट को (जो व्यावहारिक उपयोग में बहुत बड़ी हो सकती है) एक निश्चित-लंबाई आउटपुट में मैप कर सकते हैं। इसका अर्थ है कि निश्चित-लंबाई आउटपुट में अनंत संभावित इनपुट होते हैं। क्योंकि आउटपुट स्थान (हैश मूल्य) इनपुट स्थान से (इनपुट स्थान) काफी छोटा है, इसलिए विभिन्न इनपुट अपरिहार्य रूप से समान आउटपुट (हैश मूल्य) उत्पन्न करेंगे, जिसे "टकराव" के रूप में जाना जाता है। इस संक्षेपण के कारण, दिए गए आउटपुट (हैश मूल्य) से विशेष इनपुट (डेटा) का निश्चित पता लगाना असंभव है।
• उच्च गैर-रेखांतता और जटिलता: हैश फ़ंक्शन को जटिल गणितीय और तार्किक कार्यों (जैसे कि बिटवाइज़ कार्यों, मॉड्यूलो कार्यों, आदि) का उपयोग करके डिज़ाइन किया गया है, ताकि आउटपुट इनपुट के प्रति बहुत अधिक संवेदनशील हो। इनपुट में छोटे परिवर्तन (उदाहरण के लिए, एक बिट को बदलना) के भी महत्वपूर्ण और अप्रत्याशित परिणाम आउटपुट (हैश मूल्य) में पैदा हो सकते हैं। इस उच्च गैर-रेखांतता और आउटपुट की असमानता के लिए अप्रतिवर्तीता बनाने की बड़ी डिग्री और उत्प्रेरक अनुमानित और परिवर्तनशील बनाते हैं।
• एकदिशीयता: हैश फ़ंक्शन का डिज़ाइन यह सुनिश्चित करता है कि उनका परिचालन एकदिशीय हो; अर्थात, हैश मान की गणना करना आसान है, लेकिन उलटी प्रक्रिया (हैश मान से मूल डेटा को पुनः प्राप्त करना) संभव नहीं है। यह इसलिए है क्योंकि हैश फ़ंक्शन की गणना प्रक्रिया में अपरिवर्तनीय कार्रवाईयों (जैसे कि मॉड्यूलो कार्रवाईयों की अपरिवर्तनीयता) का एक श्रृंखला शामिल होता है, जिसका अर्थ है कि हैश मूल्य के साथ भी, मूल डेटा को उलटा-पुल्टा करना संभव नहीं है।
• यादृच्छिक मैपिंग: एक आदर्श हैश फ़ंक्शन एक "यादृच्छिक मैपर" के रूप में कार्य करना चाहिए, जिसका अर्थ है कि हर संभावित इनपुट को आउटपुट स्थान में किसी भी बिंदु से मैप किया जाना समान रूप से संभव है। यह गुण यह सुनिश्चित करता है कि किस विशेष इनपुट को किस आउटपुट में मैप किया जाएगा, उसका कोई संभावित तरीका पूर्वानुमान नहीं कर सकता है, हैश फ़ंक्शन की अप्रतिवर्तीता को बढ़ाता है।
• गणितीय आधार: गणितीय रूप से, हैश फ़ंक्शन की अप्रतिवर्तीता को "विकेंद्र लघुगणना समस्याओं," "बड़े पूर्णांक घातकरण समस्याओं," या अन्य गणित नियम की समस्याओं पर निर्भर करके समझा जा सकता है जो वर्तमान गणितीय और संगणनात्मक क्षमताओं के साथ हल करना कठिन है। उदाहरण के लिए, कुछ हैश एल्गोरिदम के डिज़ाइन का प्रत्यक्ष रूप से इन समस्याओं की गणना पर निर्भरता हो सकता है, इस प्रकार उनकी अप्रतिवर्तीता की सुनिश्चिति होती है।

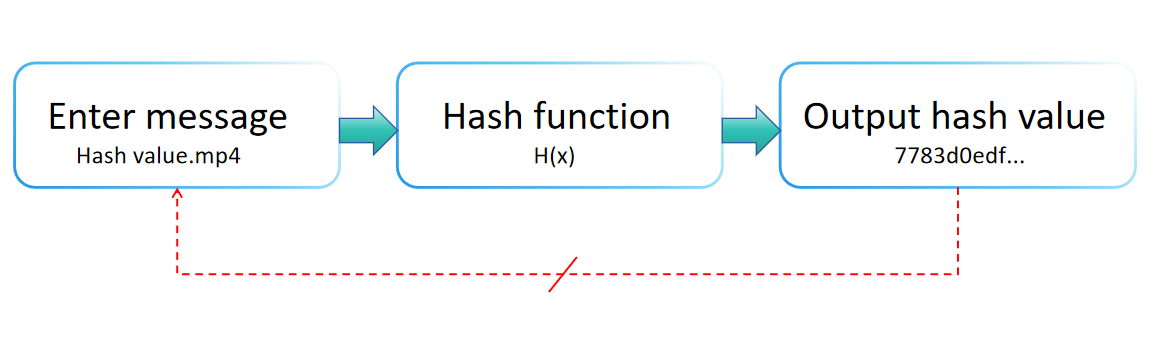
इनपुट संवेदनशीलता और बर्फानी प्रभाव

हैश फ़ंक्शन के डिज़ाइन में, जटिल गणितीय और तार्किक कार्रवाईयाँ (जैसे कि बिटवाइज़ कार्रवाईयाँ, मॉड्यूलो कार्रवाईयाँ, आदि) उपयोग की जाती हैं ताकि आउटपुट इनपुट के प्रति अत्यधिक संवेदनशील हो। इनपुट में छोटे परिवर्तन (उदाहरण के लिए, एक एकल बिट को बदलना) में आउटपुट (हैश मूल्य) में महत्वपूर्ण और अप्रत्याशित परिवर्तन होंगे, जिसे "बर्फानी प्रभाव" के रूप में जाना जाता है। [और अधिक जानें]

क्रिप्टोग्राफी में संघर्ष प्रतिरोध

हैश फ़ंक्शन का संघर्ष प्रतिरोध क्रिप्टोग्राफी में एक महत्वपूर्ण अवधारणा है, जो एक हैश फ़ंक्शन की सुरक्षा स्तर को संघर्ष हमलों के खिलाफ दर्शाता है। यह गुण इस बात का संकेत देता है कि किसी भी हैश फ़ंक्शन H के लिए, दो अलग-अलग इनपुट x और y (x ≠ y) ऐसे ढूंढना जो H(x) = H(y) हो, गणनात्मक रूप से असंभव हो। एक मजबूत संघर्ष प्रतिरोध वाला हैश फ़ंक्शन दो विभिन्न इनपुट ढूंढना बहुत ही कठिन बनाता है जो एक ही आउटपुट मान के लिए पहुंचते हैं।

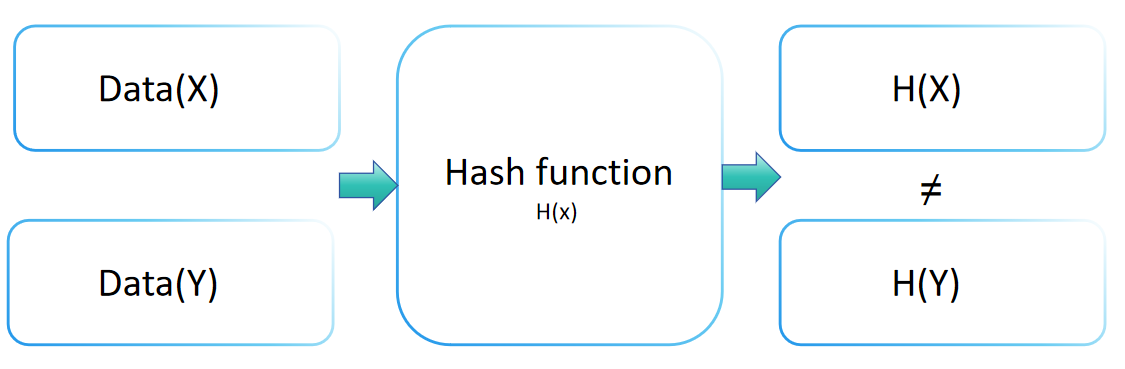
टकराव प्रतिरोध डेटा अखंडता और सत्यापन को बनाए रखने में एक महत्वपूर्ण भूमिका निभाता है। इनपुट जानकारी को एक निश्चित आकार के आउटपुट (या डाइजेस्ट) में बदलकर, हैश फंक्शन्स सुनिश्चित करते हैं कि कोई भी दो विभिन्न इनपुट एक ही आउटपुट उत्पन्न नहीं करते हैं। यह अद्वितीय विशेषता हैश मान को मूल मूल्य को सही ढंग से पहचानने की अनुमति देती है।

डेटा निर्माण या भंडारण के दौरान, एक हैश मान (या डाइजेस्ट) एक हैश फ़ंक्शन का उपयोग करके उत्पन्न किया जाता है। यह मान मूल डेटा के साथ रखा जाता है या अभिप्रेत होता है। उदाहरण के लिए, सॉफ़्टवेयर डाउनलोड साइट अक्षमता सत्यापन के लिए फ़ाइल हैश मान दिखाती हैं। प्राप्तकर्ताओं को स्वतंत्र रूप से प्राप्त डेटा का हैश मान पुनः गणना कर सकते हैं ताकि इसकी अखंडता की पुष्टि कर सकें। यदि मूल और पुनः गणना किए गए हैश मान मेल खाते हैं, तो डेटा की अखंडता सत्यापित होती है। यदि नहीं, तो डेटा को संचार या भंडारण के दौरान बदला गया हो सकता है या क्षतिग्रस्त हो सकता है।

हैश मानों की तुलना करने से डेटा अखंडता की पुष्टि करने का लाभ भी महत्वपूर्ण भंडारण स्थान की आवश्यकता के बिना होता है। इस तरीके से प्राप्तकर्ताओं को बस हैश मानों की तुलना करके डेटा की प्रामाणिकता की पुष्टि करने की अनुमति होती है, संचार के पहले और बाद में।

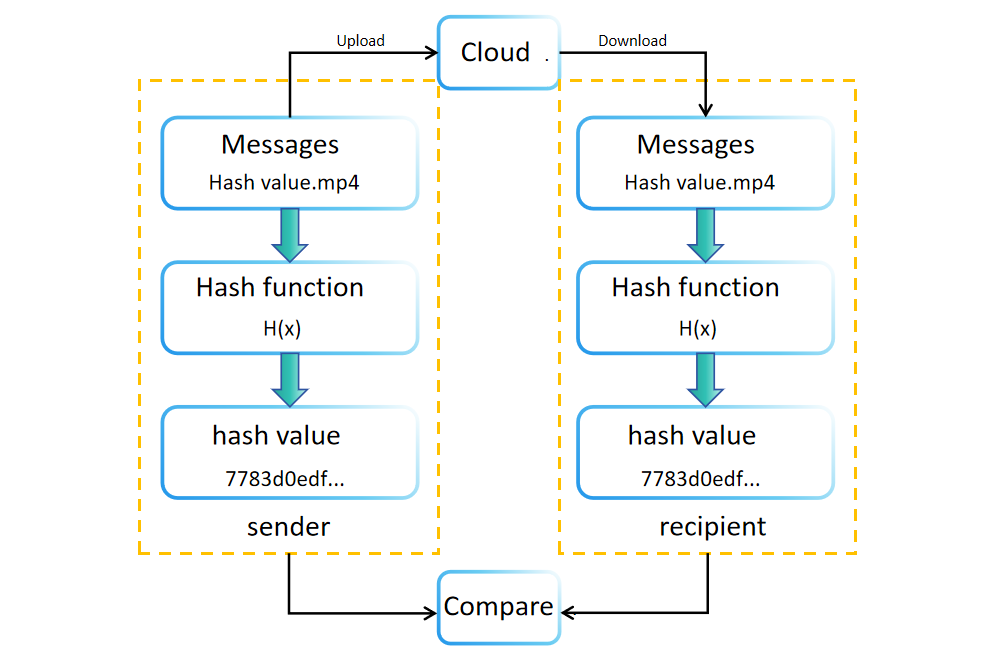
क्या हैश टकराव मिल सकते हैं?

ऊपर उल्लिखित हैश फ़ंक्शन की विशेषताओं के माध्यम से, हमने टकराव प्रतिरोध को समझ लिया है। लेकिन क्या हैश टकराव मौजूद हो सकते हैं, अर्थात, क्या दो विभिन्न इनपुट एक ही आउटपुट उत्पन्न कर सकते हैं? जवाब हाँ, टकराव वास्तव में मौजूद हैं। कबूतर-छिद्र सिद्धांत के अनुसार, जब तक इनपुट स्थान पर्याप्त बड़ा हो, हैश टकराव का संभावना होता है। इसका कारण है कि हैश फ़ंक्शन का आउटपुट स्थान सामान्यत: इनपुट स्थान से कहीं छोटा होता है, जिससे कई विभिन्न इनपुट एक ही आउटपुट में मैप हो जाते हैं।

कबूतर-छिद्र सिद्धांत एक सरल और सहज संख्यात्मक गणित का सिद्धांत है, जो कहता है कि यदि n से अधिक वस्तुएँ n कंटेनर में डाली जाती हैं, तो कम से कम एक कंटेनर में दो या दो से अधिक वस्तुएँ होंगी। यह सिद्धांत जन्मदिन पराधिर की तरह के समस्याओं का विवरण करने के लिए भी प्रयोग किया जा सकता है।

कबूतर-छिद्र सिद्धांत का उपयोग बहुत व्यापक है, जिसमें क्रिप्टोग्राफी, कंप्यूटर विज्ञान, और गणित जैसे क्षेत्रों में महत्वपूर्ण उपयोग हैं। उदाहरण के लिए, कंप्यूटर विज्ञान में, कबूतर-छिद्र सिद्धांत का उपयोग कुछ एल्गोरिदमों की सहीता को सिद्ध करने या एल्गोरिदमों की समय की परिक्षणात्मक जटिलता का विश्लेषण करने के लिए किया जाता है। क्रिप्टोग्राफी में, कबूतर-छिद्र सिद्धांत का उपयोग कुछ गुप्तशास्त्रीय हमला विधियों के डिज़ाइन में भी किया जाता है, जैसे जन्मदिन हमला।

जन्मदिन पराधिर जबरदस्ती का एक श्रेष्ठ उपयोग है कबूतर-छिद्र सिद्धांत का। मान लें कि कोई कमरे में n लोग हैं। यदि हमें कम से कम दो लोगों के बीच एक ही जन्मदिन का होने की संभावना को 50% से अधिक चाहिए, तो कितने लोगों की आवश्यकता है? कबूतर-छिद्र सिद्धांत के अनुसार, यदि 366 लोग (यहां यह मानकर कि साल में 366 दिन होते हैं, और एक अतिरिक्त दिन लीप वर्ष में फरवरी 29 का होता है) को 366 "कबूतर-छिद्र" (अर्थात, जन्मदिन) में रखा जाता है, तो कम से कम एक "कबूतर-छिद्र" दो लोगों को धारित करेगा, यानी कम से कम दो लोग एक ही जन्मदिन को मनाते हैं। यह जन्मदिन पराधिर का उदाहरण प्रस्तुत करता है।

महत्वपूर्ण बात यह है कि, हालांकि कबूतर-छिद्र सिद्धांत सरल और सहज है, इसके अनुप्रयोग को विशेष संदर्भ को ध्यान में रखना चाहिए। उदाहरण के लिए, कबूतर-छिद्र सिद्धांत का अनुप्रयोग करते समय, यह आवश्यक है कि सुनियोजित यातायात स्वतंत्र हों; अन्यथा, यह गलत नतीजों की ओर ले जा सकता है। इसके अलावा, कुछ मामलों में, कबूतर-छिद्र के आकार और आकृति जैसे कारकों को भी ध्यान में रखना आवश्यक है।

हालांकि, इनपुट स्थान को सिर्फ घूरकर हैश टकरावों को ढूंढ़ने का प्रयास सामान्यत: व्यावहारिक नहीं हो सकता, मुख्य रूप से दो कारणों के कारण:

• गणनात्मक जटिलता: अधिकांश हैश फ़ंक्शन्स के लिए, इनपुट स्थान विशाल होता है। SHA-256 को उदाहरण के रूप में लें; इसका आउटपुट एक 256-बिट हैश मान होता है, जिससे इसमें 2^256 संभावित आउटपुट होते हैं। हैश फ़ंक्शन के डिजाइन के लक्ष्यों में से एक टकरावों को जितना संभव हो सके कम करना होता है, सिद्धांतवादी रूप से, SHA-256 के लिए एक हैश टकराव खोजना करीब 2^(256/2) = 2^128 इनपुट को घूरने की आवश्यकता होगी, जो जन्मदिन पराधिर के अनुसार है, जो एक टकराव को ढूंढने के लिए अपेक्षित प्रायः संख्या होती है। वर्तमान में उपलब्ध सबसे शक्तिशाली सुपरकंप्यूटरों के साथ भी, ऐसा करने में लोगों के जीवन समय से परे हो जाएगा। जिससे यह माना जाता है कि एक ईंट की खोज निर्देशांक के माध्यम से एक SHA-256 हैश टकराव ढूंढना सरल नहीं है।
• हैश फ़ंक्शन का डिज़ाइन: हैश फ़ंक्शन्स आमतौर पर टकरावों को गणनात्मक रूप से अव्यवहार्य बनाने के लिए डिज़ाइन किए जाते हैं। इसका मतलब है कि, हालांकि सिद्धांतवादी रूप से टकराव मौजूद होते हैं, वास्तव में इन्हें अभ्यास में ढूंढना असंभव होता है। यह एक विशेषज्ञ के लिए हैश फ़ंक्शन (जैसे SHA-256) की एक महत्वपूर्ण विशेषता है, जिसे डिजिटल हस्ताक्षर, पासवर्ड संग्रहण आदि के क्षेत्र में व्यापक रूप से उपयोग किया जाता है।

बेशक, हम हैश टकरावों को ढूंढने के लिए विशिष्ट एल्गोरिदम का भी उपयोग कर सकते हैं। ये एल्गोरिदम आमतौर पर हैश फ़ंक्शन की कुछ जानी गई गुणों या कमियों का उपयोग करते हैं टकरावों को ढूंढने के लिए। यहाँ कुछ सामान्य तकनीकें और विधियाँ हैश टकरावों को खोजने के लिए:

• जन्मदिन हमला: यह एक प्रायिकता-आधारित सरल विधि है जो समय का अनुमान लगाने के लिए प्रयोग की जाती है जब इनपुट यादृच्छिक रूप से चुने जाते हैं। जन्मदिन हमले का सिद्धांत है कि अगर कमरे में बहुत से लोग होते हैं, तो दो लोगों का समान जन्मदिन होने की संभावना लोगों की संख्या के साथ बढ़ती है। इसी तरह, हैश फ़ंक्शन में, अगर पर्याप्त संख्या में इनपुट यादृच्छिक रूप से चुने जाते हैं, तो यह संभावना है कि अंततः दो इनपुट एक ही हैश आउटपुट प्रस्तुत करेंगे।
• ब्रूट फोर्स हमला: यह सबसे सीधी विधि है, जो एक टकराव ढूंढने के लिए सभी संभावित इनपुट को घूरने का समावेश करती है। हालांकि, बड़े इनपुट स्थान वाले हैश फ़ंक्शन के लिए यह विधि कार्यक्षम नहीं होती है क्योंकि इसमें भारी गणनात्मक संसाधनों और समय की आवश्यकता होती है।
• रेनबो टेबल्स: इस तकनीक का उपयोग बड़ी संख्या में हैश मानों और उनके संबंधित इनपुट्स को पूर्व-गणना करके संग्रहीत करने के लिए किया जाता है। रेनबो टेबल्स विशेष रूप से उपयोगी होते हैं उन पासवर्ड्स को क्रैक करने के लिए जिनमें यादृच्छिक डेटा अस्पष्टीकरण का उपयोग नहीं किया गया है या जिनका हैश फंक्शन ज्ञात है। रेनबो टेबल में देखकर, एक हमलावर जल्दी से एक इनपुट खोज सकता है जो एक विशिष्ट हैश मूल्य से मेल खाता है।
• हैश विस्तार हमले: कुछ हैश फ़ंक्शन्स हमलावतों को जानते हुए एक ज्ञात हैश मान के साथ अतिरिक्त डेटा को मिलाकर नया हैश मान उत्पन्न करने की अनुमति देते हैं, बिना मूल इनपुट को जाने। इस हमले का उपयोग टकराव बनाने या अन्य प्रकार के हमलों को करने के लिए किया जा सकता है।
• विशेष रूप से निर्मित इनपुट: कभी-कभी, हमलावता विशेष कमजोरियों या हैश फ़ंक्शन्स में गैर-रैखिक व्यवहारों का शोध करके विशेष इनपुट का निर्माण कर सकते हैं जो हैश फ़ंक्शन में टकराव उत्पन्न करने की संभावना होती है।

क्या हैं आमतौर पर प्रयुक्त हैश फ़ंक्शन्स?

MD5 (मैसेज डाइजेस्ट एल्गोरिदम 5)

MD5 एक व्यापकता से प्रयुक्त एन्क्रिप्टिक हैश फ़ंक्शन है, जिसे रोनाल्ड रिवेस्ट ने 1990 के दशक में पुराने MD4 एल्गोरिदम को बदलने के लिए डिज़ाइन किया था। यह किसी भी लंबाई के संदेश को एक स्थिर लंबाई के हैश मान में बदल सकता है (128 बिट्स, या 16 बाइट्स)। MD5 का डिज़ाइन लक्ष्य था डेटा का एक डिजिटल अंगुली का जल्दी और संतुलित तरीके से उत्पन्न करने के लिए एक तेज और समर्थ संरक्षित तरीका प्रदान करना। हालांकि, MD5 के लिए टकराव विधियाँ खोजी गई हैं, जिससे एल्गोरिदम असुरक्षित हो गया है, लेकिन यह अभी भी विस्तार से उपयोग किया जाता है जहां सुरक्षा प्राथमिक चिंता नहीं है।

MD5 की गणना प्रक्रिया निम्नलिखित चरणों में समाहित होती है:

• पैडिंग: प्रारंभ में, मूल डेटा को पैड किया जाता है ताकि इसकी बाइट लंबाई 512 के गुणित हो। पैडिंग एक 1 के साथ शुरू होती है, और लंबाई की आवश्यकता पूरी होने तक 0 के साथ जारी रहती है।
• लंबाई जोड़ना: पैड किए गए संदेश में मूल संदेश की बाइनरी प्रतिनिधि है जोड़ी जाती है, जिससे अंतिम संदेश की लंबाई 512 बिट के गुणित हो जाती है।
• MD बफर का प्रारंभ: चार 32-बिट रजिस्टर (A, B, C, D) को इंटरमीडिएट और अंतिम हैश मान संग्रहित करने के लिए प्रारंभिक किया जाता है।
• संदेश ब्लॉकों का प्रोसेसिंग: पैड किए गए और लंबाई-प्रोसेस्ड संदेश को 512-बिट ब्लॉक में विभाजित किया जाता है, और प्रत्येक ब्लॉक को चार दौरों के ऑपरेशन के माध्यम से प्रोसेस किया जाता है। प्रत्येक दौर में 16 असमान कार्य होते हैं जो गैर-रैखिक फ़ंक्शन (F, G, H, I), बायाँ सर्कुलर शिफ़्ट ऑपरेशन्स, और 32 के बाद जोड़ने की आवश्यकता होती है।
• आउटपुट: अंतिम हैश मान चार रजिस्टर A, B, C, D के आखिरी स्थिति की सामग्री होती है जो मिलकर एक 128-बिट हैश मान बनाती है (प्रत्येक रजिस्टर 32 बिट है),।

SHA-1 (सिक्योर हैश एल्गोरिथम 1)

SHA-1 को संयुक्त राज्य राष्ट्रीय सुरक्षा एजेंसी (NSA) द्वारा डिज़ाइन किया गया था और 1995 में राष्ट्रीय मानक संस्थान (NIST) द्वारा एक संघीय सूचना प्रक्रिया मानक (FIPS PUB 180-1) के रूप में जारी किया गया था। SHA-1 का उपयोग डिजिटल हस्ताक्षर और अन्य क्रिप्टोग्राफिक अनुप्रयोगों में किया जाता है, जो 160-बिट (20-बाइट) हैश मूल्य उत्पन्न करता है जिसे मैसेज डाइजेस्ट के रूप में जाना जाता है। हालांकि, अब यह ज्ञात है कि SHA-1 में सुरक्षा कमजोरियाँ हैं और इसे SHA-256 और SHA-3 जैसे अधिक सुरक्षित एल्गोरिथम्स द्वारा प्रतिस्थापित किया गया है, फिर भी इसके कार्य सिद्धांत को समझना शैक्षिक और ऐतिहासिक महत्व रखता है।

SHA-1 का डिज़ाइन उद्देश्य यह है कि एक मनमानी लंबाई के संदेश को लेकर एक 160-बिट मैसेज डाइजेस्ट उत्पन्न करना है ताकि डेटा की अखंडता की पुष्टि की जा सके। इसकी गणना प्रक्रिया को निम्नलिखित चरणों में विभाजित किया जा सकता है:

• पैडिंग: प्रारंभ में, मूल संदेश को ऐसे पैड किया जाता है कि इसकी लंबाई (बिट्स में) 512 के मॉड्यूलो से 448 के बराबर हो जाती है। पैडिंग हमेशा एक "1" बिट से शुरू होती है, इसके बाद कई "0" बिट्स होते हैं, जब तक कि ऊपर दी गई लंबाई की स्थिति पूरी नहीं हो जाती।
• लंबाई जोड़ना: पैड किए गए संदेश में एक 64-बिट ब्लॉक जोड़ा जाता है, जो मूल संदेश की लंबाई (बिट्स में) का प्रतिनिधित्व करता है, जिससे अंतिम संदेश की लंबाई 512 बिट्स का एक गुणक बन जाती है।
• बफर को प्रारंभ करना: SHA-1 एल्गोरिथम एक 160-बिट बफर का उपयोग करता है, जिसे पांच 32-बिट रजिस्टरों (A, B, C, D, E) में विभाजित किया गया है, जो अंतरिम और अंतिम हैश मूल्यों को स्टोर करने के लिए होते हैं। ये रजिस्टर एल्गोरिथम की शुरुआत में विशिष्ट स्थायी मानों पर आरंभ किए जाते हैं।
• संदेश ब्लॉक्स को प्रोसेस करना: प्री-प्रोसेस्ड संदेश को 512-बिट ब्लॉक्स में विभाजित किया जाता है। प्रत्येक ब्लॉक के लिए, एल्गोरिथम एक मुख्य लूप को निष्पादित करता है जिसमें 80 समान चरण होते हैं। ये 80 चरण चार राउंड में विभाजित होते हैं, प्रत्येक में 20 चरण होते हैं। प्रत्येक चरण में एक अलग गैर-रेखीय फ़ंक्शन (F, G, H, I) और एक स्थिरांक (K) का उपयोग किया जाता है। ये फ़ंक्शन ऑपरेशन्स की जटिलता और सुरक्षा बढ़ाने के लिए डिज़ाइन किए गए हैं। इन चरणों में, एल्गोरिथम बिटवाइज़ ऑपरेशन्स (जैसे कि AND, OR, XOR, NOT) और 32 के मॉड्यूलो में जोड़, साथ ही बाएँ सर्कुलर शिफ्ट्स का उपयोग करता है।
• आउटपुट: सभी ब्लॉक्स को प्रोसेस करने के बाद, पांच रजिस्टरों में संचित मूल्यों को जोड़ा जाता है ताकि अंतिम 160-बिट हैश मूल्य बनाया जा सके।

SHA-2 (सिक्योर हैश एल्गोरिथम 2)

SHA-2 एक क्रिप्टोग्राफिक हैश फंक्शन्स का परिवार है, जिसमें कई अलग-अलग संस्करण शामिल हैं, जो मुख्य रूप से छह वेरिएंट्स: SHA-224, SHA-256, SHA-384, SHA-512, SHA-512/224, और SHA-512/256 से मिलकर बना है। SHA-2 को संयुक्त राज्य राष्ट्रीय सुरक्षा एजेंसी (NSA) द्वारा डिजाइन किया गया था और राष्ट्रीय मानक संस्थान (NIST) द्वारा एक संघीय सूचना प्रक्रिया मानक (FIPS) के रूप में प्रकाशित किया गया था। इसके पूर्ववर्ती, SHA-1 की तुलना में, SHA-2 बेहतर सुरक्षा प्रदान करता है, जो मुख्य रूप से लंबी हैश मूल्यों और संघर्ष हमलों के प्रतिरोध में मजबूती से प्रतिबिंबित होता है।

SHA-2 परिवार का संचालन कई पहलुओं में SHA-1 के समान है लेकिन लंबी हैश मूल्यों और एक अधिक जटिल प्रोसेसिंग प्रक्रिया के उपयोग के माध्यम से उच्च सुरक्षा प्रदान करता है। यहाँ SHA-2 एल्गोरिथम के मुख्य चरण हैं:

• पैडिंग: इनपुट संदेश को पहले पैड किया जाता है ताकि इसकी लंबाई, 64 बिट्स को छोड़कर, 448 या 896 पर समान हो, 512 के मॉड्यूलो पर (SHA-224 और SHA-256 के लिए) या 1024 के मॉड्यूलो पर (SHA-384 और SHA-512 के लिए)। पैडिंग विधि SHA-1 के समान है, जिसमें संदेश के अंत में एक "1" जोड़ना, उसके बाद कई "0" जोड़ना, और अंत में मूल संदेश की लंबाई का 64-बिट (SHA-224 और SHA-256 के लिए) या 128-बिट (SHA-384 और SHA-512 के लिए) बाइनरी प्रतिनिधित्व शामिल है।
• बफर को प्रारंभ करना: SHA-2 एल्गोरिथम एक सेट ऑफ इनिशियलाइज़्ड हैश मूल्यों का उपयोग शुरुआती बफर के रूप में करता है, जो चुने गए SHA-2 वेरिएंट पर निर्भर करता है। उदाहरण के लिए, SHA-256 आठ 32-बिट रजिस्टरों का उपयोग करता है, जबकि SHA-512 आठ 64-बिट रजिस्टरों का उपयोग करता है। ये रजिस्टर विशिष्ट स्थिर मानों पर आरंभ किए जाते हैं।
• संदेश ब्लॉक्स को प्रोसेस करना: पैड किए गए संदेश को 512-बिट या 1024-बिट ब्लॉक्स में विभाजित किया जाता है, और प्रत्येक ब्लॉक कई राउंड्स के क्रिप्टोग्राफिक ऑपरेशन्स से गुजरता है। SHA-256 और SHA-224 64 राउंड्स के ऑपरेशन्स का प्रदर्शन करते हैं, जबकि SHA-512, SHA-384, SHA-512/224, और SHA-512/256 80 राउंड्स का प्रदर्शन करते हैं। प्रत्येक ऑपरेशन राउंड में जटिल बिटवाइज़ ऑपरेशन्स की एक शृंखला शामिल होती है, जिसमें तार्किक, मॉड्यूलर जोड़, और सशर्त ऑपरेशन्स शामिल होते हैं, जो विभिन्न गैर-रेखीय फ़ंक्शन्स और पूर्वनिर्धारित स्थिरांकों पर निर्भर करते हैं। ये ऑपरेशन्स एल्गोरिथम की जटिलता और सुरक्षा बढ़ाते हैं।
• आउटपुट: अंत में, सभी ब्लॉक्स को प्रोसेस करने के बाद, बफर में मूल्यों को मिलाकर अंतिम हैश मूल्य बनाया जाता है। SHA-2 वेरिएंट के आधार पर, यह हैश मूल्य 224, 256, 384, या 512 बिट्स लंबा हो सकता है।

आपको शायद हैरानी हो कि हैश फ़ंक्शन को क्यों बारंबार लंबाई की इनपुट दी जा सकती है, लेकिन आउटपुट फ़िक्स्ड होती है। यह कारण है कि SHA-2 परिवार में मर्कल-डामगार्ड परिवर्तन का उपयोग किया जाता है, जो हैश फ़ंक्शन का निर्माण संदेशों की किसी भी लंबाई को एक निश्चित लंबाई के संपीड़न फ़ंक्शन से प्रसंस्करण करने की अनुमति देता है। मर्कल-डामगार्ड परिवर्तन को बहुत से पारंपरिक हैश फ़ंक्शनों में अपनाया गया है, जिसमें MD5 और SHA-1 शामिल हैं।

मर्कल-डामगार्ड परिवर्तन का मूल विचार है कि इनपुट संदेश को निश्चित-साइज़ ब्लॉक में विभाजित किया जाए और फिर इन ब्लॉकों को एक के बाद एक प्रसंस्करण किया जाए, हर प्रसंस्करण कदम पिछले के परिणाम पर निर्भर करता है, अंततः एक निश्चित-साइज़ हैश मान उत्पन्न करता है। SHA-256 का पैडिंग कदम मर्कल-डामगार्ड परिवर्तन के मूल सिद्धांतों को दर्शाता है, यानी, किसी भी लंबाई के संदेश को प्रसंस्करण करने के लिए उपयुक्त तरीके से पैडिंग करके और निश्चित शर्तों (जैसे कि निश्चित लंबाई के एक गुणक का होना) को पूरा करने के लिए। इसलिए, कहा जा सकता है कि SHA-256 का पैडिंग कदम मर्कल-डामगार्ड परिवर्तन विधि का पालन करता है।

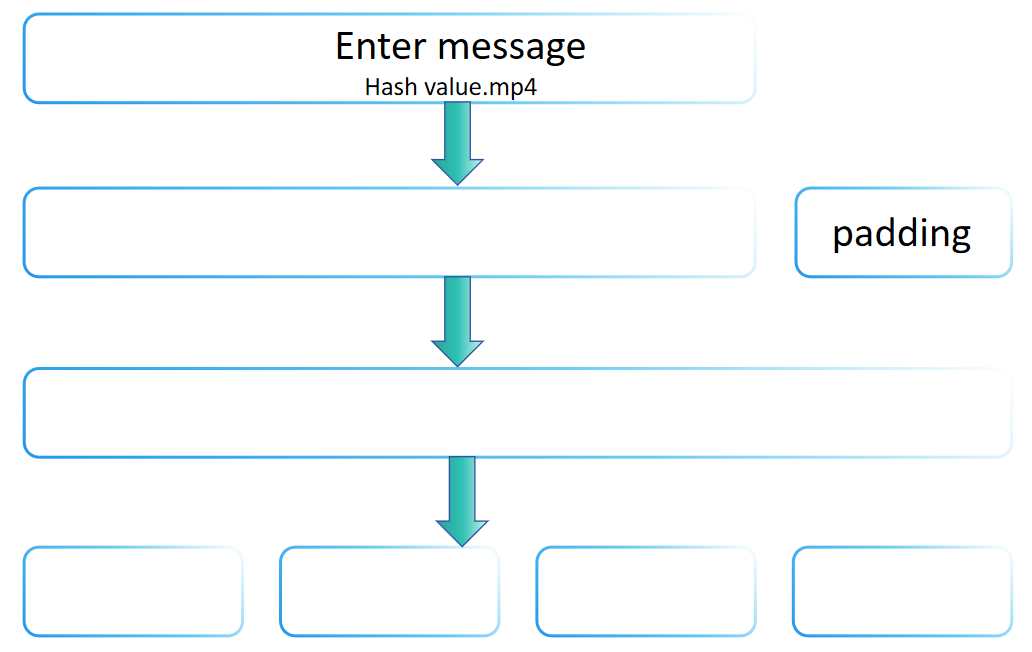
हालाँकि, SHA-256 केवल मर्कल-डामगार्ड परिवर्तन का सीधा कार्यान्वयन नहीं है। इसमें एक श्रृंखला के जटिल गणना कदम भी शामिल हैं (जैसे संदेश विस्तार, कई राउंड की संपीड़न फ़ंक्शन्स, आदि), जो एसएचए-256 के अद्वितीय डिज़ाइन हैं, जो इसकी सुरक्षा को मजबूत करने का उद्देश्य है। इसलिए, हालांकि एसएचए-256 अपने पैडिंग कदम में मर्कल-डामगार्ड परिवर्तन के सिद्धांतों का पालन करता है, यह अन्य सुरक्षा तंत्रों को परिचय कराकर समग्र सुरक्षा को मजबूत करता है, जिससे यह मर्कल-डामगार्ड परिवर्तन के मूल ढांचे से सीमित नहीं होता है।

SHA-3 (सुरक्षित हैश एल्गोरिदम 3)

SHA-3 नवीनतम सुरक्षित हैश मानक है, जो 2015 में राष्ट्रीय मानक और प्रौद्योगिकी संस्थान (NIST) द्वारा एक संघीय सूचना प्रसंस्करण मानक (FIPS 202) के रूप में आधिकारिक रूप से मंजूर किया गया था। SHA-3 का उद्देश्य पिछले SHA-1 या SHA-2 को नहीं बदलना है (क्योंकि SHA-2 अभी भी सुरक्षित माना जाता है), बल्कि SHA परिवार में एक वैकल्पिक विकल्प प्रदान करना है, जो एक विभिन्न ऊर्जावान हैश एल्गोरिदम प्रदान करता है। SHA-3 केकेक एल्गोरिदम पर आधारित है, जिसे गुईडो बर्टोनी और अन्यों ने डिज़ाइन किया था, और यह NIST द्वारा 2012 में आयोजित SHA-3 प्रतियोगिता का विजेता था।

SHA-3 का काम करने का सिद्धांत SHA-2 से प्रमुख रूप से भिन्न होता है, मुख्यतः क्योंकि इसका उपयोग "स्पंज निर्माण" नामक एक विधि का है, जो डेटा को अवशोषित और निचोड़ा गुण्जाने के लिए उपयोग किया जाता है, अंतिम हैश मान उत्पन्न करने के लिए। यह विधि SHA-3 को विभिन्न लंबाई के हैश मान लाभार्थी रूप से उत्पादित करने की अनुमति देती है, जिससे SHA-2 से अधिक आवेदन की व्यापकता प्रदान की जा सकती है। SHA-3 के मुख्य चरण निम्नलिखित हैं:

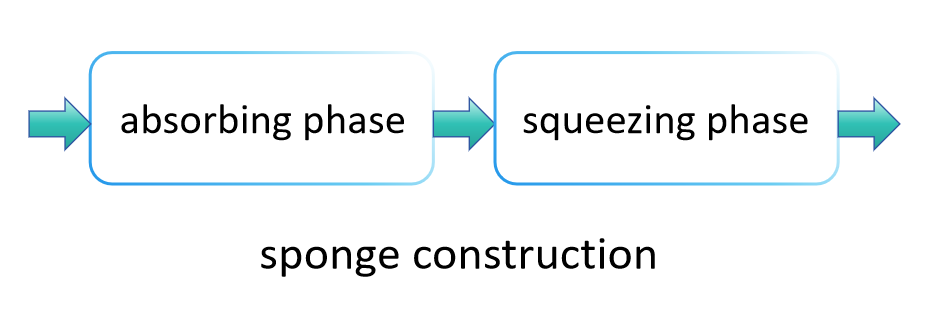
अवशोषण चरण:

अवशोषण चरण में, स्पंज संरचना पहले इनपुट डेटा को निश्चित आकार के ब्लॉक में विभाजित करती है। ये डेटा ब्लॉक क्रमिक रूप से स्पंज की आंतरिक स्थिति में "अवशोषित" किए जाते हैं, जो आम तौर पर एक एकल डेटा ब्लॉक से बड़ी होती है, ताकि बिना ओवरफ्लो के बड़ी मात्रा में डेटा को संसाधित किया जा सके। विशेष रूप से, प्रत्येक डेटा ब्लॉक को किसी प्रकार से आंतरिक स्थिति के एक हिस्से के साथ मिलाया जाता है (जैसे कि एक XOR ऑपरेशन द्वारा), इसके बाद एक निश्चित परम्युटेशन फंक्शन का आवेदन किया जाता है (SHA-3 में, यह Keccak-f है) पूरी स्थिति को परिवर्तित करने के लिए, इस प्रकार विभिन्न इनपुट डेटा ब्लॉकों के बीच हस्तक्षेप को रोकते हुए। यह प्रक्रिया तब तक दोहराई जाती है जब तक सभी इनपुट डेटा ब्लॉकों को संसाधित नहीं किया जाता।

Keccak-f SHA-3 क्रिप्टोग्राफिक हैश एल्गोरिथम में उपयोग किया जाने वाला मुख्य परिवर्तन फ़ंक्शन है। यह Keccak एल्गोरिथम परिवार का एक केंद्रीय घटक है। SHA-3 Keccak एल्गोरिथम पर आधारित है, जिसने NIST द्वारा आयोजित क्रिप्टोग्राफिक हैश एल्गोरिथम प्रतियोगिता जीती थी और SHA-3 के लिए मानक के रूप में चुना गया था। Keccak-f फंक्शन के कई वेरिएंट हैं, जिसमें सबसे अधिक प्रयुक्त Keccak-f[1600] है, जहाँ नंबर इसके ऑपरेशन पर आधारित बिट चौड़ाई को दर्शाता है।

Keccak-f एक ही ऑपरेशन के कई राउंड्स से मिलकर बनता है (जिसे राउंड्स के रूप में संदर्भित किया जाता है)। Keccak-f[1600] के लिए, कुल 24 राउंड्स के ऑपरेशन होते हैं। प्रत्येक राउंड में पाँच मूलभूत कदम शामिल होते हैं: थीटा (Theta), रो (Rho), पाई (Pi), ची (Chi), और इओटा (Iota)। ये कदम मिलकर स्थिति ऐरे पर काम करते हैं, धीरे-धीरे इसकी सामग्री को परिवर्तित करते हैं, भ्रम और प्रसार को बढ़ाकर सुरक्षा को मजबूत करते हैं। नीचे इन कदमों का संक्षिप्त वर्णन है:

• θ (Theta) कदम: प्रत्येक कॉलम के सभी बिट्स पर XOR ऑपरेशन करता है, फिर परिणाम को आसन्न कॉलमों पर XOR करता है, जिससे कॉलमों के बीच डिफ्यूजन प्रदान होता है।
• ρ (Rho) कदम: बिट-स्तरीय रोटेशन ऑपरेशन, जहाँ प्रत्येक बिट को पूर्वनिर्धारित नियमों के अनुसार विभिन्न संख्या में बिट्स के लिए घुमाया जाता है, डेटा की जटिलता बढ़ाता है।
• π (Pi) कदम: स्टेट ऐरे में बिट्स को पुनः व्यवस्थित करता है, बिट्स की स्थिति को बदलकर पंक्तियों और कॉलमों में डिफ्यूजन प्राप्त करता है।
• χ (Chi) कदम: एक गैर-रेखीय चरण जो प्रत्येक पंक्ति के प्रत्येक बिट पर XOR ऑपरेशन करता है, इसमें स्वयं, इसके तत्काल पड़ोसी, और पड़ोसी के पूरक को शामिल किया जाता है। यह एक स्थानीय ऑपरेशन है जो क्रिप्टोग्राफिक एल्गोरिदम की गैर-रेखीय विशेषताओं को बढ़ाता है।
• ι (Iota) कदम: एक राउंड कॉन्स्टेंट को स्टेट ऐरे के एक भाग में पेश करता है, जिसमें प्रत्येक राउंड में कॉन्स्टेंट अलग होता है, यह सुनिश्चित करने के लिए कि सभी राउंड्स समान रूप से कार्य न करें, अप्रत्याशितता को पेश करता है।

Keccak-f इन कदमों के माध्यम से उच्च स्तरीय सुरक्षा प्रदान करता है। इसका डिज़ाइन सुनिश्चित करता है कि इनपुट में मामूली परिवर्तन से स्टेट ऐरे में व्यापक और अप्रत्याशित परिवर्तन होते हैं, जो भ्रम (जिससे हमलावरों के लिए आउटपुट से इनपुट का अनुमान लगाना मुश्किल होता है) और डिफ्यूजन (जहाँ इनपुट में मामूली परिवर्तन से आउटपुट के कई हिस्सों पर प्रभाव पड़ता है) के सिद्धांतों के माध्यम से प्राप्त किया जाता है।

Keccak-f के डिज़ाइन में विभिन्न सुरक्षा स्तरों और अनुप्रयोग परिदृश्यों में पैरामीटर्स (जैसे कि स्टेट आकार और राउंड्स की संख्या) के समायोजन की अनुमति होती है, जो महान लचीलापन प्रदान करती है। Keccak-f[1600] अपने कुशल कार्यान्वयन के लिए प्रसिद्ध है, जो हार्डवेयर और सॉफ्टवेयर दोनों में उच्च प्रोसेसिंग गति प्राप्त करता है, विशेष रूप से जब बड़ी मात्रा में डेटा को संभालते समय।

निचोड़ने का चरण:

एक बार जब सभी इनपुट डेटा ब्लॉक आंतरिक स्थिति में अवशोषित हो जाते हैं, तो स्पंज संरचना निचोड़ने के चरण में प्रवेश करती है। इस चरण में, आंतरिक स्थिति के हिस्सों को क्रमिक रूप से हैश फ़ंक्शन के परिणाम के रूप में आउटपुट किया जाता है। यदि आवश्यक आउटपुट लंबाई एक बार में निचोड़े जा सकने वाली मात्रा से अधिक होती है, तो स्पंज संरचना पुनः परिवर्तन फंक्शन को लागू करती है ताकि आंतरिक स्थिति को फिर से बदल सके, फिर अधिक डेटा को आउटपुट करना जारी रखती है। यह प्रक्रिया वांछित आउटपुट लंबाई तक पहुँचने तक जारी रखी जाती है।

SHA-3 के डिजाइन का लक्ष्य SHA-2 की तुलना में उच्च सुरक्षा प्रदान करना और क्वांटम कंप्यूटिंग हमलों के खिलाफ बेहतर प्रतिरोध प्रदान करना है। इसकी अनूठी स्पंज संरचना के कारण, SHA-3 सैद्धांतिक रूप से वर्तमान में ज्ञात सभी क्रिप्टोग्राफिक हमला विधियों, जिसमें संघर्ष हमले, प्रीइमेज हमले, और दूसरे प्रीइमेज हमले शामिल हैं, का प्रतिरोध करने में सक्षम है।

RIPEMD-160 (RACE इंटीग्रिटी प्रिमिटिव्स इवैल्यूएशन मैसेज डाइजेस्ट)

RIPEMD-160 एक क्रिप्टोग्राफिक हैश फ़ंक्शन है जिसे सुरक्षित हैशिंग एल्गोरिथम प्रदान करने के लिए डिज़ाइन किया गया है। इसे 1996 में हांस डॉबर्टिन और अन्य लोगों द्वारा विकसित किया गया था, और यह RIPEMD (RACE इंटीग्रिटी प्रिमिटिव्स इवैल्यूएशन मैसेज डाइजेस्ट) परिवार का एक सदस्य है।

RIPEMD-160 एक 160-बिट (20-बाइट) हैश मूल्य उत्पन्न करता है, जो इसके नाम में "160" की उत्पत्ति है। यह MD4 के डिजाइन पर आधारित है और MD5 और SHA-1 जैसे अन्य हैशिंग एल्गोरिदम्स से प्रभावित है। RIPEMD-160 में दो समानांतर, समान क्रियाएँ शामिल हैं जो इनपुट डेटा को अलग-अलग प्रोसेस करती हैं और फिर इन दो प्रक्रियाओं के परिणामों को संयोजित करके अंतिम हैश मूल्य उत्पन्न करती हैं। इस डिज़ाइन का उद्देश्य सुरक्षा को बढ़ाना है।

RIPEMD-160 की गणना प्रक्रिया में कई मूलभूत चरण शामिल हैं: पैडिंग, ब्लॉक प्रोसेसिंग, और संपीड़न:

• पैडिंग: इनपुट संदेश को पहले पैड किया जाता है ताकि इसकी लंबाई मॉड्यूलो 512 बिट्स 448 बिट्स के बराबर हो। पैडिंग हमेशा एक बिट के 1 के साथ शुरू होती है जिसके बाद 0 बिट्स की एक शृंखला होती है, अंत में मूल संदेश की लंबाई का 64-बिट प्रतिनिधित्व होता है।
• ब्लॉक प्रोसेसिंग: पैड किया गया संदेश 512-बिट ब्लॉक्स में विभाजित किया जाता है।
• आरंभीकरण: इसमें पांच 32-बिट रजिस्टर्स (A, B, C, D, E) का उपयोग होता है, जो कुछ विशिष्ट मानों पर आरंभीकृत होते हैं।
• संपीड़न फ़ंक्शन: प्रत्येक ब्लॉक को बारी-बारी से संसाधित किया जाता है, इन पांच रजिस्टर्स के मूल्यों को एक शृंखला के जटिल ऑपरेशनों के माध्यम से अपडेट करता है। इस प्रक्रिया में बिटवाइज़ ऑपरेशन्स (जैसे जोड़, AND, OR, NOT, सर्कुलर लेफ्ट शिफ्ट्स) और एक सेट ऑफ फिक्स्ड कॉन्स्टेंट्स का उपयोग शामिल है।
• आउटपुट: सभी ब्लॉक्स को संसाधित करने के बाद, इन पांच रजिस्टर्स के मूल्यों को जोड़कर अंतिम 160-बिट हैश मूल्य बनाया जाता है।