Qu'est-ce qu'une Valeur de Hachage ?

Une valeur de hachage est une chaîne ou un nombre de taille fixe généré à partir de toute taille de données d'entrée par une fonction de hachage. Ces fonctions acceptent des entrées diverses comme du texte, des images et des vidéos, produisant une valeur de hachage irréversible de longueur fixe. Les valeurs de hachage sont déterministes, ce qui signifie que des entrées identiques produisent toujours le même résultat. Elles présentent également une résistance aux collisions, rendant difficile la recherche d'entrées distinctes qui produisent le même résultat.

Fonctions de la Valeur de Hachage

Les valeurs de hachage jouent des rôles essentiels dans l'informatique et les TI, offrant un résumé de longueur fixe des données, quelle que soit leur taille. Ces fonctions facilitent diverses applications :

• Vérification de l'intégrité des données : Utilisée pour vérifier si les données restent inchangées lors de la transmission, garantissant l'intégrité des fichiers téléchargés.
• Stockage des mots de passe : Les mots de passe sont stockés sous forme de valeurs de hachage pour la sécurité, rendant difficile la récupération des mots de passe originaux à partir des bases de données compromises.
• Récupération rapide des données : Les valeurs de hachage agissent comme des indices dans les tables de hachage, permettant des opérations de données efficaces.
• Déduplication des données : Aide à identifier et à supprimer les éléments de données en double en comparant les valeurs de hachage.
• Signature numérique et vérification : Assure l'intégrité des données et leur origine grâce à la cryptographie à clé publique et aux fonctions de hachage.
• Technologie Blockchain : Utilise les valeurs de hachage pour sécuriser les enregistrements de transactions et garantir l'immuabilité des données.
• Horodatage infalsifiable : Fournit un horodatage irréversible pour les données, utile dans la protection légale et des droits d'auteur.

Les valeurs de hachage sont efficaces dans ces domaines en raison de leurs caractéristiques clés : rapidité, déterminisme, irréversibilité et résistance aux collisions. Bien utilisées, les fonctions de hachage peuvent fournir un soutien robuste dans la sécurisation des données, l'amélioration de l'efficacité et la vérification de l'authenticité des informations.

Qu'est-ce qu'une fonction de hachage ?

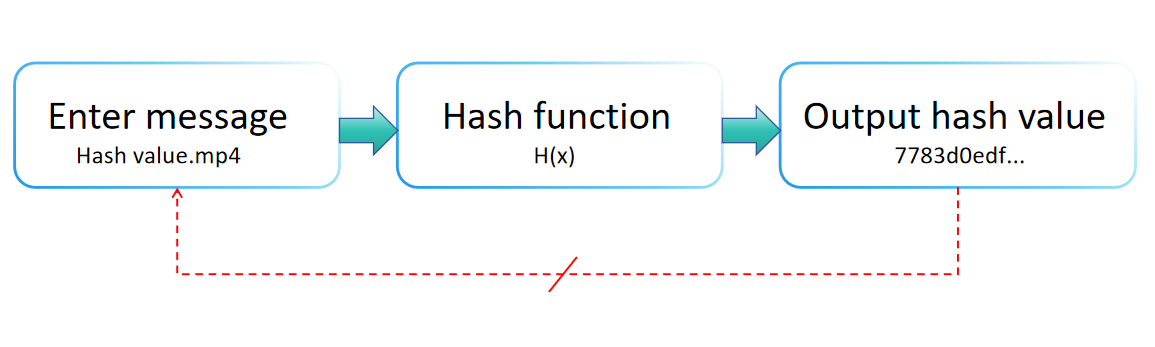
Une fonction de hachage est une construction mathématique qui associe des données d'entrée (ou "message") à une chaîne de taille fixe, généralement une valeur numérique, comme illustré dans le diagramme ci-dessous. Largement utilisée dans la gestion des données et la sécurité de l'information, une fonction de hachage se caractérise par sa performance de calcul efficace, sa longueur de sortie constante, son irréversibilité, sa sensibilité aux variations d'entrée et sa résistance aux collisions.

Performance de calcul efficace

Les fonctions de hachage peuvent rapidement calculer des valeurs de hachage à partir de données de toute forme, quelle que soit la taille des données. Cette caractéristique est cruciale pour les applications nécessitant un accès rapide aux données, telles que les tables de hachage. Cela est dû au fait que, lors du stockage des données dans des tables de hachage, la vitesse de la fonction de hachage détermine la vitesse de récupération des données. Les tables de hachage utilisent des fonctions de hachage pour localiser rapidement l'emplacement de stockage des données, en s'appuyant sur la capacité de calcul rapide des fonctions de hachage.

De plus, dans les systèmes devant traiter de grandes quantités de données, l'efficacité des fonctions de hachage impacte directement la performance globale du système. Si une fonction de hachage est lente, elle deviendra un goulot d'étranglement dans la performance du système. Certains systèmes en temps réel, comme le filtrage de paquets dans les dispositifs réseau, nécessitent un calcul immédiat des valeurs de hachage pour les données afin de prendre rapidement des décisions. Dans ces cas, l'efficacité des fonctions de hachage est tout aussi cruciale.

Par exemple, considérez une plateforme de commerce en ligne où les utilisateurs peuvent entrer des noms de produits dans la barre de recherche pour trouver des produits. Le système backend peut utiliser des fonctions de hachage pour localiser rapidement les informations sur les produits stockées dans des tables de hachage. Si le processus de calcul de la fonction de hachage est lent, l'expérience utilisateur sera gravement affectée, car ils devront attendre plus longtemps pour obtenir les résultats de la recherche. Dans cette situation, la performance de calcul efficace des fonctions de hachage assure des temps de réponse rapides, améliorant ainsi l'expérience utilisateur. [En savoir plus]

Consistance de la longueur de sortie dans les fonctions de hachage

Les fonctions de hachage transforment une entrée de n'importe quelle longueur en une sortie de longueur fixe à travers une série complexe de calculs. Ce processus implique souvent de diviser les données d'entrée en blocs de taille fixe (pour les entrées dépassant la taille de l'unité de traitement), d'appliquer une série d'opérations mathématiques et logiques à chaque bloc, puis de combiner ou d'accumuler les résultats de ces opérations d'une certaine manière pour produire finalement une valeur de hachage de taille fixe.

Pourquoi est-ce important ? La consistance de la longueur de sortie aide à assurer la sécurité des fonctions de hachage. Si la longueur de la sortie du hachage pouvait varier, cela pourrait divulguer des informations sur la taille des données originales, ce qui pourrait potentiellement être exploité pour attaquer le système dans certains scénarios. De plus, une longueur de sortie fixe rend également difficile pour les attaquants de déduire les caractéristiques des données d'entrée en analysant la longueur de sortie. En même temps, les sorties de longueur fixe simplifient le stockage et la comparaison des valeurs de hachage. Les concepteurs de systèmes peuvent savoir à l'avance combien d'espace chaque valeur de hachage occupera, ce qui est très important pour des scénarios tels que la conception de bases de données et la transmission réseau. En outre, la consistance de la longueur de sortie devient très efficace pour comparer si les valeurs de hachage sont égales car cela nécessite uniquement de comparer des données de longueur fixe. Cela est particulièrement important lors de l'utilisation de tables de hachage pour une récupération rapide des données.

Prenant SHA-256 comme exemple, cette fonction de hachage cryptographique largement utilisée produit toujours une valeur de hachage de 256 bits (c'est-à-dire 32 octets), que les données d'entrée soient un seul octet ou plusieurs millions d'octets. Cette consistance garantit que les valeurs de hachage SHA-256 peuvent être utilisées pour diverses applications de sécurité, telles que les signatures numériques et les codes d'authentification de message (MAC), tout en simplifiant le flux de travail de traitement et de stockage des données.

Irreversibilité des fonctions de hachage

Les fonctions de hachage sont unidirectionnelles, signifiant qu'il est impossible de déduire les données originales à partir de la valeur de hachage. Cette caractéristique est particulièrement importante pour le stockage des mots de passe, car même si la base de données est compromise, les attaquants ne peuvent pas récupérer les mots de passe à partir des valeurs de hachage. L'irréversibilité des fonctions de hachage repose principalement sur les principes et caractéristiques suivants :

• Compression : Les fonctions de hachage peuvent mapper des entrées de toute longueur (qui peuvent être très grandes en pratique) vers une sortie de longueur fixe. Cela signifie qu'il y a infiniment beaucoup d'entrées possibles mappées vers un nombre fini de sorties. Comme l'espace de sortie (valeurs de hachage) est beaucoup plus petit que l'espace d'entrée, différentes entrées produiront inévitablement la même sortie, un phénomène connu sous le nom de "collision". En raison de cette compression, il est impossible de déterminer l'entrée spécifique à partir d'une sortie donnée (valeur de hachage).
• Haute non-linéarité et complexité : Les fonctions de hachage sont conçues en utilisant des opérations mathématiques et logiques complexes (telles que les opérations bit à bit, les opérations modulo, etc.), pour garantir que la sortie est très sensible à l'entrée. Même de petits changements dans l'entrée (par exemple, changer un bit) peuvent provoquer des changements importants et imprévisibles dans la sortie (valeur de hachage). Ce haut degré de non-linéarité et le caractère aléatoire de la sortie rendent extrêmement difficile de déduire l'entrée originale à partir de la valeur de hachage.
• Unidirectionnalité : La conception des fonctions de hachage garantit que leur fonctionnement est à sens unique ; c'est-à-dire que si le calcul de la valeur de hachage est facile, le processus inverse (récupérer les données originales à partir de la valeur de hachage) n'est pas faisable. Cela est dû au fait que le processus de calcul des fonctions de hachage implique une série d'opérations irréversibles (telles que l'irréversibilité des opérations modulo), garantissant que même avec la valeur de hachage, il est impossible de rétro-concevoir les données originales.
• Cartographie aléatoire : Une fonction de hachage idéale devrait agir comme un "cartographe aléatoire", signifiant que chaque entrée possible est également susceptible d'être mappée à n'importe quel point dans l'espace de sortie. Cette propriété garantit qu'il n'y a aucun moyen faisable de prédire à quel résultat une entrée spécifique sera mappée, renforçant l'irréversibilité de la fonction de hachage.
• Fondation mathématique : Mathématiquement, l'irréversibilité des fonctions de hachage peut être comprise grâce à leur dépendance à des "problèmes de logarithme discret", "problèmes de factorisation de grands entiers" ou d'autres problèmes de théorie des nombres qui sont difficiles à résoudre avec les capacités mathématiques et informatiques actuelles. Par exemple, la conception de certains algorithmes de hachage peut dépendre indirectement de la difficulté de calcul de ces problèmes, garantissant ainsi leur irréversibilité.

Sensibilité aux entrées et l'effet avalanche

Dans la conception des fonctions de hachage, des opérations mathématiques et logiques complexes (telles que les opérations bit à bit, les opérations modulo, etc.) sont utilisées pour garantir que la sortie soit hautement sensible à l'entrée. Même de petits changements dans l'entrée (par exemple, changer un seul bit) entraîneront des changements significatifs et imprévisibles dans la sortie (la valeur de hachage), un phénomène connu sous le nom d'« effet avalanche ». [En savoir plus]

Résistance aux collisions en cryptographie

La résistance aux collisions d'une fonction de hachage est un concept crucial en cryptographie, indiquant le niveau de sécurité d'une fonction de hachage contre les attaques par collisions. Cette propriété implique que pour toute fonction de hachage H, il est pratiquement infaisable de trouver deux entrées distinctes x et y (x ≠ y) telles que H(x) = H(y). Une fonction de hachage avec une solide résistance aux collisions rend extrêmement difficile de trouver deux entrées différentes menant à la même valeur de sortie.

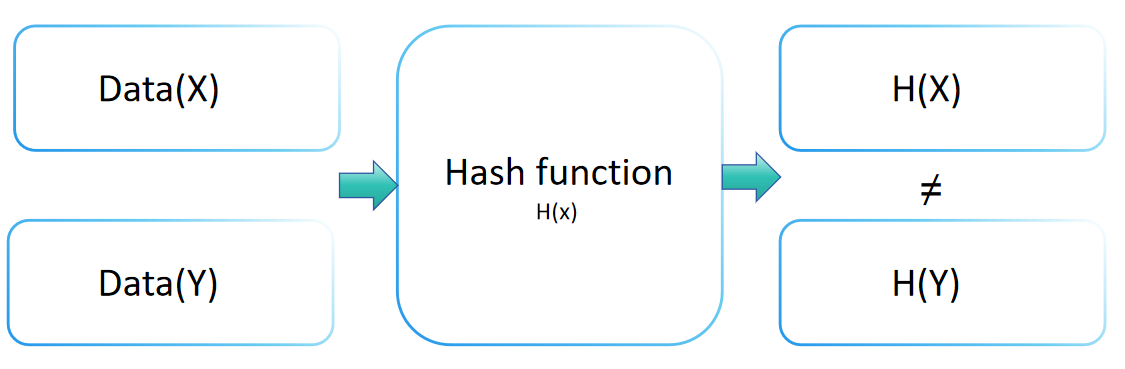
La résistance aux collisions joue un rôle vital dans le maintien de l'intégrité des données et la vérification. En transformant les informations d'entrée en une sortie de taille fixe (ou empreinte), les fonctions de hachage garantissent qu'aucune deux entrées différentes ne produisent la même sortie. Cette caractéristique unique permet à la valeur de hachage d'identifier précisément la valeur originale.

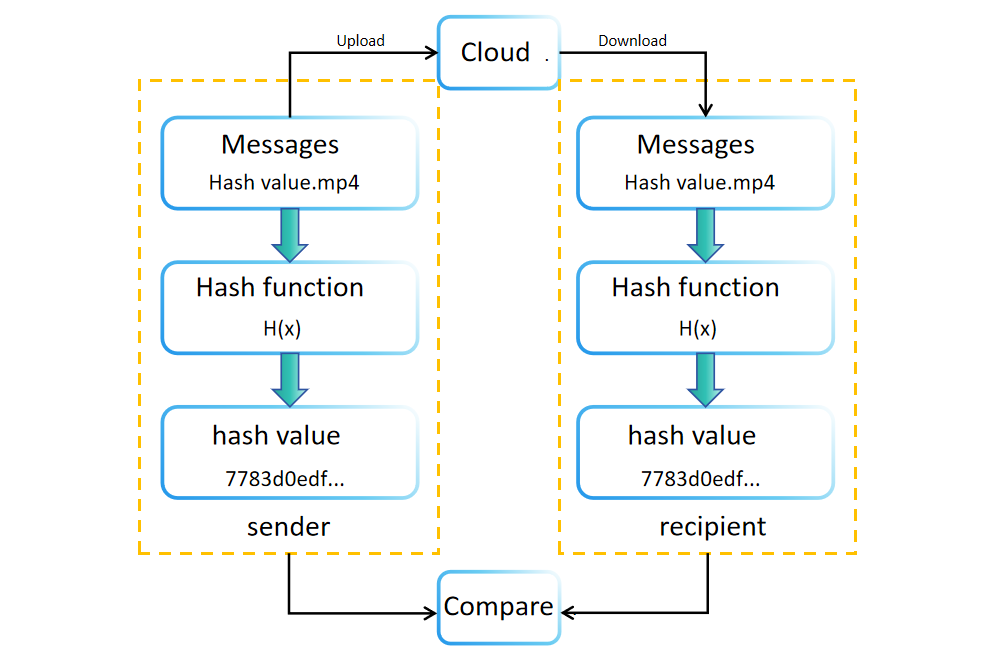
Lors de la création ou du stockage de données, une valeur de hachage (ou empreinte) est générée en utilisant une fonction de hachage. Cette valeur est stockée ou transmise aux côtés des données originales. Par exemple, les sites de téléchargement de logiciels affichent souvent les valeurs de hachage des fichiers pour la vérification de l'intégrité. Les destinataires peuvent recalculer indépendamment la valeur de hachage des données reçues pour confirmer leur intégrité. Si les valeurs de hachage originales et recalculées correspondent, l'intégrité des données est vérifiée. Sinon, les données peuvent avoir été altérées ou corrompues pendant la transmission ou le stockage.

Comparer les valeurs de hachage offre également l'avantage de vérifier l'intégrité des données sans nécessiter un espace de stockage important. Cette méthode permet aux destinataires de confirmer l'authenticité des données en comparant simplement les valeurs de hachage avant et après la transmission.

Les collisions de hachage peuvent-elles être trouvées ?

À travers les caractéristiques des fonctions de hachage mentionnées ci-dessus, nous avons compris la résistance aux collisions. Mais est-il possible que des collisions de hachage existent, c'est-à-dire que deux entrées différentes produisent le même résultat ? La réponse est affirmative, les collisions existent bien. Selon le principe des tiroirs, tant que l'espace d'entrée est suffisamment grand, il existe une possibilité de collisions de hachage. Cela est dû au fait que l'espace de sortie des fonctions de hachage est généralement beaucoup plus petit que l'espace d'entrée, conduisant inévitablement à plusieurs entrées différentes mappées sur le même résultat.

Le principe des tiroirs est un principe simple et intuitif de mathématiques combinatoires, stipulant que si plus de n objets sont placés dans n conteneurs, alors au moins un conteneur contiendra deux objets ou plus. Ce principe peut également être utilisé pour expliquer des problèmes tels que le paradoxe des anniversaires.

L'application du principe des tiroirs est très large, avec des utilisations importantes dans des domaines tels que la cryptographie, l'informatique et les mathématiques. Par exemple, en informatique, le principe des tiroirs est utilisé pour prouver la correction de certains algorithmes ou pour analyser la complexité temporelle des algorithmes. En cryptographie, le principe des tiroirs est également utilisé pour concevoir certaines méthodes d'attaque cryptographique, comme l'attaque par anniversaires.

Le paradoxe des anniversaires est une application classique du principe des tiroirs. Supposons qu'il y ait n personnes dans une pièce. Si nous voulons que la probabilité qu'au moins deux personnes partagent le même anniversaire soit supérieure à 50 %, combien de personnes sont nécessaires ? Selon le principe des tiroirs, si 367 personnes (en supposant qu'il y ait 366 jours dans une année, plus un jour supplémentaire pour le 29 février d'une année bissextile) sont placées dans 366 « tiroirs » (c'est-à-dire les anniversaires), alors au moins un « tiroir » contiendra deux personnes, signifiant qu'au moins deux personnes partagent le même anniversaire. Ceci illustre le paradoxe des anniversaires.

Il est important de noter que, bien que le principe des tiroirs soit simple et intuitif, son application doit tenir compte du contexte spécifique. Par exemple, lors de l'application du principe des tiroirs, il est nécessaire de s'assurer que les variables aléatoires impliquées sont indépendantes les unes des autres ; sinon, cela peut conduire à des conclusions incorrectes. De plus, dans certains cas, il est également nécessaire de prendre en compte des facteurs tels que la taille et la forme des tiroirs.

Cependant, tenter de trouver des collisions de hachage en parcourant simplement l'espace d'entrée peut ne pas être pratique, principalement pour deux raisons :

• Complexité computationnelle : Pour la plupart des fonctions de hachage, l'espace d'entrée est vaste. Prenons SHA-256 comme exemple ; sa sortie est une valeur de hachage de 256 bits, ce qui signifie qu'il a 2^256 sorties possibles. Puisque l'un des objectifs de conception des fonctions de hachage est de minimiser autant que possible les collisions, théoriquement, trouver une collision de hachage pour SHA-256 nécessiterait de parcourir environ 2^(256/2) = 2^128 entrées, selon le paradoxe des anniversaires, qui est le nombre approximatif d'entrées attendu pour trouver une collision. Même avec les superordinateurs les plus puissants actuellement disponibles, il faudrait bien au-delà d'une vie humaine pour achever une telle tâche. Spécifiquement, le temps pour parcourir 2^128 entrées dépasse de loin l'âge de l'humanité, rendant considéré comme impossible de trouver une collision de hachage SHA-256 par simple parcours.
• Conception des fonctions de hachage : Les fonctions de hachage sont généralement conçues pour rendre la recherche de collisions computationnellement infaisable. Cela signifie que, bien que les collisions existent théoriquement, elles sont pratiquement impossibles à trouver en pratique. C'est une caractéristique importante des fonctions de hachage cryptographiques (telles que SHA-256), qui sont largement utilisées dans des domaines tels que les signatures numériques, le stockage des mots de passe, et plus encore.

Bien sûr, nous pouvons également utiliser des algorithmes spécifiques pour essayer de trouver des collisions de hachage. Ces algorithmes exploitent souvent certaines propriétés ou faiblesses connues des fonctions de hachage pour trouver des collisions. Voici quelques techniques et méthodes courantes pour trouver des collisions de hachage :

• Attaque par anniversaires : C'est une méthode simple basée sur la probabilité utilisée pour estimer le temps nécessaire pour trouver une collision lorsque les entrées sont choisies au hasard. Le principe de l'attaque par anniversaires est que s'il y a beaucoup de personnes dans une pièce, la probabilité que deux personnes aient le même anniversaire augmente avec le nombre de personnes. De manière similaire, dans les fonctions de hachage, si un nombre suffisant d'entrées sont sélectionnées au hasard, il est probable que deux entrées produiront finalement la même sortie de hachage.
• Attaque par force brute : C'est la méthode la plus simple, qui implique de parcourir toutes les entrées possibles pour trouver une collision. Cependant, cette méthode est peu pratique pour les fonctions de hachage avec de grands espaces d'entrée en raison des énormes ressources computationnelles et du temps requis.
• Tables arc-en-ciel : Cette technique est utilisée pour précalculer et stocker un grand nombre de valeurs de hachage et leurs entrées correspondantes. Les tables arc-en-ciel sont particulièrement utiles pour craquer les mots de passe qui n'ont pas utilisé d'obfuscation de données aléatoires ou qui ont une fonction de hachage connue. En consultant la table arc-en-ciel, un attaquant peut rapidement trouver une entrée qui correspond à une valeur de hachage spécifique.
• Attaques par extension de hachage : Certaines fonctions de hachage permettent aux attaquants de combiner des données supplémentaires avec une valeur de hachage connue sans connaître l'entrée d'origine, générant ainsi une nouvelle valeur de hachage. Cette attaque peut être utilisée pour construire des collisions ou effectuer d'autres types d'attaques.
• Entrées spécialement construites : Parfois, les attaquants peuvent exploiter des faiblesses spécifiques ou des comportements non linéaires dans les fonctions de hachage pour construire des entrées spéciales qui sont plus susceptibles de produire des collisions dans la fonction de hachage.

Quelles sont les fonctions de hachage couramment utilisées ?

MD5 (Message Digest Algorithm 5)

MD5 est une fonction de hachage cryptographique largement utilisée, conçue par Ronald Rivest dans les années 1990 pour remplacer l'ancien algorithme MD4. Elle peut convertir un message de n'importe quelle longueur en une valeur de hachage de longueur fixe (128 bits, soit 16 octets). L'objectif de la conception de MD5 était de fournir un moyen rapide et relativement sûr de générer une empreinte numérique des données. Cependant, des méthodes de collision pour MD5 ont été découvertes, rendant l'algorithme non sécurisé, mais il est toujours largement utilisé dans des situations où la sécurité n'est pas une préoccupation principale.

Le processus de calcul de MD5 comprend les étapes suivantes :

• Rembourrage : Initialement, les données originales sont rembourrées pour que leur longueur en octets soit un multiple de 512. Le rembourrage commence par un 1, suivi de 0 jusqu'à ce que l'exigence de longueur soit satisfaite.
• Ajout de la longueur : Une valeur de longueur de 64 bits, qui est la représentation binaire de la longueur du message original, est ajoutée au message rembourré, rendant la longueur finale du message un multiple de 512 bits.
• Initialisation du tampon MD : Quatre registres de 32 bits (A, B, C, D) sont initialisés pour stocker les valeurs de hachage intermédiaires et finales.
• Traitement des blocs de messages : Le message rembourré et traité en longueur est divisé en blocs de 512 bits, et chaque bloc est traité à travers quatre tours d'opération. Chaque tour inclut 16 opérations similaires basées sur des fonctions non linéaires (F, G, H, I), des opérations de décalage circulaire gauche et une addition modulo 32.
• Sortie : La valeur de hachage finale est le contenu du dernier état des quatre registres A, B, C, D concaténés ensemble (chaque registre est de 32 bits), formant une valeur de hachage de 128 bits.

SHA-1 (Secure Hash Algorithm 1)

SHA-1 a été conçu par la National Security Agency (NSA) des États-Unis et publié comme Federal Information Processing Standard (FIPS PUB 180-1) par le National Institute of Standards and Technology (NIST) en 1995. SHA-1 est destiné à être utilisé dans les signatures numériques et autres applications cryptographiques, générant une valeur de hachage de 160 bits (20 octets) connue sous le nom de message digest. Bien qu'il soit désormais connu que SHA-1 présente des vulnérabilités de sécurité et a été remplacé par des algorithmes plus sécurisés tels que SHA-256 et SHA-3, comprendre son principe de fonctionnement conserve une valeur éducative et historique.

Le but de la conception de SHA-1 est de prendre un message de longueur arbitraire et de produire un message digest de 160 bits pour vérifier l'intégrité des données. Son processus de calcul peut être divisé en les étapes suivantes :

• Rembourrage : Initialement, le message original est rembourré pour que sa longueur (en bits) modulo 512 soit égale à 448. Le rembourrage commence toujours par un bit "1", suivi de plusieurs bits "0", jusqu'à ce que la condition de longueur ci-dessus soit remplie.
• Ajout de la longueur : Un bloc de 64 bits est ajouté au message rembourré, représentant la longueur du message original (en bits), rendant la longueur finale du message un multiple de 512 bits.
• Initialisation du tampon : L'algorithme SHA-1 utilise un tampon de 160 bits, divisé en cinq registres de 32 bits (A, B, C, D, E), pour stocker les valeurs de hachage intermédiaires et finales. Ces registres sont initialisés à des valeurs constantes spécifiques au début de l'algorithme.
• Traitement des blocs de messages : Le message pré-traité est divisé en blocs de 512 bits. Pour chaque bloc, l'algorithme exécute une boucle principale contenant 80 étapes similaires. Ces 80 étapes sont divisées en quatre tours, chacun avec 20 étapes. Chaque étape utilise une fonction non linéaire différente (F, G, H, I) et une constante (K). Ces fonctions sont conçues pour augmenter la complexité et la sécurité des opérations. Dans ces étapes, l'algorithme utilise des opérations binaires (telles que ET, OU, XOR, NON) et une addition modulo 32, ainsi que des décalages circulaires gauche.
• Sortie : Après avoir traité tous les blocs, les valeurs accumulées dans les cinq registres sont concaténées pour former la valeur de hachage finale de 160 bits.

SHA-2 (Algorithme de Hachage Sécurisé 2)

SHA-2 est une famille de fonctions de hachage cryptographiques, comprenant plusieurs versions différentes, principalement constituées de six variantes : SHA-224, SHA-256, SHA-384, SHA-512, SHA-512/224 et SHA-512/256. SHA-2 a été conçu par la National Security Agency (NSA) des États-Unis et publié comme un Standard Fédéral de Traitement de l'Information (FIPS) par le National Institute of Standards and Technology (NIST). Comparé à son prédécesseur, SHA-1, SHA-2 offre une sécurité renforcée, principalement reflétée dans des valeurs de hachage plus longues et une résistance plus forte aux attaques par collision.

Le fonctionnement de la famille SHA-2 est similaire à SHA-1 à bien des égards mais offre une sécurité plus élevée grâce à l'utilisation de valeurs de hachage plus longues et une procédure de traitement plus complexe. Voici les principales étapes de l'algorithme SHA-2 :

• Rembourrage : Le message d'entrée est d'abord rembourré pour rendre sa longueur, moins 64 bits, égale à 448 ou 896 sur une base modulo 512 (pour SHA-224 et SHA-256) ou modulo 1024 (pour SHA-384 et SHA-512). La méthode de rembourrage est la même que SHA-1, qui consiste à ajouter un "1" à la fin du message, suivi de plusieurs "0", et finalement une représentation binaire de 64 bits (pour SHA-224 et SHA-256) ou 128 bits (pour SHA-384 et SHA-512) de la longueur du message original en bits.
• Initialisation du Tampon : L'algorithme SHA-2 utilise un ensemble de valeurs de hachage initialisées comme tampon de départ, selon la variante SHA-2 choisie. Par exemple, SHA-256 utilise huit registres de 32 bits, tandis que SHA-512 utilise huit registres de 64 bits. Ces registres sont initialisés à des valeurs constantes spécifiques.
• Traitement des Blocs de Messages : Le message rembourré est divisé en blocs de 512 bits ou 1024 bits, et chaque bloc subit plusieurs tours d'opérations cryptographiques. SHA-256 et SHA-224 effectuent 64 tours d'opérations, tandis que SHA-512, SHA-384, SHA-512/224 et SHA-512/256 effectuent 80 tours. Chaque tour d'opération comprend une série d'opérations complexes en bits, incluant des opérations logiques, d'addition modulaire et conditionnelles, en s'appuyant sur différentes fonctions non linéaires et des constantes prédéfinies. Ces opérations augmentent la complexité et la sécurité de l'algorithme.
• Sortie : Finalement, après avoir traité tous les blocs, les valeurs dans le tampon sont combinées pour former la valeur de hachage finale. Selon la variante SHA-2, cette valeur de hachage peut être de 224, 256, 384 ou 512 bits de longueur.

Vous pourriez être curieux de savoir pourquoi l'entrée d'une fonction de hachage peut être de longueur arbitraire, mais la sortie est fixe. La raison est que la famille SHA-2 utilise la transformation de Merkle-Damgård, qui permet la construction de fonctions de hachage pouvant traiter des messages de n'importe quelle longueur à partir d'une fonction de compression de longueur fixe. La transformation de Merkle-Damgård est adoptée dans de nombreuses fonctions de hachage traditionnelles, y compris MD5 et SHA-1.

L'idée centrale de la transformation de Merkle-Damgård est de diviser le message d'entrée en blocs de taille fixe, puis de traiter ces blocs un par un, chaque étape de traitement dépendant du résultat de la précédente, pour produire finalement une valeur de hachage de taille fixe. L'étape de padding de SHA-256 incarne les principes de base de la transformation de Merkle-Damgård, à savoir en appliquant un padding approprié pour traiter des messages de toute longueur et en s'assurant que la longueur finale du message traité respecte certaines conditions (comme être un multiple d'une longueur fixe). Ainsi, on peut dire que l'étape de padding de SHA-256 suit la méthode de transformation de Merkle-Damgård.

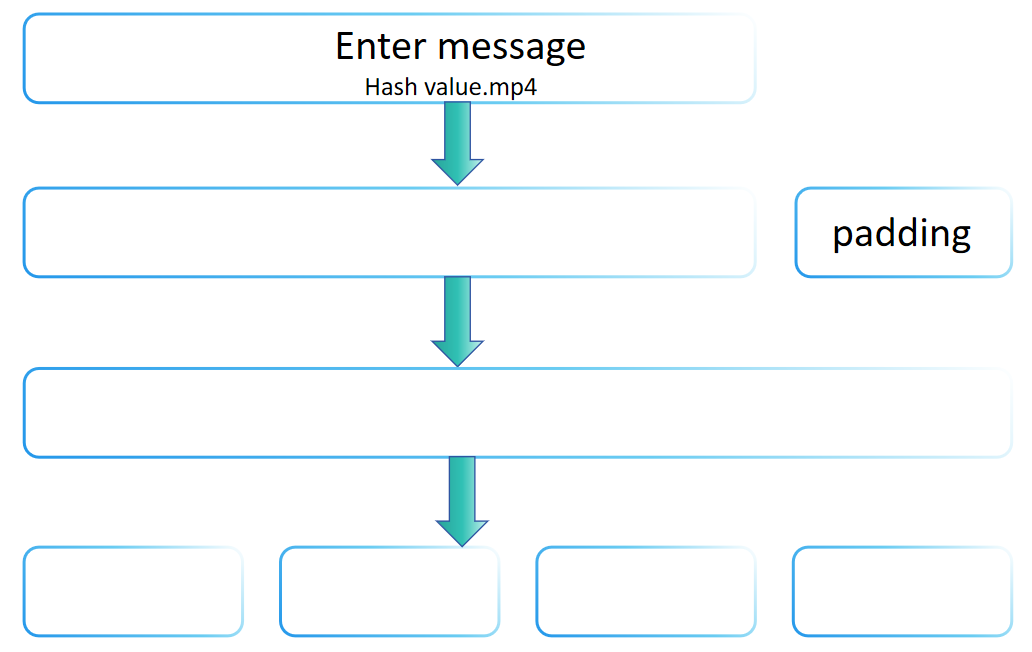
Cependant, SHA-256 n'est pas simplement une mise en œuvre directe de la transformation de Merkle-Damgård. Il comprend également une série d'étapes de calcul complexes (telles que l'expansion des messages, de multiples tours de fonctions de compression, etc.), qui sont des conceptions uniques de SHA-256, visant à renforcer sa sécurité. Par conséquent, bien que SHA-256 suive les principes de la transformation de Merkle-Damgård dans son étape de padding, il renforce la sécurité globale en introduisant d'autres mécanismes de sécurité, ce qui fait qu'il ne se limite pas uniquement au cadre de base de la transformation de Merkle-Damgård.

SHA-3 (Secure Hash Algorithm 3)

SHA-3 est le dernier standard de hachage sécurisé, officiellement approuvé par le National Institute of Standards and Technology (NIST) en 2015 comme Federal Information Processing Standard (FIPS 202). SHA-3 n'est pas destiné à remplacer les précédents SHA-1 ou SHA-2 (car SHA-2 est toujours considéré comme sûr), mais plutôt pour compléter et offrir une option alternative au sein de la famille SHA, fournissant un algorithme de hachage cryptographique différent. SHA-3 est basé sur l'algorithme Keccak, conçu par Guido Bertoni et d'autres, et a été le gagnant du concours SHA-3 organisé par le NIST en 2012.

Le principe de fonctionnement de SHA-3 diffère considérablement de celui de SHA-2, principalement parce qu'il utilise une méthode connue sous le nom de "construction éponge" pour absorber et presser les données, produisant la valeur de hachage finale. Cette méthode permet à SHA-3 de fournir de manière flexible des valeurs de hachage de différentes longueurs, offrant ainsi une gamme d'applications plus large que SHA-2. Voici les principales étapes de SHA-3 :

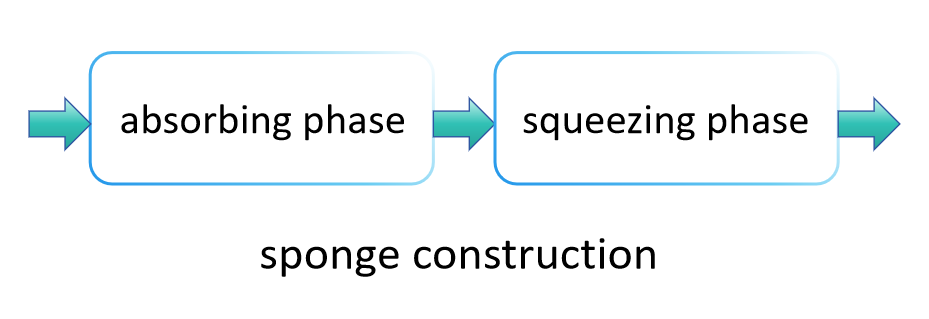
Phase d'absorption :

Dans la phase d'absorption, la structure éponge divise d'abord les données d'entrée en blocs de taille fixe. Ces blocs de données sont séquentiellement "absorbés" dans l'état interne de l'éponge, qui est généralement plus grand qu'un seul bloc de données, pour garantir qu'une grande quantité de données puisse être traitée sans débordement. Plus précisément, chaque bloc de données est fusionné avec une partie de l'état interne d'une manière ou d'une autre (comme par une opération XOR), suivi de l'application d'une fonction de permutation fixe (dans SHA-3, il s'agit de Keccak-f ) pour transformer l'ensemble de l'état, empêchant ainsi l'interférence entre différents blocs de données d'entrée. Ce processus est répété jusqu'à ce que tous les blocs de données d'entrée aient été traités.

Keccak-f est la fonction de permutation principale utilisée dans l'algorithme de hachage cryptographique SHA-3. Il est un composant central de la famille d'algorithmes Keccak. SHA-3 est basé sur l'algorithme Keccak, qui a remporté le concours d'algorithmes de hachage cryptographique organisé par le NIST et a été sélectionné comme standard pour SHA-3. La fonction Keccak-f a plusieurs variantes, la plus couramment utilisée étant Keccak-f[1600], où le nombre indique la largeur de bit sur laquelle elle opère.

Keccak-f est composé de plusieurs tours de la même opération (appelés rondes). Pour Keccak-f[1600], il y a un total de 24 tours d'opérations. Chaque tour comprend cinq étapes de base : θ (Theta), ρ (Rho), π (Pi), χ (Chi) et ι (Iota). Ces étapes agissent ensemble sur le tableau d'état, transformant progressivement son contenu, augmentant la confusion et la diffusion pour renforcer la sécurité. Voici une brève description de ces étapes :

• Étape θ (Theta) : Effectue des opérations XOR sur tous les bits de chaque colonne, puis XOR le résultat sur les colonnes adjacentes, fournissant une diffusion entre les colonnes.
• Étape ρ (Rho) : Opération de rotation au niveau des bits, où chaque bit est tourné d'un nombre différent de bits selon des règles prédéterminées, augmentant la complexité des données.
• Étape π (Pi) : Réorganise les bits dans le tableau d'état, changeant la position des bits pour atteindre une diffusion à travers les rangées et les colonnes.
• Étape χ (Chi) : Une étape non linéaire qui effectue des opérations XOR sur chaque bit de chaque rangée, y compris elle-même, son voisin immédiat et le complément du voisin. C'est une opération locale qui augmente les caractéristiques non linéaires de l'algorithme cryptographique.
• Étape ι (Iota) : Introduit une constante de tour dans une partie du tableau d'état, avec la constante différant à chaque tour, pour éviter que tous les tours ne fonctionnent de manière identique, introduisant de l'imprévisibilité.

Keccak-f offre un haut niveau de sécurité grâce à ces étapes. Sa conception garantit que même de légers changements dans l'entrée entraînent des changements généralisés et imprévisibles dans le tableau d'état, réalisés grâce aux principes de confusion (rendant difficile pour les attaquants de déduire l'entrée à partir de la sortie) et de diffusion (où de légers changements dans l'entrée affectent plusieurs parties de la sortie).

La conception de Keccak-f permet d'ajuster les paramètres (comme la taille de l'état et le nombre de tours) à différents niveaux de sécurité et scénarios d'application, offrant une grande flexibilité. Keccak-f[1600] est réputé pour son implémentation efficace, atteignant des vitesses de traitement élevées à la fois en matériel et en logiciel, en particulier lors du traitement de grandes quantités de données.

Phase de pressage :

Une fois que tous les blocs de données d'entrée ont été absorbés dans l'état interne, la structure éponge entre dans la phase de pressage. À ce stade, des parties de l'état interne sont progressivement sorties comme le résultat de la fonction de hachage. Si la longueur de sortie requise dépasse la quantité qui peut être extraite à la fois, la structure éponge applique la fonction de permutation pour transformer à nouveau l'état interne, puis continue à sortir plus de données. Ce processus est poursuivi jusqu'à ce que la longueur de sortie souhaitée soit atteinte.

L'objectif de la conception de SHA-3 est de fournir une sécurité supérieure à celle de SHA-2 et une meilleure résistance contre les attaques informatiques quantiques. Grâce à sa structure éponge unique, SHA-3 est théoriquement capable de résister à toutes les méthodes d'attaque cryptographiques actuellement connues, y compris les attaques par collision, les attaques par préimage et les attaques par seconde préimage.

RIPEMD-160 (RACE Integrity Primitives Evaluation Message Digest)

RIPEMD-160 est une fonction de hachage cryptographique conçue pour fournir un algorithme de hachage sécurisé. Elle a été développée en 1996 par Hans Dobbertin et d'autres, et elle fait partie de la famille RIPEMD (RACE Integrity Primitives Evaluation Message Digest).

RIPEMD-160 produit une valeur de hachage de 160 bits (20 octets), ce qui est à l'origine du "160" dans son nom. Il est basé sur la conception du MD4 et influencé par d'autres algorithmes de hachage tels que MD5 et SHA-1. RIPEMD-160 comprend deux opérations parallèles, similaires qui traitent les données d'entrée séparément puis combinent les résultats de ces deux processus pour générer la valeur de hachage finale. Cette conception vise à renforcer la sécurité.

Le processus de calcul de RIPEMD-160 inclut plusieurs étapes de base : le bourrage, le traitement des blocs et la compression :

• Bourrage : Le message d'entrée est d'abord complété pour que sa longueur modulo 512 bits soit égale à 448 bits. Le bourrage commence toujours par un seul bit de 1 suivi d'une série de bits de 0, se terminant par une représentation sur 64 bits de la longueur du message original.
• Traitement des blocs : Le message complété est divisé en blocs de 512 bits.
• Initialisation : Il utilise cinq registres de 32 bits (A, B, C, D, E), qui sont initialisés à certaines valeurs spécifiques.
• Fonction de compression : Chaque bloc est traité à son tour, mettant à jour les valeurs de ces cinq registres par une série d'opérations complexes. Ce processus comprend des opérations binaires (telles que l'addition, ET, OU, NON, rotations circulaires à gauche) et l'utilisation d'un ensemble de constantes fixes.
• Sortie : Après que tous les blocs ont été traités, les valeurs de ces cinq registres sont concaténées pour former la valeur de hachage finale de 160 bits.