Что такое хеш-значение?

Хеш-значение - это строка или число фиксированного размера, созданное из данных любого размера с помощью хеш-функции. Эти функции принимают разнообразные данные, такие как текст, изображения и видео, и производят хеш-значение фиксированной длины, которое нельзя обратно преобразовать. Хеш-значения детерминированны, что означает, что идентичные входные данные всегда приводят к одному и тому же результату. Они также обладают устойчивостью к коллизиям, что делает сложным нахождение различных входных данных, приводящих к одному и тому же результату.

Функции хеш-значения

Хеш-значения играют важную роль в компьютерных науках и информационных технологиях, предоставляя фиксированный суммарный размер данных независимо от их размера. Эти функции облегчают различные приложения:

• Проверка целостности данных: Используется для проверки, остаются ли данные неизменными во время передачи, обеспечивая целостность загруженных файлов.
• Хранение паролей: Пароли хранятся в виде хеш-значений для обеспечения безопасности, что делает восстановление исходных паролей из компрометированных баз данных трудным.
• Быстрый доступ к данным: Хеш-значения действуют как индексы в хеш-таблицах, обеспечивая эффективные операции с данными.
• Дедупликация данных: Помогает в определении и удалении дублирующихся элементов данных путем сравнения их хеш-значений.
• Цифровая подпись и верификация: Обеспечивает целостность и подлинность данных с помощью криптографии с открытым ключом и хеш-функций.
• Технология блокчейна: Использует хеш-значения для обеспечения безопасности записей транзакций и обеспечения неизменности данных.
• Неизменяемые временные метки: Предоставляет необратимую временную метку для данных, полезную для юридической и авторской защиты.

Причиной эффективности хеш-значений в этих областях являются их ключевые характеристики - скорость, детерминизм, необратимость и устойчивость к коллизиям. Правильно использованные хеш-функции могут обеспечить надежную поддержку при обеспечении безопасности данных, повышении эффективности и проверке подлинности информации.

Что такое хеш-функция?

Хеш-функция - это математическая конструкция, которая отображает входные данные (или "сообщение") на строку фиксированного размера, обычно числовое значение, как показано на диаграмме ниже. Широко используется в управлении данными и информационной безопасности, хеш-функция характеризуется своей эффективной вычислительной производительностью, постоянной длиной вывода, необратимостью, чувствительностью к вариациям ввода и устойчивостью к коллизиям.

Эффективная вычислительная производительность

Хеш-функции могут быстро вычислять хеш-значения из данных любой формы, независимо от их размера. Эта характеристика критически важна для приложений, которые требуют быстрого доступа к данным, таких как хеш-таблицы. Это связано с тем, что при сохранении данных в хеш-таблицах скорость хеш-функции определяет скорость доступа к данным. Хеш-таблицы используют хеш-функции для быстрого определения места хранения данных, полагаясь на быструю вычислительную способность хеш-функций.

Более того, в системах, которым необходимо обрабатывать большие объемы данных, эффективность хеш-функций напрямую влияет на общую производительность системы. Если хеш-функция работает медленно, она станет узким местом в производительности системы. Некоторые системы реального времени, такие как фильтрация пакетов в сетевых устройствах, требуют немедленного вычисления хеш-значений для данных, чтобы быстро принимать решения. В этих случаях эффективность хеш-функций также является крайне важной.

Например, представьте онлайн-платформу электронной коммерции, где пользователи могут вводить названия товаров в строку поиска для поиска продуктов. Бэкенд-система может использовать хеш-функции для быстрого поиска информации о продуктах, сохраненной в хеш-таблицах. Если процесс вычисления хеш-функции медленный, пользовательский опыт будет серьезно нарушен, так как им придется дольше ждать результатов поиска. В этой ситуации эффективная вычислительная производительность хеш-функций обеспечивает быстрое время отклика, тем самым улучшая пользовательский опыт. [Узнать больше]

Постоянная длина вывода в хеш-функциях

Хеш-функции преобразуют входные данные любой длины в вывод фиксированной длины с помощью сложной серии вычислений. Этот процесс часто включает в себя разделение входных данных на блоки фиксированного размера (для вводов, превышающих размер обрабатываемого блока), применение серии математических и логических операций к каждому блоку, а затем объединение или накопление результатов этих операций каким-либо образом, чтобы в конечном итоге получить хеш-значение фиксированного размера.

Почему это важно? Постоянная длина вывода помогает обеспечить безопасность хеш-функций. Если длина вывода хеша может изменяться, это может утечь информацию о размере исходных данных, что в некоторых случаях может быть использовано для атаки на систему. Более того, фиксированная длина вывода также делает сложным для злоумышленников вывод характеристик входных данных путем анализа длины вывода. В то же время фиксированная длина вывода упрощает хранение и сравнение хеш-значений. Проектировщики систем могут заранее знать, сколько места займет каждое хеш-значение, что очень важно для сценариев, таких как проектирование баз данных и передача по сети. Более того, постоянная длина вывода становится очень эффективной для сравнения хеш-значений на равенство, поскольку для этого требуется только сравнение данных фиксированной длины. Это особенно важно при использовании хеш-таблиц для быстрого доступа к данным.

Возьмем SHA-256 в качестве примера, эта широко используемая криптографическая хеш-функция всегда выдает хеш-значение длиной 256 бит (т.е. 32 байта), независимо от того, являются ли входные данные одним байтом или несколькими миллионами байт. Эта постоянство гарантирует, что хеш-значения SHA-256 могут использоваться для различных приложений безопасности, таких как цифровые подписи и коды аутентификации сообщений (MAC), упрощая при этом рабочий процесс обработки и хранения данных.

Необратимость хеш-функций

Хеш-функции являются однонаправленными, что означает, что невозможно вывести исходные данные из хеш-значения. Эта характеристика особенно важна при хранении паролей, так как даже если база данных скомпрометирована, злоумышленники не смогут восстановить пароли из хеш-значений. Необратимость хеш-функций в основном основана на следующих принципах и характеристиках:

• Сжатие: Хеш-функции могут отображать входы любой длины (которые могут быть очень большими в практическом использовании) в вывод фиксированной длины. Это означает, что существует бесконечно много возможных входов, отображаемых на конечное количество выводов. Поскольку пространство вывода (хеш-значения) намного меньше пространства ввода, разные входы неизбежно будут производить одинаковый вывод, явление, известное как "коллизия". Из-за этого сжатия невозможно определить конкретный вход из заданного вывода (хеш-значения).
• Высокая нелинейность и сложность: Хеш-функции разрабатываются с использованием сложных математических и логических операций (таких как битовые операции, операции по модулю и т. д.), чтобы обеспечить высокую чувствительность вывода к вводу. Даже незначительные изменения во входных данных (например, изменение одного бита) могут вызвать значительные и непредсказуемые изменения в выводе (хеш-значении). Этот высокий уровень нелинейности и случайности вывода делает крайне сложным вывод исходных данных из хеш-значения.
• Однонаправленность: Конструкция хеш-функций обеспечивает однонаправленность их работы; то есть, хотя вычисление хеш-значения легко, обратный процесс (восстановление исходных данных из хеш-значения) невозможен. Это потому, что процесс вычисления хеш-значения включает в себя серию необратимых операций (например, необратимость операций по модулю), обеспечивая тем самым невозможность обратной инженерии исходных данных даже с хеш-значением.
• Случайное отображение: Идеальная хеш-функция должна действовать как "случайное отображение", что означает, что каждый возможный вход одинаково вероятно будет отображен в любую точку в пространстве вывода. Это свойство обеспечивает отсутствие практического способа предсказать, к какому выводу конкретный ввод будет отображен, что усиливает необратимость хеш-функции.
• Математическое основание: Математически необратимость хеш-функций можно понять через их зависимость от "задачи дискретного логарифма", "задач разложения больших целых чисел" или других задач теории чисел, решение которых сложно с текущими математическими и вычислительными возможностями. Например, конструкция некоторых хеш-алгоритмов может косвенно зависеть от вычислительной сложности этих задач, тем самым обеспечивая их необратимость.

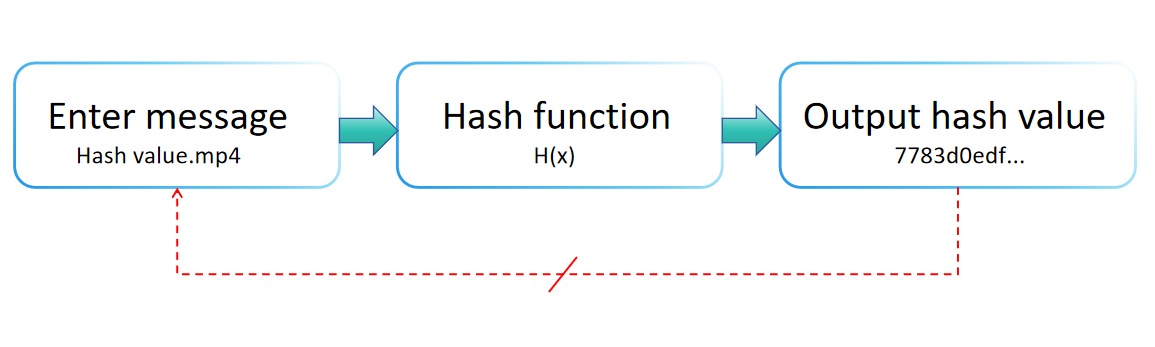
Чувствительность к входу и эффект лавины

В проектировании хеш-функций используются сложные математические и логические операции (такие как битовые операции, операции по модулю и т. д.), чтобы обеспечить высокую чувствительность вывода к вводу. Даже незначительные изменения во входных данных (например, изменение одного бита) приведут к значительным и непредсказуемым изменениям в выводе (хеш-значении), явление, известное как "эффект лавины". [Узнать больше]

Стойкость к коллизиям в криптографии

Стойкость к коллизиям хеш-функции - это важное понятие в криптографии, указывающее на уровень безопасности хеш-функции от атак на коллизии. Это свойство подразумевает, что для любой хеш-функции H нахождение двух различных входов x и y (x ≠ y), таких что H(x) = H(y), вычислительно невозможно. Хеш-функция с надежной стойкостью к коллизиям делает крайне сложным нахождение двух разных входов, приводящих к одному и тому же значению вывода.

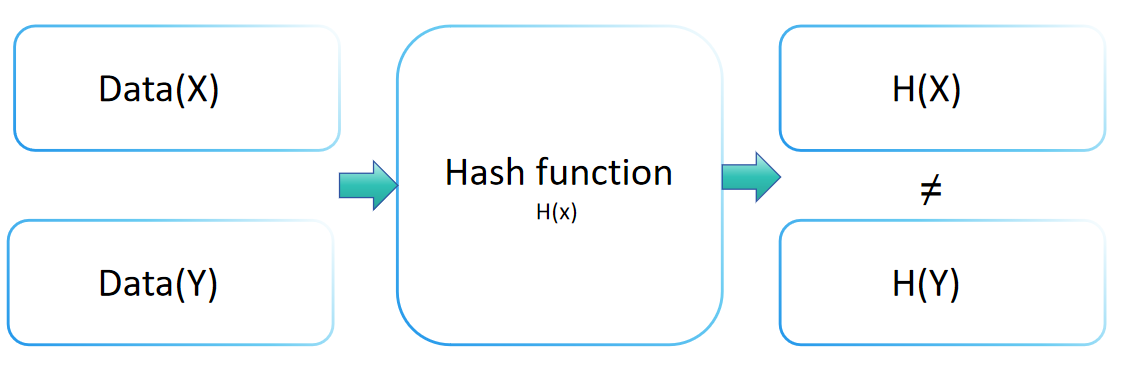
Стойкость к коллизиям играет важную роль в поддержании целостности и проверки данных. Преобразуя входную информацию в фиксированный размер вывода (или дайджест), хеш-функции гарантируют, что никакие два различных входа не произведут одинакового вывода. Это уникальное свойство позволяет идентифицировать исходное значение хеша с высокой точностью.

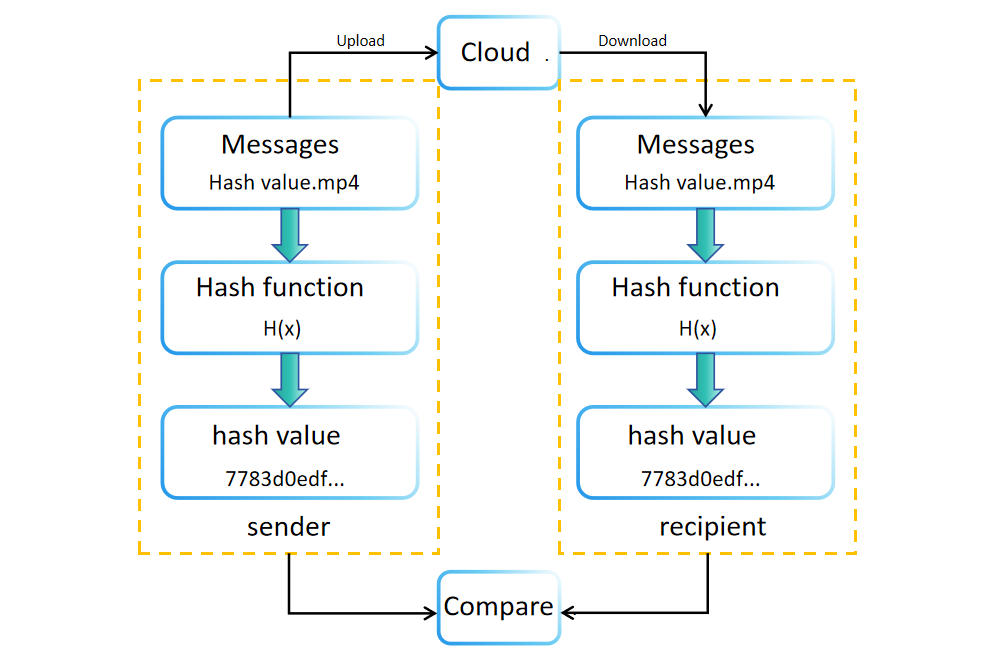
Во время создания или хранения данных создается хеш-значение (или дайджест) с использованием хеш-функции. Это значение хранится или передается вместе с исходными данными. Например, сайты загрузки программного обеспечения часто отображают хеш-значения файлов для проверки целостности. Получатели могут независимо пересчитать хеш-значение полученных данных, чтобы подтвердить их целостность. Если исходное и пересчитанное хеш-значения совпадают, целостность данных подтверждается. В противном случае данные могли быть изменены или повреждены во время передачи или хранения.

Сравнение хеш-значений также предлагает преимущество проверки целостности данных без необходимости большого объема хранения. Этот метод позволяет получателям подтвердить подлинность данных, просто сравнивая хеш-значения до и после передачи.

Могут ли быть найдены коллизии хешей?

Через характеристики вышеупомянутых хеш-функций мы поняли стойкость к коллизиям. Но возможны ли коллизии хешей, то есть, что два разных входа могут дать одинаковый вывод? Ответ утвердительный, коллизии действительно существуют. Согласно принципу джунглей, при достаточно большом пространстве входных данных возможны коллизии хешей. Это происходит потому, что пространство вывода хеш-функций обычно намного меньше пространства входных данных, что неизбежно приводит к тому, что несколько разных входов отображаются на один и тот же вывод.

Принцип джунглей - это простой и интуитивный принцип комбинаторной математики, который гласит, что если более чем n объектов помещаются в n контейнеров, то как минимум один контейнер будет содержать два или более объекта. Этот принцип также может быть использован для объяснения проблем, таких как парадокс дней рождения.

Применение принципа джунглей очень широко, с важным применением в таких областях, как криптография, информатика и математика. Например, в информатике принцип джунглей используется для доказательства корректности определенных алгоритмов или для анализа временной сложности алгоритмов. В криптографии принцип джунглей также используется для разработки определенных методов криптографических атак, таких как атака дня рождения.

Парадокс дней рождения - это классическое применение принципа джунглей. Предположим, в комнате находится n человек. Если мы хотим, чтобы вероятность того, что как минимум два человека делят один и тот же день рождения, была больше 50%, сколько человек нужно? Согласно принципу джунглей, если 367 человек (предполагая, что в году 366 дней, плюс дополнительный день за 29 февраля в високосный год) помещаются в 366 "ящиков" (то есть дни рождения), то как минимум один "ящик" будет содержать двух человек, что означает, что как минимум два человека делят один и тот же день рождения. Это иллюстрирует парадокс дней рождения.

Важно отметить, что хотя принцип джунглей прост и интуитивен, его применение должно учитывать конкретный контекст. Например, при применении принципа джунглей необходимо убедиться, что случайные переменные, вовлеченные в процесс, независимы друг от друга; в противном случае это может привести к неверным выводам. Кроме того, в некоторых случаях также необходимо учитывать такие факторы, как размер и форма ящиков.

Однако попытка найти коллизии хешей путем простого обхода пространства входных данных может оказаться непрактичной, в основном по двум причинам:

• Вычислительная сложность: Для большинства хеш-функций пространство входных данных огромно. Возьмем SHA-256 в качестве примера; его вывод - это 256-битное хеш-значение, что означает, что у него есть 2^256 возможных выводов. Поскольку одной из целей проектирования хеш-функций является минимизация коллизий насколько это возможно, теоретически, нахождение коллизии хеша для SHA-256 потребовало бы обхода около 2^(256/2) = 2^128 входов, согласно парадоксу дней рождения, который является приблизительным ожидаемым количеством входов для нахождения коллизии. Даже с использованием самых мощных суперкомпьютеров, доступных в настоящее время, потребовалось бы гораздо больше времени, чем человеческая жизнь, чтобы выполнить такую задачу. что делает невозможным найти коллизию хеша SHA-256 путем простого обхода.
• Проектирование хеш-функций: Хеш-функции обычно проектируются так, чтобы нахождение коллизий было вычислительно невозможно. Это означает, что, хотя коллизии теоретически существуют, практически их невозможно найти на практике. Это важная характеристика криптографических хеш-функций (таких как SHA-256), которые широко используются в областях цифровых подписей, хранения паролей и многих других.

Конечно, мы также можем использовать специфические алгоритмы для поиска коллизий хешей. Эти алгоритмы часто используют некоторые известные свойства или уязвимости хеш-функций для поиска коллизий. Вот некоторые общие техники и методы для нахождения коллизий хешей:

• Атака дня рождения: Это методика, основанная на вероятности, используемая для оценки времени, необходимого для нахождения коллизии при случайном выборе входных данных. Принцип атаки дня рождения заключается в том, что если в комнате много людей, вероятность того, что два человека будут иметь одинаковый день рождения, увеличивается с увеличением числа людей. Аналогично, в хеш-функциях, если достаточное количество входов выбрано случайным образом, вероятно, что два входа в конечном итоге произведут одинаковый хеш-вывод.
• Атака методом грубой силы: Это самый простой метод, который включает обход всех возможных входов для нахождения коллизии. Однако этот метод непрактичен для хеш-функций с большими пространствами входных данных из-за огромных вычислительных ресурсов и времени, необходимых для этого.
• Радужные таблицы: Этот метод используется для предварительного вычисления и хранения большого количества хеш-значений и соответствующих им входных данных. Радужные таблицы особенно полезны для взлома паролей, которые не использовали обфускацию случайных данных или имеют известную хеш-функцию. Просматривая радужную таблицу, атакующий может быстро найти входные данные, соответствующие определённому хеш-значению.
• Атаки на расширение хеша: Некоторые хеш-функции позволяют злоумышленникам объединять дополнительные данные с известным хеш-значением без знания исходных данных, тем самым генерируя новое хеш-значение. Эта атака может быть использована для конструирования коллизий или выполнения других типов атак.
• Специально сконструированные входные данные: Иногда злоумышленники могут использовать конкретные уязвимости или нелинейные характеристики хеш-функций для создания специальных входных данных, которые более вероятно приведут к коллизиям в хеш-функции.

Какие хеш-функции чаще всего используются?

MD5 (Message Digest Algorithm 5)

MD5 - это широко используемая криптографическая хеш-функция, разработанная Рональдом Ривестом в 1990-х годах для замены старого алгоритма MD4. Она может преобразовывать сообщение любой длины в фиксированное хеш-значение (128 бит, или 16 байт). Цель создания MD5 состояла в том, чтобы обеспечить быстрый и относительно безопасный способ генерации цифрового отпечатка данных. Однако были обнаружены методы коллизий для MD5 , что делает алгоритм небезопасным, но он все еще широко используется в ситуациях, где безопасность не является первостепенной задачей.

Процесс вычисления MD5 включает следующие шаги:

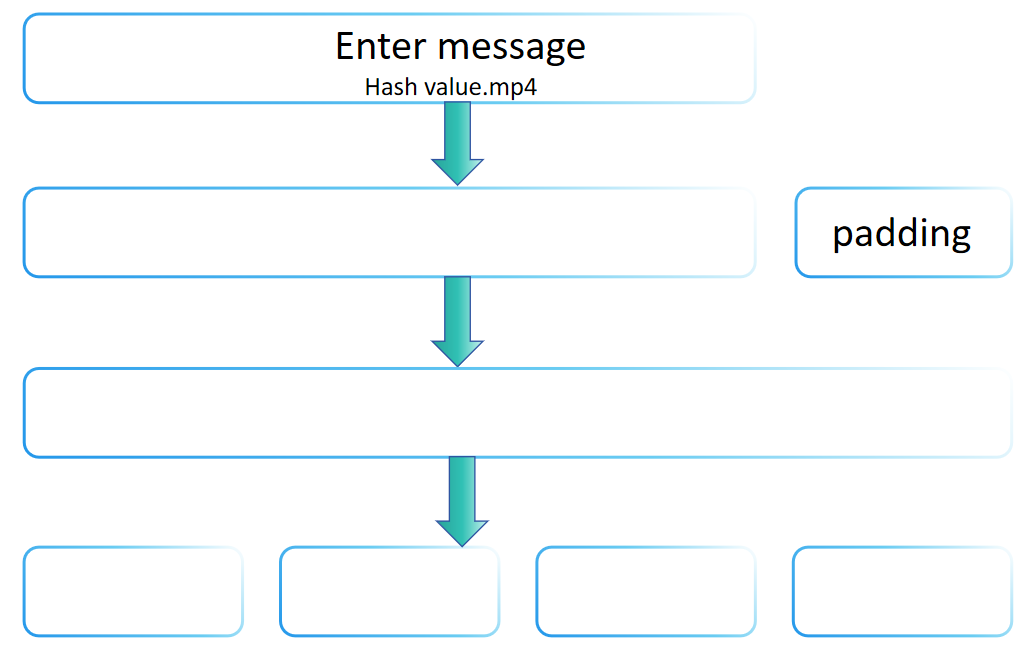
• Дополнение: Исходные данные сначала дополняются так, чтобы их байтовая длина была кратна 512. Дополнение начинается с 1, за которым следуют нули до выполнения требования по длине.
• Добавление длины: К дополненному сообщению добавляется 64-битное значение длины, которое является двоичным представлением длины исходного сообщения, делая окончательную длину сообщения кратной 512 битам.
• Инициализация буфера MD: Четыре 32-битных регистра (A, B, C, D) инициализируются для хранения промежуточных и конечных значений хеша.
• Обработка блоков сообщений: Дополненное и обработанное по длине сообщение делится на блоки по 512 бит, и каждый блок обрабатывается через четыре раунда операций. Каждый раунд включает 16 аналогичных операций на основе нелинейных функций (F, G, H, I), операций циклического сдвига влево и сложения по модулю 32.
• Вывод: Окончательное хеш-значение - это содержимое последнего состояния четырех регистров A, B, C, D, объединенных вместе (каждый регистр имеет 32 бита), образуя 128-битовое хеш-значение.

SHA-1 (Secure Hash Algorithm 1)

SHA-1 был разработан Национальным управлением по безопасности США (NSA) и выпущен в качестве Федерального стандарта обработки информации (FIPS PUB 180-1) Национальным институтом стандартов и технологий (NIST) в 1995 году. SHA-1 предназначен для использования в цифровых подписях и других криптографических приложениях, генерируя 160-битовое (20-байтовое) хеш-значение, известное как хеш-дайджест. Хотя теперь известно, что SHA-1 имеет уязвимости в безопасности и был заменен более безопасными алгоритмами, такими как SHA-256 и SHA-3, понимание его рабочего принципа все еще имеет образовательную и историческую ценность.

Цель создания SHA-1 состоит в том, чтобы взять сообщение произвольной длины и сгенерировать 160-битовый дайджест сообщения для проверки целостности данных. Его процесс вычисления можно разделить на следующие шаги:

• Дополнение: Исходное сообщение сначала дополняется так, чтобы его длина (в битах) по модулю 512 была равна 448. Дополнение всегда начинается с бита "1", за которым следует несколько битов "0", пока не будет выполнено указанное условие по длине.
• Добавление длины: К дополненному сообщению добавляется 64-битный блок, представляющий длину исходного сообщения (в битах), делая окончательную длину сообщения кратной 512 битам.
• Инициализация буфера: Алгоритм SHA-1 использует 160-битный буфер, разделенный на пять 32-битных регистров (A, B, C, D, E), для хранения промежуточных и конечных значений хеша. Эти регистры инициализируются определенными постоянными значениями в начале алгоритма.
• Обработка блоков сообщений: Предварительно обработанное сообщение делится на блоки по 512 бит. Для каждого блока алгоритм выполняет основной цикл, содержащий 80 аналогичных шагов. Эти 80 шагов разделены на четыре раунда, каждый из которых содержит 20 шагов. Каждый шаг использует различную нелинейную функцию (F, G, H, I) и константу (K). Эти функции разработаны для увеличения сложности и безопасности операций. На этих шагах алгоритм использует побитовые операции (например, И, ИЛИ, ИСКЛЮЧАЮЩЕЕ ИЛИ, НЕ) и сложение по модулю 32, а также циклические сдвиги влево.
• Вывод: После обработки всех блоков накопленные значения в пяти регистрах объединяются для формирования окончательного 160-битового хеш-значения.

SHA-2 (Secure Hash Algorithm 2)

SHA-2 - это семейство криптографических хеш-функций, включающее несколько различных версий, в основном состоящее из шести вариантов: SHA-224, SHA-256, SHA-384, SHA-512, SHA-512/224 и SHA-512/256. SHA-2 был разработан Национальным управлением по безопасности США (NSA) и опубликован как Федеральный информационный стандарт (FIPS) Национальным институтом стандартов и технологий (NIST). По сравнению с его предшественником, SHA-1, SHA-2 обеспечивает улучшенную безопасность, в основном отраженную в длинных значениях хеша и более сильной устойчивости к атакам коллизий.

Операция семейства SHA-2 во многом аналогична SHA-1, но обеспечивает более высокую безопасность благодаря использованию длинных значений хеша и более сложной процедуре обработки. Вот основные шаги алгоритма SHA-2:

• Дополнение: Входное сообщение сначала дополняется, чтобы его длина, за вычетом 64 бит, была равна 448 или 896 по модулю 512 (для SHA-224 и SHA-256) или по модулю 1024 (для SHA-384 и SHA-512). Метод дополнения такой же, как и у SHA-1, и включает добавление "1" в конце сообщения, за которым следует несколько "0", и, наконец, двоичное представление длины исходного сообщения в битах в 64 бита (для SHA-224 и SHA-256) или 128 бит (для SHA-384 и SHA-512).
• Инициализация буфера: Алгоритм SHA-2 использует набор инициализированных значений хеша в качестве начального буфера, в зависимости от выбранного варианта SHA-2. Например, SHA-256 использует восемь 32-битных регистров, в то время как SHA-512 использует восемь 64-битных регистров. Эти регистры инициализируются определенными постоянными значениями.
• Обработка блоков сообщений: Дополненное сообщение делится на блоки по 512 или 1024 бита, и каждый блок проходит через несколько раундов криптографических операций. SHA-256 и SHA-224 выполняют 64 раунда операций, в то время как SHA-512, SHA-384, SHA-512/224 и SHA-512/256 выполняют 80 раундов. Каждый раунд операции включает серию сложных побитовых операций, включая логические, модульные сложения и условные операции, основанные на различных нелинейных функциях и предопределенных константах. Эти операции увеличивают сложность и безопасность алгоритма.
• Вывод: Наконец, после обработки всех блоков, значения в буфере объединяются для формирования окончательного хеш-значения. В зависимости от варианта SHA-2, это хеш-значение может быть длиной 224, 256, 384 или 512 бит.

Вас, возможно, интересует, почему вход в хеш-функцию может быть произвольной длины, а выход фиксированной. Причина в том, что семейство SHA-2 использует преобразование Меркла — Дамгарда, которое позволяет создавать хеш-функции, способные обрабатывать сообщения произвольной длины из сжатия функции фиксированной длины. Преобразование Меркла — Дамгарда применяется во многих традиционных хеш-функциях, включая MD5 и SHA-1.

Основная идея преобразования Меркла — Дамгарда заключается в разделении входного сообщения на блоки фиксированного размера, а затем обработке этих блоков один за другим, при этом каждый этап обработки зависит от результата предыдущего, что в конечном итоге приводит к формированию хеш-значения фиксированного размера. Шаг дополнения SHA-256 воплощает основные принципы преобразования Меркла — Дамгарда, то есть путем правильного дополнения для обработки сообщений произвольной длины и обеспечения того, что окончательная обработанная длина сообщения соответствует определенным условиям (например, является кратной фиксированной длине). Поэтому можно сказать, что шаг дополнения SHA-256 следует методу преобразования Меркла — Дамгарда.

Однако SHA-256 не просто прямая реализация преобразования Меркла — Дамгарда. Он также включает в себя серию сложных вычислительных шагов (таких как расширение сообщения, многократные раунды сжатия функций и т. д.), которые являются уникальными конструкциями SHA-256, направленными на повышение его безопасности. Поэтому, хотя SHA-256 следует принципам преобразования Меркла — Дамгарда на этапе дополнения, он повышает общую безопасность путем внедрения других механизмов безопасности, что делает его не ограничивающимся только базовой структурой преобразования Меркла — Дамгарда.

SHA-3 (Secure Hash Algorithm 3)

SHA-3 - последний стандарт безопасного хеширования, официально утвержденный Национальным институтом стандартов и технологий (NIST) в 2015 году как Федеральный информационный стандарт (FIPS 202). SHA-3 не предназначен для замены предыдущих SHA-1 или SHA-2 (поскольку SHA-2 по-прежнему считается безопасным), а скорее для дополнения и предложения альтернативного варианта в семействе SHA, предоставляя другой криптографический алгоритм хеширования. SHA-3 основан на алгоритме Keccak, разработанном Гвидо Бертони и другими, и стал победителем соревнования по SHA-3, проведенного NIST в 2012 году.

Принцип работы SHA-3 существенно отличается от SHA-2, в основном потому, что он использует метод, известный как "конструкция губки", для поглощения и сжатия данных, производя окончательное хеш-значение. Этот метод позволяет SHA-3 гибко выводить хеш-значения разной длины, что обеспечивает более широкий спектр применений по сравнению с SHA-2. Основные этапы SHA-3 следующие:

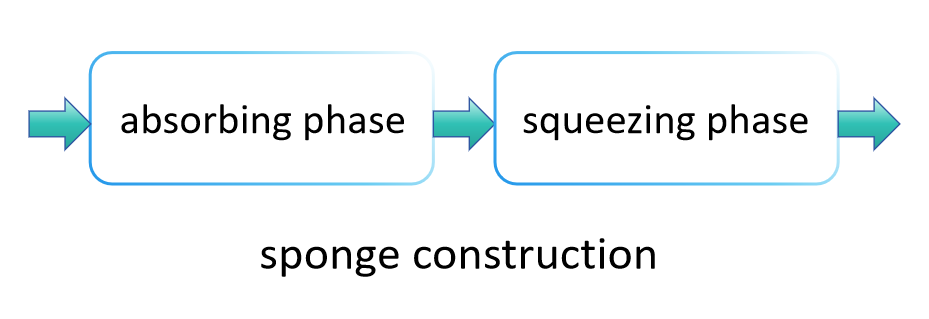
Фаза поглощения:

На этапе поглощения структура губки сначала делит входные данные на блоки фиксированного размера. Эти блоки данных последовательно "поглощаются" во внутреннее состояние губки, которое обычно больше, чем один блок данных, чтобы обеспечить возможность обработки большого объема данных без переполнения. Конкретно, каждый блок данных сливается с частью внутреннего состояния каким-то образом (например, операцией XOR), за которой следует применение фиксированной перестановочной функции (в SHA-3 это Keccak-f), чтобы преобразовать всё состояние, тем самым предотвращая взаимное влияние между различными блоками входных данных. Этот процесс повторяется, пока все блоки входных данных не будут обработаны.

Keccak-f - это основная перестановочная функция, используемая в криптографическом хеш-алгоритме SHA-3. Она является центральным компонентом семейства алгоритмов Keccak. SHA-3 основан на алгоритме Keccak, который победил в конкурсе криптографических хеш-алгоритмов, проведенном NIST, и был выбран в качестве стандарта для SHA-3. Функция Keccak-f имеет несколько вариантов, наиболее часто используемым из которых является Keccak-f[1600], где число указывает на разрядность, на которой она работает.

Keccak-f состоит из множества раундов одинаковых операций (называемых раундами). Для Keccak-f[1600] всего 24 раунда операций. Каждый раунд включает пять базовых шагов: θ (Тета), ρ (Ро), π (Пи), χ (Хи) и ι (Иота). Эти шаги действуют вместе над массивом состояния, постепенно трансформируя его содержимое, увеличивая путаницу и диффузию для повышения безопасности. Ниже краткое описание этих шагов:

• Шаг θ (Тета): Выполняет операции XOR над всеми битами каждого столбца, а затем XOR'ит результат с соседними столбцами, обеспечивая диффузию между столбцами.
• Шаг ρ (Ро): Операция побитового сдвига, при которой каждый бит сдвигается на разное количество битов в соответствии с предопределенными правилами, увеличивая сложность данных.
• Шаг π (Пи): Переупорядочивает биты в массиве состояния, изменяя положение битов для достижения диффузии по строкам и столбцам.
• Шаг χ (Хи): Нелинейный шаг, выполняющий операции XOR над каждым битом каждой строки, включая сам бит, его непосредственного соседа и дополнение соседа. Это локальная операция, которая увеличивает нелинейные характеристики криптографического алгоритма.
• Шаг ι (Иота): Вводит в массив состояния константу раунда, отличающуюся в каждом раунде, чтобы избежать одинаковости всех раундов, вводя непредсказуемость.

Keccak-f обеспечивает высокий уровень безопасности через эти шаги. Его конструкция гарантирует, что даже незначительные изменения во входных данных приводят к широким и непредсказуемым изменениям в массиве состояния, достигаемым через принципы путаницы (сложно для злоумышленников вывести входные данные из вывода) и диффузии (где незначительные изменения во входных данных влияют на несколько частей вывода).

Конструкция Keccak-f позволяет настраивать параметры (такие как размер состояния и количество раундов) в различных уровнях безопасности и сценариях применения, обеспечивая большую гибкость. Keccak-f[1600] известен своей эффективной реализацией, достигая высоких скоростей обработки как в аппаратном, так и в программном обеспечении, особенно при обработке больших объемов данных.

Фаза сжатия:

Как только все блоки входных данных были поглощены во внутреннее состояние, структура губки переходит в фазу сжатия. На этом этапе части внутреннего состояния последовательно выводятся в качестве результата хеш-функции. Если требуемая длина вывода превышает количество данных, которое может быть сжато сразу, структура губки применяет функцию перестановки для снова преобразования внутреннего состояния, затем продолжает выводить больше данных. Этот процесс продолжается, пока не будет достигнута желаемая длина вывода.

Целью дизайна SHA-3 является обеспечение более высокой безопасности по сравнению с SHA-2 и лучшей устойчивости к атакам квантовых вычислений. Благодаря своей уникальной структуре губки, SHA-3 теоретически способен сопротивляться всем текущим известным криптографическим методам атак, включая атаки коллизий, атаки предобразования и вторые атаки предобразования.

RIPEMD-160 (RACE Integrity Primitives Evaluation Message Digest)

RIPEMD-160 - криптографическая хеш-функция, разработанная для обеспечения безопасного алгоритма хеширования. Он был разработан в 1996 году Хансом Доббертином и другими и является членом семейства RIPEMD (RACE Integrity Primitives Evaluation Message Digest).

RIPEMD-160 создает хеш-значение длиной 160 бит (20 байт), что является основой "160" в его названии. Он основан на дизайне MD4 и вдохновлен другими алгоритмами хеширования, такими как MD5 и SHA-1. RIPEMD-160 включает две параллельные, похожие операции, которые обрабатывают входные данные отдельно, а затем объединяют результаты этих двух процессов для генерации конечного хеш-значения. Этот дизайн направлен на увеличение безопасности.

Вычислительный процесс RIPEMD-160 включает несколько основных этапов: дополнение, обработку блоков и сжатие:

• Дополнение: Входное сообщение сначала дополняется, чтобы его длина по модулю 512 бит равнялась 448 битам. Дополнение всегда начинается с одного бита 1, за которым следует серия битов 0, заканчиваясь 64-битным представлением исходной длины сообщения.
• Обработка блоков: Дополненное сообщение разбивается на блоки по 512 бит.
• Инициализация: Используются пять 32-битных регистров (A, B, C, D, E), которые инициализируются определенными конкретными значениями.
• Функция сжатия: Каждый блок обрабатывается поочередно, обновляя значения этих пяти регистров через серию сложных операций. Этот процесс включает побитовые операции (такие как сложение, AND, OR, NOT, кольцевые левые сдвиги) и использование набора фиксированных констант.
• Вывод: После обработки всех блоков значения этих пяти регистров объединяются для формирования конечного хеш-значения длиной 160 бит.