O que é um Valor de Hash?

Um valor de hash é uma cadeia ou número de tamanho fixo gerado a partir de qualquer tamanho de dados de entrada por uma função de hash. Essas funções aceitam entradas diversas como texto, imagens e vídeos, produzindo um valor de hash de comprimento fixo e irreversível. Os valores de hash são determinísticos, o que significa que entradas idênticas sempre resultam na mesma saída. Eles também possuem resistência a colisões, tornando desafiador encontrar entradas distintas que produzam a mesma saída.

Funções do Valor de Hash

Os valores de hash desempenham papéis essenciais em toda a ciência da computação e tecnologia da informação, oferecendo um resumo de tamanho fixo dos dados, independentemente do tamanho. Essas funções facilitam várias aplicações:

• Verificação de Integridade de Dados: Usado para verificar se os dados permanecem inalterados durante a transmissão, garantindo a integridade dos arquivos baixados.
• Armazenamento de Senhas: As senhas são armazenadas como valores de hash para segurança, tornando difícil recuperar senhas originais de bancos de dados comprometidos.
• Recuperação Rápida de Dados: Os valores de hash atuam como índices em tabelas de hash, permitindo operações eficientes com dados.
• Deduplicação de Dados: Ajuda na identificação e remoção de itens de dados duplicados comparando valores de hash.
• Assinatura Digital e Verificação: Garante a integridade e origem dos dados por meio de criptografia de chave pública e funções de hash.
• Tecnologia Blockchain: Utiliza valores de hash para garantir registros de transações e garantir a imutabilidade dos dados.
• Carimbos de Tempo à Prova de Manipulação: Fornece um carimbo de tempo irreversível para dados, útil em proteções legais e de direitos autorais.

A razão pela qual os valores de hash são eficazes nessas áreas é devido às suas características-chave de velocidade, determinismo, irreversibilidade e resistência a colisões. Devidamente utilizadas, as funções de hash podem fornecer suporte robusto na segurança de dados, aumentando a eficiência e verificando a autenticidade das informações.

O que é uma função de hash?

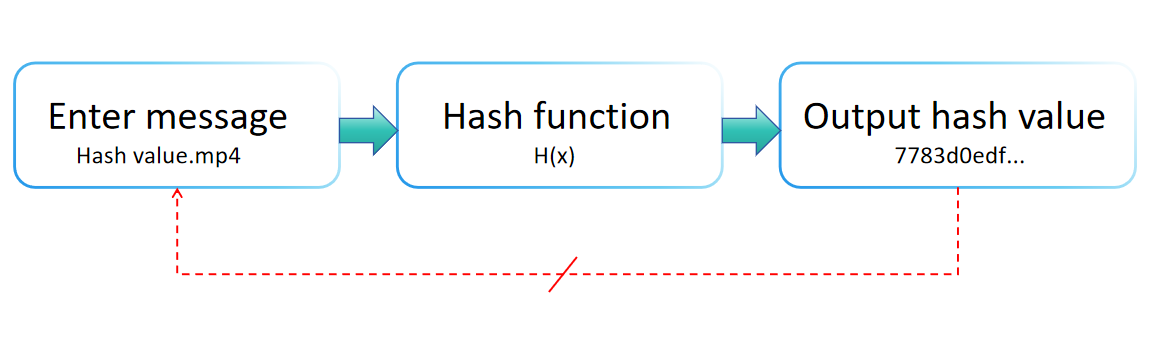
Uma função de hash é uma construção matemática que mapeia dados de entrada (ou "mensagem") para uma cadeia de tamanho fixo, tipicamente um valor numérico, conforme ilustrado no diagrama abaixo. Amplamente utilizado em gerenciamento de dados e segurança da informação, uma função de hash é caracterizada por sua eficiência computacional, comprimento de saída consistente, irreversibilidade, sensibilidade a variações de entrada e resistência a colisões.

Desempenho Computacional Eficiente

As funções de hash podem calcular rapidamente valores de hash a partir de dados de qualquer forma, independentemente do tamanho dos dados. Essa característica é crucial para aplicações que requerem acesso rápido aos dados, como tabelas de hash. Isso ocorre porque, ao armazenar dados em tabelas de hash, a velocidade da função de hash determina a velocidade de recuperação de dados. As tabelas de hash usam funções de hash para localizar rapidamente o local de armazenamento dos dados, dependendo da rápida capacidade computacional das funções de hash.

Além disso, em sistemas que precisam processar grandes quantidades de dados, a eficiência das funções de hash impacta diretamente o desempenho geral do sistema. Se uma função de hash funcionar lentamente, ela se tornará um gargalo no desempenho do sistema. Alguns sistemas em tempo real, como filtragem de pacotes em dispositivos de rede, exigem a computação imediata de valores de hash para dados tomarem decisões rápidas. Nesses casos, a eficiência das funções de hash é igualmente crucial.

Por exemplo, considere uma plataforma de comércio eletrônico online onde os usuários podem digitar nomes de produtos na barra de pesquisa para encontrar produtos. O sistema backend pode usar funções de hash para localizar rapidamente informações de produtos armazenadas em tabelas de hash. Se o processo de cálculo da função de hash for lento, a experiência do usuário será severamente afetada, pois eles terão que esperar mais tempo para obter resultados de pesquisa. Nessa situação, o desempenho computacional eficiente das funções de hash garante tempos de resposta rápidos, melhorando assim a experiência do usuário. [Saiba mais]

Consistência do Comprimento da Saída em Funções de Hash

As funções de hash convertem entradas de qualquer comprimento em uma saída de comprimento fixo por meio de uma série complexa de cálculos. Esse processo frequentemente envolve dividir os dados de entrada em blocos de tamanho fixo (para entradas que excedem o tamanho da unidade de processamento), aplicar uma série de operações matemáticas e lógicas a cada bloco e, em seguida, combinar ou acumular os resultados dessas operações de alguma forma para produzir um valor de hash de tamanho fixo.

Por que é importante? A consistência do comprimento da saída ajuda a garantir a segurança das funções de hash. Se o comprimento da saída do hash pudesse variar, isso poderia vazar informações sobre o tamanho dos dados originais, o que poderia ser potencialmente explorado para atacar o sistema em alguns cenários. Além disso, um comprimento de saída fixo também dificulta que os atacantes inferem características dos dados de entrada analisando o comprimento da saída. Ao mesmo tempo, as saídas de comprimento fixo simplificam o armazenamento e a comparação de valores de hash. Os projetistas de sistemas podem saber com antecedência quanto espaço cada valor de hash ocupará, o que é muito importante para cenários como design de banco de dados e transmissão de rede. Além disso, a consistência do comprimento da saída torna-se muito eficiente para comparar se os valores de hash são iguais, pois requer apenas a comparação de dados de um comprimento fixo. Isso é particularmente importante ao usar tabelas de hash para recuperação rápida de dados.

Tomando SHA-256 como exemplo, esta função de hash criptográfica amplamente utilizada sempre produz um valor de hash de 256 bits (ou seja, 32 bytes), independentemente se os dados de entrada são um único byte ou vários milhões de bytes. Essa consistência garante que os valores de hash SHA-256 possam ser usados para várias aplicações de segurança, como assinaturas digitais e Códigos de Autenticação de Mensagem (MACs), ao mesmo tempo que simplifica o fluxo de trabalho de processamento e armazenamento de dados.

Irreversibilidade das Funções de Hash

As funções de hash são unidirecionais, o que significa que é impossível inferir os dados originais a partir do valor de hash. Esta característica é particularmente importante ao armazenar senhas, pois mesmo que o banco de dados seja comprometido, os atacantes não podem recuperar as senhas a partir dos valores de hash. A irreversibilidade das funções de hash baseia-se principalmente nos seguintes princípios e características:

• Compressão: As funções de hash podem mapear entradas de qualquer tamanho (que podem ser muito grandes em uso prático) para uma saída de tamanho fixo. Isso significa que há infinitamente muitas entradas possíveis mapeadas para um número finito de saídas. Como o espaço de saída (valores de hash) é muito menor que o espaço de entrada, diferentes entradas inevitavelmente produzirão a mesma saída, um fenômeno conhecido como "colisão". Devido a essa compressão, é impossível determinar a entrada específica a partir de uma saída dada (valor de hash).
• Alta Não-linearidade e Complexidade: As funções de hash são projetadas usando operações matemáticas e lógicas complexas (como operações bitwise, operações de módulo, etc.), para garantir que a saída seja altamente sensível à entrada. Mesmo pequenas alterações na entrada (por exemplo, mudar um bit) podem causar mudanças significativas e imprevisíveis na saída (valor de hash). Esse alto grau de não-linearidade e a aleatoriedade da saída tornam extremamente difícil deduzir a entrada original a partir do valor de hash.
• Unidirecionalidade: O design das funções de hash garante que sua operação seja unidirecional; ou seja, enquanto calcular o valor de hash é fácil, o processo reverso (recuperar os dados originais a partir do valor de hash) não é viável. Isso ocorre porque o processo de computação de funções de hash envolve uma série de operações irreversíveis (como a irreversibilidade de operações de módulo), garantindo que mesmo com o valor de hash, seja impossível engenharia reversa dos dados originais.
• Mapeamento Aleatório: Uma função de hash ideal deve atuar como um "mapeador aleatório", o que significa que toda entrada possível tem a mesma probabilidade de ser mapeada para qualquer ponto no espaço de saída. Essa propriedade garante que não há maneira viável de prever para qual saída uma entrada específica será mapeada, aumentando a irreversibilidade da função de hash.
• Fundação Matemática: Matematicamente, a irreversibilidade das funções de hash pode ser entendida através de sua dependência em "problemas de logaritmo discreto", "problemas de fatoração de inteiros grandes" ou outros problemas de teoria dos números que são difíceis de resolver com as capacidades matemáticas e computacionais atuais. Por exemplo, o design de alguns algoritmos de hash pode depender indiretamente da dificuldade computacional desses problemas, garantindo assim sua irreversibilidade.

Sensibilidade à Entrada e o Efeito Avalanche

No design das funções de hash, operações matemáticas e lógicas complexas (como operações bitwise, operações de módulo, etc.) são utilizadas para garantir que a saída seja altamente sensível à entrada. Mesmo pequenas alterações na entrada (por exemplo, mudar um único bit) resultarão em mudanças significativas e imprevisíveis na saída (o valor de hash), um fenômeno conhecido como "efeito avalanche". [Saiba Mais]

Resistência a Colisões em Criptografia

A resistência a colisões de uma função de hash é um conceito crucial em criptografia, indicando o nível de segurança de uma função de hash contra ataques de colisão. Essa propriedade implica que, para qualquer função de hash H, encontrar duas entradas distintas x e y (x ≠ y) tal que H(x) = H(y) é computacionalmente inviável. Uma função de hash com robusta resistência a colisões torna extremamente desafiador encontrar duas entradas diferentes que levem ao mesmo valor de saída.

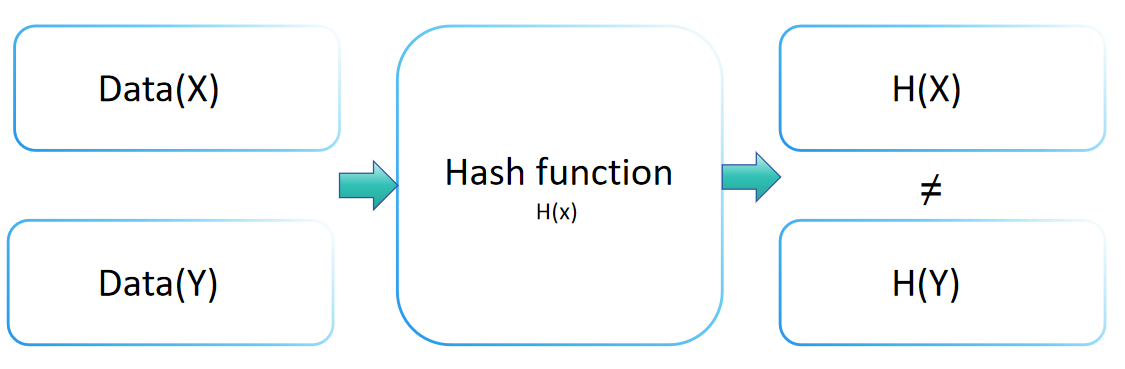
A resistência a colisões desempenha um papel vital na manutenção da integridade e verificação dos dados. Ao transformar informações de entrada em uma saída de tamanho fixo (ou resumo), as funções de hash garantem que duas entradas diferentes não produzam a mesma saída. Essa característica única permite que o valor de hash identifique com precisão o valor original.

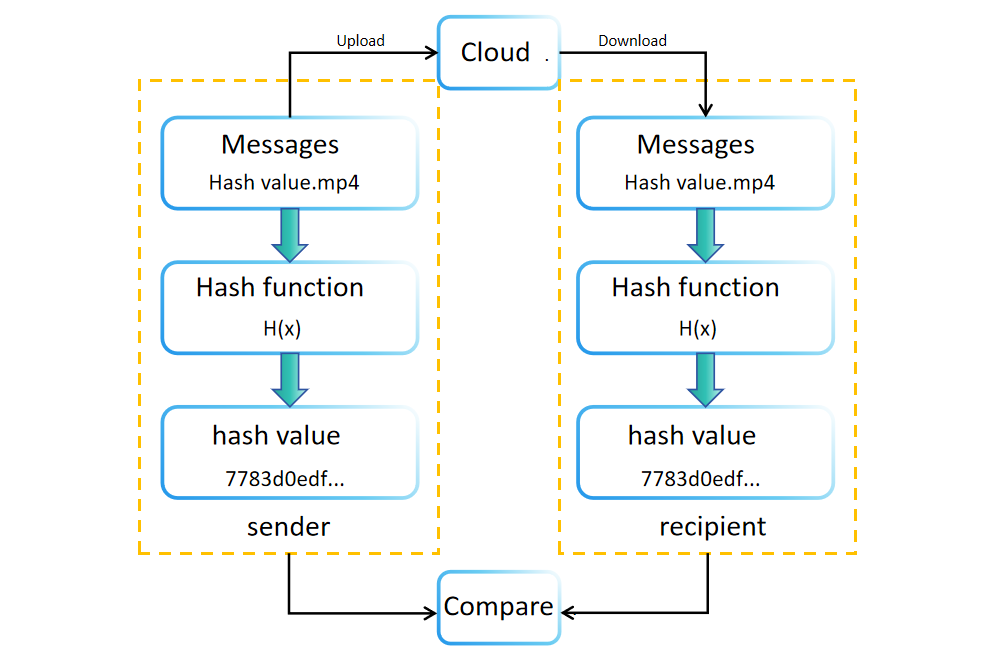
Durante a criação ou armazenamento de dados, um valor de hash (ou resumo) é gerado usando uma função de hash. Este valor é armazenado ou transmitido juntamente com os dados originais. Por exemplo, sites de download de software frequentemente exibem valores de hash de arquivos para verificação de integridade. Os destinatários podem recalcular independentemente o valor de hash dos dados recebidos para confirmar sua integridade. Se os valores de hash original e recalculado coincidirem, a integridade dos dados é verificada. Caso contrário, os dados podem ter sido adulterados ou corrompidos durante a transmissão ou armazenamento.

Comparar valores de hash também oferece a vantagem de verificar a integridade dos dados sem exigir espaço de armazenamento significativo. Este método permite que os destinatários confirmem a autenticidade dos dados simplesmente comparando os valores de hash antes e após a transmissão.

É possível encontrar colisões de hash?

Através das características das funções de hash mencionadas acima, compreendemos a resistência a colisões. Mas é possível que colisões de hash existam, ou seja, que duas entradas diferentes produzam a mesma saída? A resposta é afirmativa, colisões realmente existem. De acordo com o princípio da gaveta de pombos, enquanto o espaço de entrada for suficientemente grande, há uma possibilidade de colisões de hash. Isso ocorre porque o espaço de saída das funções de hash geralmente é muito menor que o espaço de entrada, levando inevitavelmente a múltiplas entradas diferentes mapeadas para a mesma saída.

O princípio da gaveta de pombos é um princípio simples e intuitivo da matemática combinatória, afirmando que se mais do que n objetos forem colocados em n contêineres, então pelo menos um contêiner conterá dois ou mais objetos. Este princípio também pode ser usado para explicar problemas como o paradoxo do aniversário.

A aplicação do princípio da gaveta de pombos é muito ampla, com usos importantes em campos como criptografia, ciência da computação e matemática. Por exemplo, em ciência da computação, o princípio da gaveta de pombos é usado para provar a correção de certos algoritmos ou para analisar a complexidade temporal de algoritmos. Na criptografia, o princípio da gaveta de pombos também é usado para projetar certos métodos de ataque criptográfico, como o ataque do aniversário.

O paradoxo do aniversário é uma aplicação clássica do princípio da gaveta de pombos. Suponha que haja n pessoas em uma sala. Se quisermos que a probabilidade de pelo menos duas pessoas compartilharem o mesmo aniversário seja maior que 50%, quantas pessoas são necessárias? De acordo com o princípio da gaveta de pombos, se 367 pessoas (assumindo que existam 366 dias em um ano, mais um dia extra para 29 de fevereiro em um ano bissexto) forem colocadas em 366 "gavetas de pombos" (ou seja, aniversários), então pelo menos uma "gaveta de pombos" conterá duas pessoas, significando que pelo menos duas pessoas compartilham o mesmo aniversário. Isso ilustra o paradoxo do aniversário.

É importante observar que, embora o princípio da gaveta de pombos seja simples e intuitivo, sua aplicação deve considerar o contexto específico. Por exemplo, ao aplicar o princípio da gaveta de pombos, é necessário garantir que as variáveis aleatórias envolvidas sejam independentes entre si; caso contrário, pode levar a conclusões incorretas. Além disso, em alguns casos, também é necessário considerar fatores como o tamanho e a forma das gavetas de pombos.

No entanto, tentar encontrar colisões de hash simplesmente percorrendo o espaço de entrada pode não ser prático, principalmente por duas razões:

• Complexidade computacional: Para a maioria das funções de hash, o espaço de entrada é vasto. Tome SHA-256 como exemplo; sua saída é um valor de hash de 256 bits, o que significa que possui 2^256 saídas possíveis. Uma vez que um dos objetivos de design das funções de hash é minimizar as colisões tanto quanto possível, teoricamente, encontrar uma colisão de hash para SHA-256 exigiria percorrer cerca de 2^(256/2) = 2^128 entradas, de acordo com o paradoxo do aniversário, que é o número aproximado esperado de entradas para encontrar uma colisão. Mesmo com os supercomputadores mais poderosos atualmente disponíveis, levaria muito além de uma vida humana para concluir uma tarefa dessas. tornando considerado impossível encontrar uma colisão de hash SHA-256 através de uma simples travessia.
• Design de funções de hash: As funções de hash geralmente são projetadas para tornar a descoberta de colisões computacionalmente inviável. Isso significa que, embora as colisões teoricamente existam, elas são praticamente impossíveis de encontrar na prática. Esta é uma característica importante das funções de hash criptográficas (como SHA-256), que são amplamente utilizadas em áreas como assinaturas digitais, armazenamento de senhas e outros.

Claro, também podemos usar algoritmos específicos para tentar encontrar colisões de hash. Esses algoritmos frequentemente exploram algumas propriedades ou fraquezas conhecidas das funções de hash para encontrar colisões. Aqui estão algumas técnicas e métodos comuns para encontrar colisões de hash:

• Ataque do Aniversário: Este é um método simples baseado em probabilidade usado para estimar o tempo necessário para encontrar uma colisão quando as entradas são escolhidas aleatoriamente. O princípio do ataque do aniversário é que se houver muitas pessoas em uma sala, a probabilidade de duas pessoas terem o mesmo aniversário aumenta com o número de pessoas. Da mesma forma, em funções de hash, se um número suficiente de entradas for selecionado aleatoriamente, é provável que duas entradas eventualmente produzam a mesma saída de hash.
• Ataque de Força Bruta: Este é o método mais direto, que envolve percorrer todas as entradas possíveis para encontrar uma colisão. No entanto, este método é impraticável para funções de hash com grandes espaços de entrada devido aos enormes recursos computacionais e tempo necessários.
• Tabelas Arco-Íris: Esta técnica é usada para pré-calcular e armazenar um grande número de valores de hash e suas entradas correspondentes. As tabelas arco-íris são especialmente úteis para quebrar senhas que não utilizaram ofuscação de dados aleatórios ou têm uma função de hash conhecida. Ao procurar na tabela arco-íris, um atacante pode rapidamente encontrar uma entrada que corresponda a um valor de hash específico.
• Ataques de Extensão de Hash: Certas funções de hash permitem que os atacantes combinem dados adicionais com um valor de hash conhecido sem conhecer a entrada original, gerando assim um novo valor de hash. Este ataque pode ser usado para construir colisões ou realizar outros tipos de ataques.
• Entradas Especialmente Construídas: Às vezes, os atacantes podem explorar fraquezas específicas ou comportamentos não lineares em funções de hash para construir entradas especiais que são mais propensas a produzir colisões na função de hash.

Quais são as funções de hash comumente usadas?

MD5 (Message Digest Algorithm 5)

MD5 é uma função de hash criptográfica amplamente utilizada, projetada por Ronald Rivest na década de 1990 para substituir o antigo algoritmo MD4. Ele pode converter uma mensagem de qualquer comprimento em um valor de hash de comprimento fixo (128 bits, ou 16 bytes). O objetivo de design do MD5 era fornecer uma maneira rápida e relativamente segura de gerar uma impressão digital digital de dados. No entanto, foram descobertos métodos de colisão para MD5 , tornando o algoritmo inseguro, mas ainda amplamente utilizado em situações onde a segurança não é uma preocupação primária.

O processo de cálculo do MD5 envolve as seguintes etapas:

• Preenchimento: Inicialmente, os dados originais são preenchidos para que seu comprimento em bytes seja um múltiplo de 512. O preenchimento começa com um 1, seguido de 0s até que o requisito de comprimento seja atendido.
• Adição de Comprimento: Um valor de comprimento de 64 bits, que é a representação binária do comprimento da mensagem original, é adicionado à mensagem preenchida, tornando o comprimento final da mensagem um múltiplo de 512 bits.
• Inicialização do Buffer MD: Quatro registradores de 32 bits (A, B, C, D) são inicializados para armazenar os valores de hash intermediários e finais.
• Processamento de Blocos de Mensagem: A mensagem preenchida e processada em termos de comprimento é dividida em blocos de 512 bits, e cada bloco é processado através de quatro rodadas de operação. Cada rodada inclui 16 operações semelhantes baseadas em funções não lineares (F, G, H, I), operações de deslocamento circular à esquerda e adição módulo 32.
• Saída: O valor de hash final é o conteúdo do último estado dos quatro registradores A, B, C, D concatenados juntos (cada registro tem 32 bits), formando um valor de hash de 128 bits.

SHA-1 (Secure Hash Algorithm 1)

SHA-1 foi projetado pela Agência de Segurança Nacional dos Estados Unidos (NSA) e lançado como um Padrão de Processamento de Informações Federais (FIPS PUB 180-1) pelo Instituto Nacional de Padrões e Tecnologia (NIST) em 1995. SHA-1 destina-se a ser utilizado em assinaturas digitais e outras aplicações criptográficas, gerando um valor de hash de 160 bits (20 bytes) conhecido como digest de mensagem. Embora seja agora conhecido que SHA-1 tem vulnerabilidades de segurança e foi substituído por algoritmos mais seguros como SHA-256 e SHA-3, entender seu princípio de funcionamento ainda possui valor educacional e histórico.

O propósito de design do SHA-1 é pegar uma mensagem de comprimento arbitrário e produzir um digest de mensagem de 160 bits para verificar a integridade dos dados. Seu processo de computação pode ser dividido nas seguintes etapas:

• Preenchimento: Inicialmente, a mensagem original é preenchida para que seu comprimento (em bits) módulo 512 seja igual a 448. O preenchimento sempre começa com um bit "1", seguido por vários bits "0", até que a condição de comprimento acima seja atendida.
• Adição de Comprimento: Um bloco de 64 bits é adicionado à mensagem preenchida, representando o comprimento da mensagem original (em bits), tornando o comprimento final da mensagem um múltiplo de 512 bits.
• Inicialização do Buffer: O algoritmo SHA-1 usa um buffer de 160 bits, dividido em cinco registradores de 32 bits (A, B, C, D, E), para armazenar os valores de hash intermediários e finais. Esses registradores são inicializados com valores constantes específicos no início do algoritmo.
• Processamento de Blocos de Mensagem: A mensagem pré-processada é dividida em blocos de 512 bits. Para cada bloco, o algoritmo executa um loop principal contendo 80 etapas semelhantes. Essas 80 etapas são divididas em quatro rodadas, cada uma com 20 etapas. Cada etapa usa uma função não linear diferente (F, G, H, I) e uma constante (K). Essas funções são projetadas para aumentar a complexidade e segurança das operações. Nestas etapas, o algoritmo usa operações bitwise (como AND, OR, XOR, NOT) e adição módulo 32, bem como deslocamentos circulares à esquerda.
• Saída: Após processar todos os blocos, os valores acumulados nos cinco registradores são concatenados para formar o valor de hash final de 160 bits.

SHA-2 (Secure Hash Algorithm 2)

SHA-2 é uma família de funções de hash criptográficas, incluindo várias versões diferentes, consistindo principalmente de seis variantes: SHA-224, SHA-256, SHA-384, SHA-512, SHA-512/224 e SHA-512/256. SHA-2 foi projetado pela Agência de Segurança Nacional dos Estados Unidos (NSA) e publicado como um Padrão Federal de Processamento de Informações (FIPS) pelo Instituto Nacional de Padrões e Tecnologia (NIST). Comparado ao seu antecessor, SHA-1, SHA-2 oferece segurança aprimorada, principalmente refletida em valores de hash mais longos e maior resistência a ataques de colisão.

O funcionamento da família SHA-2 é semelhante ao SHA-1 em muitos aspectos, mas fornece maior segurança através do uso de valores de hash mais longos e um procedimento de processamento mais complexo. Aqui estão as principais etapas do algoritmo SHA-2:

• Preenchimento: A mensagem de entrada é primeiro preenchida para que seu comprimento, menos 64 bits, seja igual a 448 ou 896 em uma base módulo 512 (para SHA-224 e SHA-256) ou módulo 1024 (para SHA-384 e SHA-512). O método de preenchimento é o mesmo que o SHA-1, que envolve adicionar um "1" no final da mensagem, seguido por vários "0"s, e finalmente uma representação binária de 64 bits (para SHA-224 e SHA-256) ou 128 bits (para SHA-384 e SHA-512) do comprimento original da mensagem em bits.
• Inicialização do Buffer: O algoritmo SHA-2 usa um conjunto de valores de hash inicializados como o buffer de início, dependendo da variante SHA-2 escolhida. Por exemplo, SHA-256 usa oito registradores de 32 bits, enquanto SHA-512 usa oito registradores de 64 bits. Esses registradores são inicializados com valores constantes específicos.
• Processamento de Blocos de Mensagem: A mensagem preenchida é dividida em blocos de 512 ou 1024 bits, e cada bloco passa por múltiplas rodadas de operações criptográficas. SHA-256 e SHA-224 realizam 64 rodadas de operações, enquanto SHA-512, SHA-384, SHA-512/224 e SHA-512/256 realizam 80 rodadas. Cada rodada de operação inclui uma série de operações bitwise complexas, incluindo operações lógicas, adição modular e condicional, baseadas em diferentes funções não lineares e constantes predefinidas. Essas operações aumentam a complexidade e a segurança do algoritmo.
• Saída: Finalmente, após processar todos os blocos, os valores no buffer são combinados para formar o valor de hash final. Dependendo da variante SHA-2, este valor de hash pode ter 224, 256, 384 ou 512 bits de comprimento.

Você pode estar curioso para saber por que a entrada para uma função de hash pode ter um comprimento arbitrário, mas a saída é fixa. A razão é que a família SHA-2 usa a transformação Merkle-Damgård, que permite a construção de funções de hash que podem processar mensagens de qualquer comprimento a partir de uma função de compressão de comprimento fixo. A transformação Merkle-Damgård é adotada em muitas funções de hash tradicionais, incluindo MD5 e SHA-1.

A ideia central da transformação Merkle-Damgård é dividir a mensagem de entrada em blocos de tamanho fixo e, em seguida, processar esses blocos um por um, com cada etapa de processamento dependendo do resultado da anterior, produzindo finalmente um valor de hash de tamanho fixo. A etapa de preenchimento do SHA-256 incorpora os princípios básicos da transformação Merkle-Damgård, ou seja, preenchendo adequadamente para processar mensagens de qualquer comprimento e garantindo que o comprimento da mensagem processada final atenda a certas condições (como ser um múltiplo de um comprimento fixo). Portanto, pode-se dizer que a etapa de preenchimento do SHA-256 segue o método de transformação Merkle-Damgård.

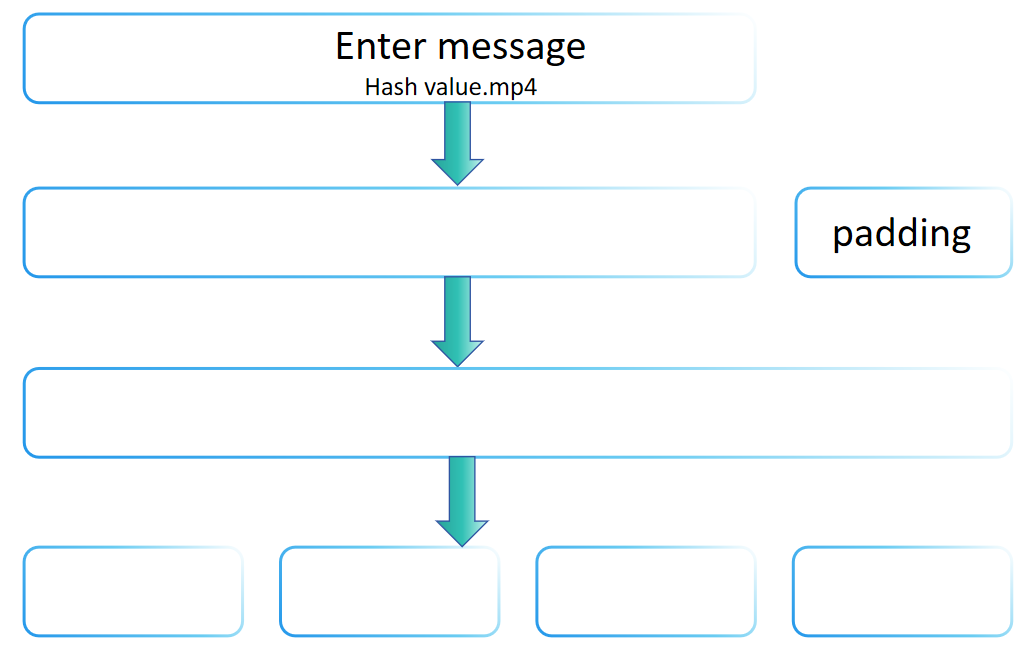
No entanto, o SHA-256 não é apenas uma implementação direta da transformação Merkle-Damgård. Ele também inclui uma série de etapas computacionais complexas (como expansão de mensagem, múltiplas rodadas de funções de compressão, etc.), que são designs exclusivos do SHA-256, com o objetivo de melhorar sua segurança. Portanto, embora o SHA-256 siga os princípios da transformação Merkle-Damgård em sua etapa de preenchimento, ele aumenta a segurança geral introduzindo outros mecanismos de segurança, tornando-o não apenas limitado ao esquema básico da transformação Merkle-Damgård.

SHA-3 (Secure Hash Algorithm 3)

SHA-3 é o mais recente padrão de hash seguro, oficialmente aprovado pelo Instituto Nacional de Padrões e Tecnologia (NIST) em 2015 como um Padrão Federal de Processamento de Informações (FIPS 202). SHA-3 não se destina a substituir o SHA-1 ou SHA-2 anteriores (já que o SHA-2 ainda é considerado seguro), mas sim complementar e oferecer uma opção alternativa dentro da família SHA, fornecendo um algoritmo de hash criptográfico diferente. SHA-3 é baseado no algoritmo Keccak, projetado por Guido Bertoni e outros, e foi o vencedor da competição SHA-3 realizada pelo NIST em 2012.

O princípio de funcionamento do SHA-3 difere significativamente do SHA-2, principalmente porque utiliza um método conhecido como "construção de esponja" para absorver e espremer dados, produzindo o valor de hash final. Este método permite ao SHA-3 produzir flexivelmente valores de hash de diferentes comprimentos, oferecendo assim uma gama mais ampla de aplicações do que o SHA-2. As principais etapas do SHA-3 são as seguintes:

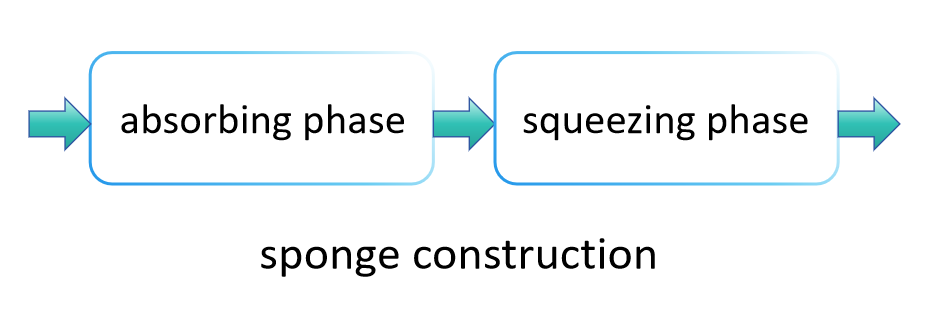
Fase de absorção:

Na fase de absorção, a estrutura de esponja divide primeiro os dados de entrada em blocos de tamanho fixo. Esses blocos de dados são "absorvidos" sequencialmente no estado interno da esponja, que é tipicamente maior do que um único bloco de dados, para garantir que uma grande quantidade de dados possa ser processada sem transbordamento. Especificamente, cada bloco de dados é mesclado com uma parte do estado interno de alguma maneira (como por uma operação XOR), seguido pela aplicação de uma função de permutação fixa (no SHA-3, isso é Keccak-f) para transformar o estado inteiro, evitando assim a interferência entre diferentes blocos de dados de entrada. Esse processo é repetido até que todos os blocos de dados de entrada tenham sido processados.

Keccak-f é a função de permutação central usada no algoritmo de hash criptográfico SHA-3. É um componente central da família de algoritmos Keccak. O SHA-3 é baseado no algoritmo Keccak, que venceu a competição de algoritmos de hash criptográfico realizada pelo NIST e foi selecionado como o padrão para o SHA-3. A função Keccak-f tem várias variantes, sendo a mais comumente usada a Keccak-f[1600], onde o número indica a largura de bits em que opera.

Keccak-f é composto por várias rodadas da mesma operação (chamadas de rodadas). Para Keccak-f[1600], há um total de 24 rodadas de operações. Cada rodada inclui cinco etapas básicas: θ (Theta), ρ (Rho), π (Pi), χ (Chi) e ι (Iota). Essas etapas atuam em conjunto no array de estado, transformando gradualmente seu conteúdo, aumentando a confusão e a difusão para aumentar a segurança. Abaixo está uma breve descrição dessas etapas:

• Etapa θ (Theta): Realiza operações XOR em todos os bits de cada coluna, em seguida, XORs o resultado em colunas adjacentes, fornecendo difusão entre colunas.
• Etapa ρ (Rho): Operação de rotação de bits, onde cada bit é rotacionado um número diferente de bits de acordo com regras predeterminadas, aumentando a complexidade dos dados.
• Etapa π (Pi): Rearranja os bits no array de estado, mudando a posição dos bits para alcançar difusão entre linhas e colunas.
• Etapa χ (Chi): Uma etapa não linear que realiza operações XOR em cada bit de cada linha, incluindo ele mesmo, seu vizinho imediato e o complemento do vizinho. Esta é uma operação local que aumenta as características não lineares do algoritmo criptográfico.
• Etapa ι (Iota): Introduz uma constante de rodada em parte do array de estado, com a constante diferindo em cada rodada, para evitar que todas as rodadas operem de forma idêntica, introduzindo imprevisibilidade.

Keccak-f fornece um alto nível de segurança através dessas etapas. Seu design garante que mesmo mudanças mínimas na entrada levem a mudanças generalizadas e imprevisíveis no array de estado, alcançado através dos princípios de confusão (tornando difícil para os atacantes inferir a entrada a partir da saída) e difusão (onde mudanças mínimas na entrada afetam várias partes da saída).

O design de Keccak-f permite o ajuste de parâmetros (como tamanho de estado e número de rodadas) em diferentes níveis de segurança e cenários de aplicação, oferecendo grande flexibilidade. Keccak-f[1600] é renomado por sua implementação eficiente, alcançando altas velocidades de processamento tanto em hardware quanto em software, especialmente ao lidar com grandes quantidades de dados.

Fase de Espremer:

Uma vez que todos os blocos de dados de entrada foram absorvidos no estado interno, a estrutura de esponja entra na fase de espremer. Nesta etapa, partes do estado interno são progressivamente produzidas como resultado da função de hash. Se o comprimento de saída necessário exceder a quantidade que pode ser espremida de uma vez, a estrutura de esponja aplica a função de permutação para transformar o estado interno novamente e depois continua a produzir mais dados. Este processo é realizado até que o comprimento de saída desejado seja alcançado.

O objetivo do design do SHA-3 é fornecer uma segurança mais alta do que o SHA-2 e uma melhor resistência contra ataques de computação quântica. Graças à sua estrutura de esponja única, o SHA-3 é teoricamente capaz de resistir a todos os métodos de ataque criptográfico atualmente conhecidos, incluindo ataques de colisão, ataques de pré-imagem e ataques de segunda pré-imagem.

RIPEMD-160 (RACE Integrity Primitives Evaluation Message Digest)

RIPEMD-160 é uma função de hash criptográfica projetada para fornecer um algoritmo de hash seguro. Foi desenvolvido em 1996 por Hans Dobbertin e outros, e é membro da família RIPEMD (RACE Integrity Primitives Evaluation Message Digest).

RIPEMD-160 produz um valor de hash de 160 bits (20 bytes), que é a origem do "160" em seu nome. É baseado no design de MD4 e influenciado por outros algoritmos de hash como MD5 e SHA-1. RIPEMD-160 inclui duas operações paralelas e semelhantes que processam os dados de entrada separadamente e depois combinam os resultados desses dois processos para gerar o valor de hash final. Este design visa aumentar a segurança.

O processo de computação do RIPEMD-160 inclui várias etapas básicas: preenchimento, processamento de bloco e compressão:

• Preenchimento: A mensagem de entrada é primeiro preenchida para garantir que seu comprimento módulo 512 bits seja igual a 448 bits. O preenchimento sempre começa com um único bit de 1 seguido de uma série de bits 0, terminando com uma representação de 64 bits do comprimento da mensagem original.
• Processamento de Bloco: A mensagem preenchida é dividida em blocos de 512 bits.
• Inicialização: Usa cinco registros de 32 bits (A, B, C, D, E), que são inicializados com valores específicos.
• Função de Compressão: Cada bloco é processado por vez, atualizando os valores desses cinco registros por meio de uma série de operações complexas. Este processo inclui operações bitwise (como adição, AND, OR, NOT, deslocamentos circulares para a esquerda) e o uso de um conjunto de constantes fixas.
• Saída: Após todos os blocos terem sido processados, os valores desses cinco registros são concatenados para formar o valor de hash final de 160 bits.