Wat is een Hash Waarde?

Een hash waarde is een vaste grootte string of nummer gegenereerd vanuit elk formaat van invoergegevens door een hashfunctie. Deze functies accepteren diverse invoeren zoals tekst, afbeeldingen en video's, waarbij een vaste lengte, onomkeerbare hash waarde wordt geproduceerd. Hash waarden zijn deterministisch, wat betekent dat identieke invoeren altijd hetzelfde resultaat opleveren. Ze beschikken ook over collision resistance, waardoor het moeilijk is om verschillende invoeren te vinden die hetzelfde resultaat opleveren.

Functies van Hash Waarde

Hash waarden vervullen essentiële rollen in de informatica en IT, door een vaste lengte samenvatting van gegevens te bieden, ongeacht de grootte. Deze functies vergemakkelijken diverse toepassingen:

• Verificatie van Data Integriteit: Gebruikt om te controleren of gegevens ongewijzigd blijven tijdens transmissie, om de integriteit van gedownloade bestanden te waarborgen.
• Opslag van Wachtwoorden: Wachtwoorden worden opgeslagen als hash waarden voor beveiliging, waardoor het moeilijk wordt om originele wachtwoorden te herstellen uit gecompromitteerde databases.
• Snelle Data Ophaling: Hash waarden fungeren als indices in hash tabellen, waardoor efficiënte data operaties mogelijk zijn.
• Data Deduplicatie: Helpt bij het identificeren en verwijderen van dubbele data items door het vergelijken van hash waarden.
• Digitale Handtekening en Verificatie: Zorgt voor data integriteit en herkomst door middel van publieke sleutel cryptografie en hash functies.
• Blockchain Technologie: Gebruikt hash waarden om transactierecords te beveiligen en data onveranderlijkheid te waarborgen.
• Onvervalsbaar Tijdstempels: Voorziet een onomkeerbare tijdstempel voor data, nuttig in juridische en auteursrechten bescherming.

De reden dat hash waarden effectief zijn in deze gebieden is vanwege hun sleutelkenmerken van snelheid, determinisme, onomkeerbaarheid en collision resistance. Correct gebruikt, kunnen hash functies robuuste ondersteuning bieden in het beveiligen van data, het verhogen van de efficiëntie, en het verifiëren van de authenticiteit van informatie.

Wat is een Hashfunctie?

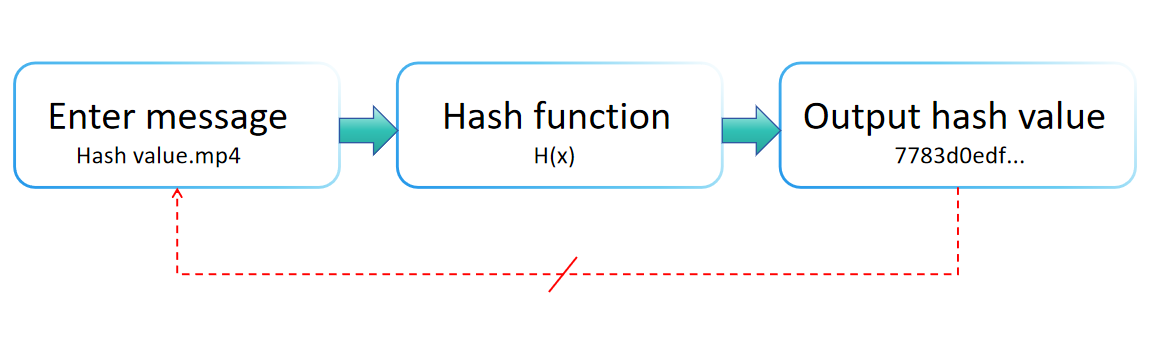
Een hashfunctie is een wiskundige constructie die invoergegevens (of "bericht") in kaart brengt naar een vaste grootte string, typisch een numerieke waarde, zoals geïllustreerd in de onderstaande diagram. Breed gebruikt in gegevensbeheer en informatiebeveiliging, wordt een hashfunctie gekenmerkt door zijn efficiënte computationele prestaties, consistente uitvoerlengte, onomkeerbaarheid, gevoeligheid voor invoervariaties, en weerstand tegen botsingen.

Efficiënte Computationele Prestaties

Hashfuncties kunnen snel hashwaarden berekenen van gegevens in elke vorm, ongeacht de grootte van de gegevens. Deze eigenschap is cruciaal voor toepassingen die snelle toegang tot gegevens vereisen, zoals hashtabellen. Dit komt omdat, wanneer gegevens in hashtabellen worden opgeslagen, de snelheid van de hashfunctie de snelheid van gegevensopvraging bepaalt. Hashtabellen gebruiken hashfuncties om snel de opslaglocatie van de gegevens te vinden, waarbij ze vertrouwen op de snelle computationele capaciteit van hashfuncties.

Bovendien, in systemen die grote hoeveelheden gegevens moeten verwerken, heeft de efficiëntie van hashfuncties directe impact op de algehele systeemprestaties. Als een hashfunctie langzaam werkt, zal het een knelpunt in systeemprestaties worden. Sommige real-time systemen, zoals pakketfiltering in netwerkapparaten, vereisen onmiddellijke berekening van hashwaarden voor gegevens om snel beslissingen te nemen. In deze gevallen is de efficiëntie van hashfuncties even cruciaal.

Neem bijvoorbeeld een online e-commerce platform waar gebruikers productnamen in de zoekbalk kunnen invoeren om producten te vinden. Het backend systeem kan hashfuncties gebruiken om snel productinformatie opgeslagen in hashtabellen te lokaliseren. Als het berekeningsproces van de hashfunctie traag is, zal de gebruikerservaring ernstig worden beïnvloed, omdat ze langer moeten wachten om zoekresultaten te krijgen. In deze situatie zorgt de efficiënte computationele prestatie van hashfuncties voor snelle reactietijden, waardoor de gebruikerservaring verbetert. [Kom meer te weten]

Consistentie van de Uitvoerlengte in Hashfuncties

Hashfuncties zetten invoer van elke lengte om in een uitvoer met een vaste lengte door een complexe reeks berekeningen. Dit proces omvat vaak het verdelen van de invoergegevens in blokken van vaste grootte (voor die invoeren die de grootte van de verwerkingseenheid overschrijden), het toepassen van een reeks wiskundige en logische operaties op elk blok, en vervolgens op een bepaalde manier combineren of accumuleren van de resultaten van deze operaties om uiteindelijk een hashwaarde met een vaste grootte te produceren.

Waarom is het belangrijk? De consistentie van de uitvoerlengte helpt de veiligheid van hashfuncties te waarborgen. Als de lengte van de hashuitvoer zou kunnen variëren, zou dit informatie kunnen lekken over de grootte van de oorspronkelijke gegevens, wat potentieel zou kunnen worden gebruikt om het systeem in sommige scenario's aan te vallen. Bovendien maakt een vaste uitvoerlengte het ook moeilijk voor aanvallers om kenmerken van de invoergegevens af te leiden door de uitvoerlengte te analyseren. Tegelijkertijd vereenvoudigen uitvoeren met een vaste lengte de opslag en vergelijking van hashwaarden. Systeemontwerpers kunnen van tevoren weten hoeveel ruimte elke hashwaarde in beslag zal nemen, wat erg belangrijk is voor scenario's zoals databaseontwerp en netwerktransmissie. Verder wordt de consistentie van de uitvoerlengte zeer efficiënt voor het vergelijken of hashwaarden gelijk zijn omdat het alleen het vergelijken van gegevens van een vaste lengte vereist. Dit is vooral belangrijk bij het gebruik van hashtabellen voor snelle gegevensopvraging.

SHA-256 als voorbeeld nemend, produceert deze veelgebruikte cryptografische hashfunctie altijd een 256-bits (d.w.z. 32-byte) hashwaarde, ongeacht of de invoergegevens één byte of enkele miljoenen bytes zijn. Deze consistentie zorgt ervoor dat SHA-256 hashwaarden kunnen worden gebruikt voor verschillende beveiligingstoepassingen, zoals digitale handtekeningen en Message Authentication Codes (MAC's), terwijl het de workflow van gegevensverwerking en -opslag vereenvoudigt.

Onomkeerbaarheid van Hashfuncties

Hashfuncties zijn unidirectioneel, wat betekent dat het onmogelijk is om de originele gegevens vanuit de hashwaarde te achterhalen. Deze eigenschap is vooral belangrijk bij het opslaan van wachtwoorden, aangezien zelfs als de database gecompromitteerd is, aanvallers de wachtwoorden niet kunnen herstellen vanuit de hashwaarden. De onomkeerbaarheid van hashfuncties is voornamelijk gebaseerd op de volgende principes en kenmerken:

• Compressie: Hashfuncties kunnen invoer van elke lengte (die in de praktijk erg groot kan zijn) omzetten naar een uitvoer van vaste lengte. Dit betekent dat er oneindig veel mogelijke invoeren zijn die naar een eindig aantal uitvoeren worden gemapt. Aangezien de uitvoerruimte (hashwaarden) veel kleiner is dan de invoerruimte, zullen verschillende invoeren onvermijdelijk dezelfde uitvoer produceren, een fenomeen dat bekend staat als een "botsing." Door deze compressie is het onmogelijk om de specifieke invoer van een gegeven uitvoer (hashwaarde) te bepalen.
• Hoge Non-lineariteit en Complexiteit: Hashfuncties zijn ontworpen met behulp van complexe wiskundige en logische operaties (zoals bitwise operaties, modulo operaties, etc.), om ervoor te zorgen dat de uitvoer zeer gevoelig is voor de invoer. Zelfs kleine wijzigingen in de invoer (bijvoorbeeld het veranderen van één bit) kunnen significante en onvoorspelbare veranderingen in de uitvoer (hashwaarde) veroorzaken. Deze hoge mate van non-lineariteit en de willekeur van de uitvoer maken het uiterst moeilijk om de originele invoer vanuit de hashwaarde af te leiden.
• Unidirectionality: Het ontwerp van hashfuncties zorgt ervoor dat hun werking eenrichtingsverkeer is; dat wil zeggen, terwijl het berekenen van de hashwaarde eenvoudig is, is het omgekeerde proces (het herstellen van de originele gegevens vanuit de hashwaarde) niet haalbaar. Dit komt omdat het berekeningsproces van hashfuncties een reeks onomkeerbare operaties omvat (zoals de onomkeerbaarheid van modulo operaties), ervoor zorgend dat zelfs met de hashwaarde, het onmogelijk is om de originele gegevens reverse-engineeren.
• Willekeurige Mapping: Een ideale hashfunctie zou moeten fungeren als een "willekeurige mapper," wat betekent dat elke mogelijke invoer even waarschijnlijk is om naar elk punt in de uitvoerruimte te worden gemapt. Deze eigenschap zorgt ervoor dat er geen haalbare manier is om te voorspellen naar welke uitvoer een specifieke invoer zal worden gemapt, waardoor de onomkeerbaarheid van de hashfunctie wordt versterkt.
• Wiskundige Basis: Wiskundig kan de onomkeerbaarheid van hashfuncties worden begrepen door hun afhankelijkheid van "discrete logaritmeproblemen," "problemen met het factoriseren van grote gehele getallen," of andere getaltheorieproblemen die moeilijk op te lossen zijn met de huidige wiskundige en computationele capaciteiten. Bijvoorbeeld, het ontwerp van sommige hashalgoritmen kan indirect afhankelijk zijn van de computationele moeilijkheid van deze problemen, waardoor hun onomkeerbaarheid wordt gewaarborgd.

Gevoeligheid van Invoer en het Sneeuwbaleffect

Bij het ontwerpen van hashfuncties worden complexe wiskundige en logische operaties (zoals bitwise operaties, modulo operaties, etc.) gebruikt om ervoor te zorgen dat de uitvoer zeer gevoelig is voor de invoer. Zelfs kleine wijzigingen in de invoer (bijvoorbeeld het wijzigen van een enkele bit) zullen resulteren in significante en onvoorspelbare veranderingen in de uitvoer (de hashwaarde), een fenomeen dat bekend staat als het “sneeuwbaleffect”. [Kom meer te weten]

Botsingsbestendigheid in Cryptografie

De botsingsbestendigheid van een hashfunctie is een cruciaal concept in de cryptografie, dat het beveiligingsniveau van een hashfunctie tegen botsingsaanvallen aangeeft. Deze eigenschap impliceert dat voor elke hashfunctie H, het vinden van twee verschillende invoeren x en y (x ≠ y) zodanig dat H(x) = H(y) rekenkundig onuitvoerbaar is. Een hashfunctie met robuuste botsingsbestendigheid maakt het uiterst uitdagend om twee verschillende invoeren te vinden die leiden tot dezelfde uitvoerwaarde.

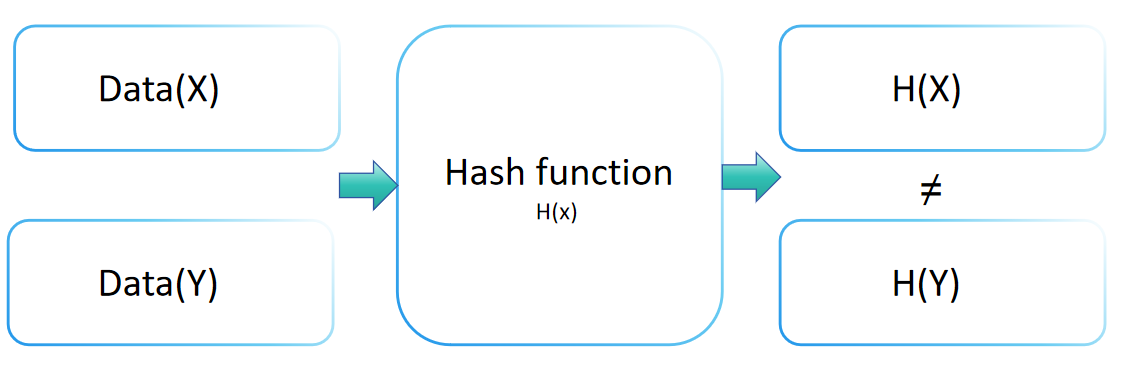
Botsingsbestendigheid speelt een vitale rol bij het handhaven van gegevensintegriteit en -verificatie. Door invoerinformatie om te zetten in een uitvoer van vaste grootte (of digest), zorgen hashfuncties ervoor dat geen twee verschillende invoeren dezelfde uitvoer produceren. Deze unieke eigenschap maakt het mogelijk dat de hashwaarde de originele waarde nauwkeurig identificeert.

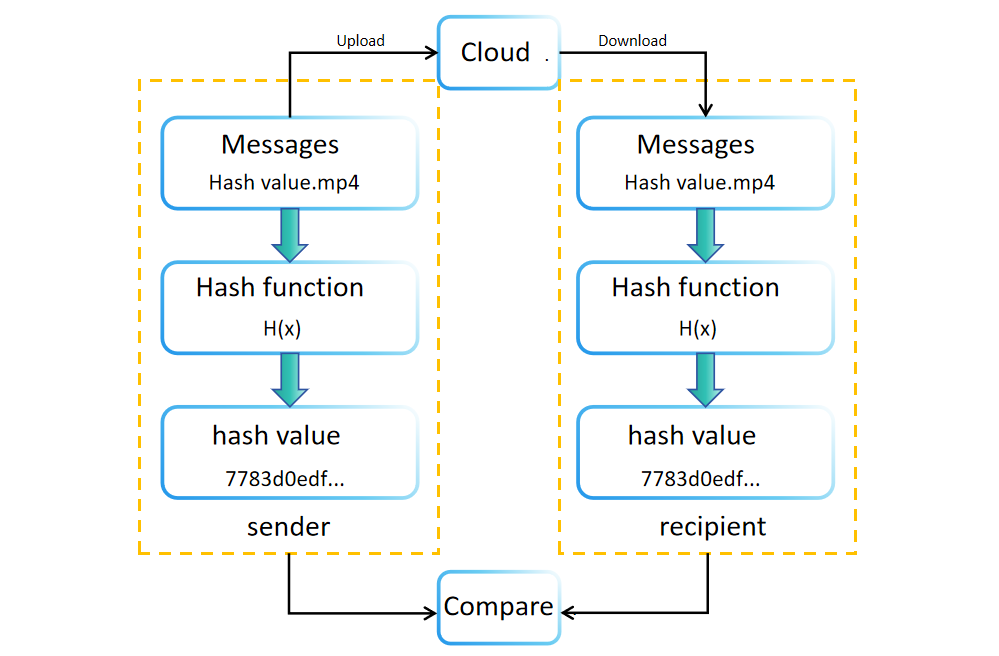
Tijdens gegevenscreatie of -opslag wordt een hashwaarde (of digest) gegenereerd met behulp van een hashfunctie. Deze waarde wordt opgeslagen of verzonden samen met de originele gegevens. Zo tonen software-downloadsites vaak bestandshashwaarden voor integriteitsverificatie. Ontvangers kunnen onafhankelijk de hashwaarde van de ontvangen gegevens opnieuw berekenen om de integriteit ervan te bevestigen. Als de originele en herberekende hashwaarden overeenkomen, is de integriteit van de gegevens geverifieerd. Zo niet, dan kunnen de gegevens zijn gemanipuleerd of beschadigd tijdens overdracht of opslag.

Het vergelijken van hashwaarden biedt ook het voordeel dat de integriteit van gegevens kan worden geverifieerd zonder dat er veel opslagruimte nodig is. Deze methode stelt ontvangers in staat de authenticiteit van gegevens te bevestigen door eenvoudig de hashwaarden voor en na de overdracht te vergelijken.

Kunnen hash botsingen worden gevonden?

Door de kenmerken van de hashfuncties die hierboven zijn genoemd, hebben we kennisgemaakt met botsingsbestendigheid. Maar is het mogelijk dat hashbotsingen bestaan, dat wil zeggen, dat twee verschillende invoeren dezelfde uitvoer produceren? Het antwoord is bevestigend, botsingen bestaan inderdaad. Volgens het duiventilprincipe, zolang de invoerruimte voldoende groot is, is er een mogelijkheid van hashbotsingen. Dit komt omdat de uitvoerruimte van hashfuncties meestal veel kleiner is dan de invoerruimte, wat onvermijdelijk leidt tot meerdere verschillende invoeren die naar dezelfde uitvoer worden gemapt.

Het duiventilprincipe is een eenvoudig en intuïtief principe van combinatorische wiskunde, dat stelt dat als er meer dan n objecten in n containers worden geplaatst, dan zal ten minste één container twee of meer objecten bevatten. Dit principe kan ook worden gebruikt om problemen zoals de verjaardagsparadox uit te leggen.

De toepassing van het duiventilprincipe is zeer breed, met belangrijke toepassingen in vakgebieden zoals cryptografie, informatica en wiskunde. Bijvoorbeeld, in de informatica wordt het duiventilprincipe gebruikt om de correctheid van bepaalde algoritmen te bewijzen of om de tijdscomplexiteit van algoritmen te analyseren. In de cryptografie wordt het duiventilprincipe ook gebruikt om bepaalde cryptografische aanvalsmethoden te ontwerpen, zoals de verjaardagsaanval.

De verjaardagsparadox is een klassieke toepassing van het duiventilprincipe. Stel dat er n mensen in een kamer zijn. Als we willen dat de kans dat ten minste twee mensen dezelfde verjaardag delen groter is dan 50%, hoeveel mensen zijn er dan nodig? Volgens het duiventilprincipe, als 367 mensen (uitgaande van 366 dagen in een jaar, plus een extra dag voor 29 februari in een schrikkeljaar) worden geplaatst in 366 "duiventillen" (d.w.z. verjaardagen), dan zal ten minste één "duiventil" twee mensen bevatten, wat betekent dat ten minste twee mensen dezelfde verjaardag delen. Dit illustreert de verjaardagsparadox.

Het is belangrijk op te merken dat, hoewel het duiventilprincipe eenvoudig en intuïtief is, de toepassing ervan rekening moet houden met de specifieke context. Bijvoorbeeld, bij het toepassen van het duiventilprincipe, is het noodzakelijk om ervoor te zorgen dat de betrokken willekeurige variabelen onafhankelijk van elkaar zijn; anders kan dit leiden tot onjuiste conclusies. Bovendien is het in sommige gevallen ook nodig om factoren zoals de grootte en vorm van de duiventillen in overweging te nemen.

Het proberen te vinden van hash botsingen door eenvoudigweg de invoerruimte te doorlopen, is echter mogelijk niet praktisch, voornamelijk om twee redenen:

• Berekeningscomplexiteit: Voor de meeste hashfuncties is de invoerruimte enorm. Neem SHA-256 als voorbeeld; de output is een 256-bit hashwaarde, wat betekent dat er 2^256 mogelijke outputs zijn. Omdat een van de ontwerpdoelen van hashfuncties is om botsingen zoveel mogelijk te minimaliseren, zou theoretisch het vinden van een hashbotsing voor SHA-256 vereisen om ongeveer 2^(256/2) = 2^128 invoeren te doorlopen, volgens de verjaardagsparadox, wat het ongeveer verwachte aantal invoeren is om een botsing te vinden. Zelfs met de krachtigste supercomputers die momenteel beschikbaar zijn, zou het ver buiten een mensenleven duren om een dergelijke taak te voltooien. waardoor het als onmogelijk wordt beschouwd om een SHA-256 hashbotsing te vinden door eenvoudige doorloop.
• Ontwerp van hashfuncties: Hashfuncties zijn typisch ontworpen om het vinden van botsingen rekenkundig onuitvoerbaar te maken. Dit betekent dat, hoewel botsingen theoretisch bestaan, ze in de praktijk praktisch onmogelijk te vinden zijn. Dit is een belangrijke kenmerk van cryptografische hashfuncties (zoals SHA-256), die veel worden gebruikt in gebieden zoals digitale handtekeningen, wachtwoordopslag, en meer.

Natuurlijk kunnen we ook specifieke algoritmes gebruiken om te proberen hashbotsingen te vinden. Deze algoritmes maken vaak gebruik van enkele bekende eigenschappen of zwakheden van hashfuncties om botsingen te vinden. Hier zijn enkele gangbare technieken en methoden voor het vinden van hashbotsingen:

• Verjaardagsaanval: Dit is een op waarschijnlijkheid gebaseerde eenvoudige methode die wordt gebruikt om de benodigde tijd in te schatten om een botsing te vinden wanneer invoeren willekeurig worden gekozen. Het principe van de verjaardagsaanval is dat als er veel mensen in een kamer zijn, de kans dat twee mensen dezelfde verjaardag hebben toeneemt met het aantal mensen. Op dezelfde manier, in hashfuncties, als een voldoende aantal invoeren willekeurig wordt geselecteerd, is het waarschijnlijk dat twee invoeren uiteindelijk dezelfde hashuitvoer produceren.
• Brute Force Aanval: Dit is de meest eenvoudige methode, die alle mogelijke invoeren doorloopt om een botsing te vinden. Deze methode is echter onpraktisch voor hashfuncties met grote invoerruimten vanwege de enorme rekenkracht en tijd die nodig zijn.
• Regenboogtabellen: Deze techniek wordt gebruikt om een groot aantal hashwaarden en hun overeenkomstige invoeren vooraf te berekenen en op te slaan. Regenboogtabellen zijn vooral nuttig voor het kraken van wachtwoorden die geen willekeurige data-obfuscatie hebben gebruikt of een bekende hashfunctie hebben. Door op te zoeken in de regenboogtabel, kan een aanvaller snel een invoer vinden die overeenkomt met een specifieke hashwaarde.
• Hash Extensie Aanvallen: Bepaalde hashfuncties laten aanvallers toe om extra gegevens te combineren met een bekende hashwaarde zonder de originele invoer te kennen, waardoor een nieuwe hashwaarde wordt gegenereerd. Deze aanval kan worden gebruikt om botsingen te construeren of andere soorten aanvallen uit te voeren.
• Speciaal Geconstrueerde Invoeren: Soms kunnen aanvallers specifieke zwakheden of niet-lineair gedrag in hashfuncties exploiteren om speciale invoeren te construeren die meer kans hebben om botsingen in de hashfunctie te produceren.

Wat zijn de meest gebruikte hashfuncties?

MD5 (Message Digest Algorithm 5)

MD5 is een veelgebruikte cryptografische hashfunctie, ontworpen door Ronald Rivest in de jaren '90 als vervanging van het oudere MD4-algoritme. Het kan een bericht van elke lengte omzetten in een vaste lengte hashwaarde (128 bits, of 16 bytes). Het ontwerpdoel van MD5 was om een snelle en relatief veilige manier te bieden om een digitale vingerafdruk van gegevens te genereren. Echter, botsingsmethoden voor MD5 zijn ontdekt, waardoor het algoritme onveilig is geworden, maar het wordt nog steeds veel gebruikt in situaties waar veiligheid geen primaire zorg is.

Het berekeningsproces van MD5 omvat de volgende stappen:

• Padding: Aanvankelijk worden de originele gegevens opgevuld zodat de byte-lengte een veelvoud is van 512. De opvulling begint met een 1, gevolgd door 0en totdat aan de lengtevereiste is voldaan.
• Lengte toevoegen: Een 64-bits lengtewaarde, die de binaire representatie van de originele berichtlengte is, wordt toegevoegd aan het opgevulde bericht, waardoor de uiteindelijke berichtlengte een veelvoud van 512 bits wordt.
• Initialiseren van de MD-buffer: Vier 32-bits registers (A, B, C, D) worden geïnitialiseerd om de tussenliggende en uiteindelijke hashwaarden op te slaan.
• Berichtblokken verwerken: Het opgevulde en lengte-verwerkte bericht wordt verdeeld in blokken van 512 bits, en elk blok wordt verwerkt door vier ronden van operatie. Elke ronde bevat 16 vergelijkbare operaties gebaseerd op niet-lineaire functies (F, G, H, I), links circulaire verschuivingsoperaties, en optelling modulo 32.
• Output: De uiteindelijke hashwaarde is de inhoud van de laatste toestand van de vier registers A, B, C, D aan elkaar gekoppeld (elk register is 32 bits), waardoor een 128-bits hashwaarde wordt gevormd.

SHA-1 (Secure Hash Algorithm 1)

SHA-1 is ontworpen door de United States National Security Agency (NSA) en uitgebracht als een Federal Information Processing Standard (FIPS PUB 180-1) door het National Institute of Standards and Technology (NIST) in 1995. SHA-1 is bedoeld voor gebruik in digitale handtekeningen en andere cryptografische toepassingen, en genereert een 160-bit (20-byte) hashwaarde, bekend als een berichtsamenvatting. Hoewel nu bekend is dat SHA-1 beveiligingskwetsbaarheden heeft en is vervangen door veiligere algoritmen zoals SHA-256 en SHA-3, het begrijpen van zijn werkingsprincipe heeft nog steeds educatieve en historische waarde.

Het ontwerpdoel van SHA-1 is om een bericht van willekeurige lengte te nemen en een 160-bit berichtsamenvatting te produceren om de integriteit van de gegevens te verifiëren. Het berekeningsproces kan worden verdeeld in de volgende stappen:

• Padding: Aanvankelijk wordt het oorspronkelijke bericht opgevuld zodat de lengte (in bits) modulo 512 gelijk is aan 448. De opvulling begint altijd met een "1" bit, gevolgd door meerdere "0" bits, totdat aan de bovenstaande lengtevoorwaarde is voldaan.
• Lengte toevoegen: Een 64-bits blok wordt toegevoegd aan het opgevulde bericht, dat de lengte van het oorspronkelijke bericht (in bits) vertegenwoordigt, waardoor de uiteindelijke berichtlengte een veelvoud van 512 bits wordt.
• Buffer initialiseren: Het SHA-1-algoritme gebruikt een 160-bits buffer, verdeeld in vijf 32-bits registers (A, B, C, D, E), om de tussenliggende en uiteindelijke hashwaarden op te slaan. Deze registers worden geïnitialiseerd naar specifieke constante waarden aan het begin van het algoritme.
• Berichtblokken verwerken: Het voorverwerkte bericht wordt verdeeld in blokken van 512 bits. Voor elk blok voert het algoritme een hoofdlus uit die 80 vergelijkbare stappen bevat. Deze 80 stappen zijn verdeeld in vier rondes, elk met 20 stappen. Elke stap gebruikt een andere niet-lineaire functie (F, G, H, I) en een constante (K). Deze functies zijn ontworpen om de complexiteit en veiligheid van de operaties te vergroten. In deze stappen gebruikt het algoritme bitgewijze operaties (zoals EN, OF, XOR, NIET) en optelling modulo 32, evenals links circulaire verschuivingen.
• Output: Na het verwerken van alle blokken worden de opgebouwde waarden in de vijf registers aan elkaar gekoppeld om de uiteindelijke 160-bit hashwaarde te vormen.

SHA-2 (Secure Hash Algorithm 2)

SHA-2 is een familie van cryptografische hashfuncties, bestaande uit verschillende versies, voornamelijk zes varianten: SHA-224, SHA-256, SHA-384, SHA-512, SHA-512/224, en SHA-512/256. SHA-2 is ontworpen door de United States National Security Agency (NSA) en gepubliceerd als een Federal Information Processing Standard (FIPS) door het National Institute of Standards and Technology (NIST). In vergelijking met zijn voorganger, SHA-1, biedt SHA-2 verbeterde beveiliging, voornamelijk weerspiegeld in langere hashwaarden en sterkere weerstand tegen botsingsaanvallen.

De werking van de SHA-2 familie lijkt in veel opzichten op SHA-1 maar biedt hogere beveiliging door het gebruik van langere hashwaarden en een complexer verwerkingsprocedure. Hier zijn de belangrijkste stappen van het SHA-2 algoritme:

• Padding: Het invoerbericht wordt eerst opgevuld om de lengte ervan, minus 64 bits, gelijk te maken aan 448 of 896 op een modulo 512 (voor SHA-224 en SHA-256) of modulo 1024 (voor SHA-384 en SHA-512) basis. De opvulmethode is hetzelfde als bij SHA-1, wat inhoudt dat een "1" aan het einde van het bericht wordt toegevoegd, gevolgd door meerdere "0"en, en uiteindelijk een 64-bits (voor SHA-224 en SHA-256) of 128-bits (voor SHA-384 en SHA-512) binaire representatie van de originele berichtlengte in bits.
• Buffer initialiseren: Het SHA-2 algoritme gebruikt een reeks geïnitialiseerde hashwaarden als startbuffer, afhankelijk van de gekozen SHA-2 variant. Bijvoorbeeld, SHA-256 gebruikt acht 32-bits registers, terwijl SHA-512 acht 64-bits registers gebruikt. Deze registers worden geïnitialiseerd met specifieke constante waarden.
• Berichtblokken verwerken: Het opgevulde bericht wordt verdeeld in 512-bits of 1024-bits blokken, en elk blok ondergaat meerdere rondes van cryptografische operaties. SHA-256 en SHA-224 voeren 64 rondes van operaties uit, terwijl SHA-512, SHA-384, SHA-512/224, en SHA-512/256 80 rondes uitvoeren. Elke ronde van operatie bevat een reeks complexe bitwise operaties, inclusief logische, modulaire toevoeging, en conditionele operaties, steunend op verschillende niet-lineaire functies en vooraf gedefinieerde constanten. Deze operaties verhogen de complexiteit en beveiliging van het algoritme.
• Output: Uiteindelijk, na het verwerken van alle blokken, worden de waarden in de buffer gecombineerd om de uiteindelijke hashwaarde te vormen. Afhankelijk van de SHA-2 variant, kan deze hashwaarde 224, 256, 384 of 512 bits lang zijn.

Je vraagt je misschien af waarom de invoer naar een hashfunctie van willekeurige lengte kan zijn, maar de uitvoer vast is. De reden is dat de SHA-2 familie de Merkle-Damgård transformatie gebruikt, die de constructie van hashfuncties mogelijk maakt die berichten van elke lengte kunnen verwerken vanuit een compressiefunctie van vaste lengte. De Merkle-Damgård transformatie wordt aangenomen in veel traditionele hashfuncties, inclusief MD5 en SHA-1.

Het kernidee van de Merkle-Damgård transformatie is om het invoerbericht te verdelen in blokken van vaste grootte en vervolgens deze blokken een voor een te verwerken, waarbij elke verwerkingsstap afhankelijk is van het resultaat van de vorige, uiteindelijk resulterend in een vaste hashwaarde. De opvulstap van SHA-256 belichaamt de basisprincipes van de Merkle-Damgård transformatie, namelijk door geschikt opvullen om berichten van elke lengte te verwerken en te zorgen dat de uiteindelijke verwerkte berichtlengte aan bepaalde voorwaarden voldoet (zoals een veelvoud zijn van een vaste lengte). Daarom kan worden gezegd dat de opvulstap van SHA-256 de Merkle-Damgård transformatiemethode volgt.

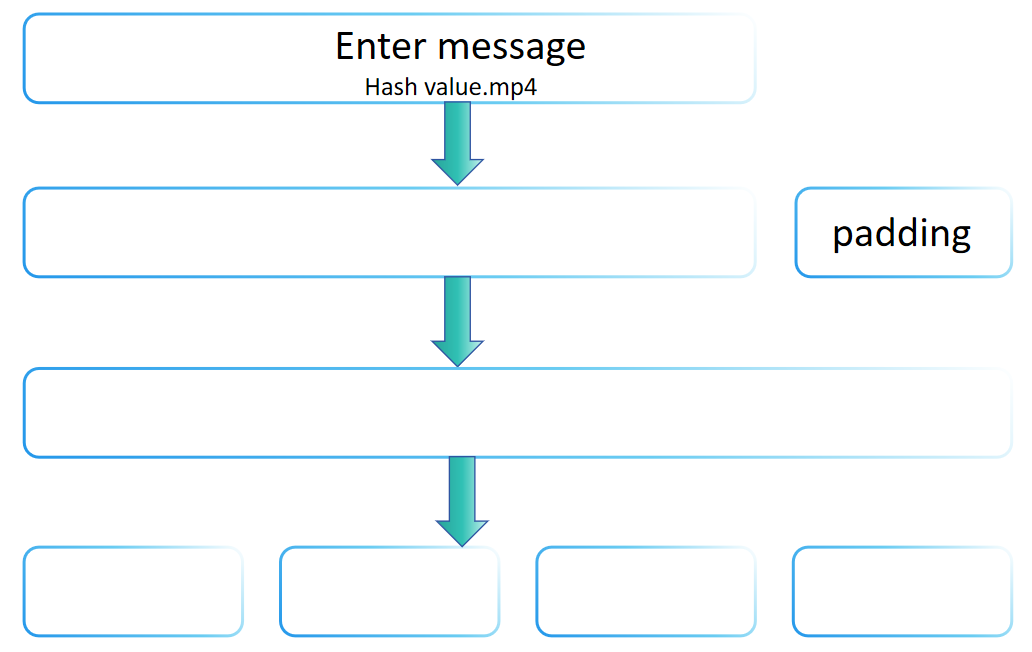
Echter, SHA-256 is niet slechts een directe implementatie van de Merkle-Damgård transformatie. Het omvat ook een reeks complexe computationele stappen (zoals berichtuitbreiding, meerdere rondes van compressiefuncties, etc.), die unieke ontwerpen van SHA-256 zijn, gericht op het verbeteren van de beveiliging. Daarom, hoewel SHA-256 de principes van de Merkle-Damgård transformatie volgt in zijn opvulstap, verhoogt het de algehele beveiliging door andere beveiligingsmechanismen te introduceren, waardoor het niet beperkt blijft tot het basisraamwerk van de Merkle-Damgård transformatie.

SHA-3 (Secure Hash Algorithm 3)

SHA-3 is de nieuwste beveiligde hash-standaard, officieel goedgekeurd door het National Institute of Standards and Technology (NIST) in 2015 als een Federal Information Processing Standard (FIPS 202). SHA-3 is niet bedoeld om de eerdere SHA-1 of SHA-2 te vervangen (aangezien SHA-2 nog steeds als veilig wordt beschouwd), maar eerder om een aanvullende en alternatieve optie binnen de SHA-familie te bieden, door een ander cryptografisch hash-algoritme aan te bieden. SHA-3 is gebaseerd op het Keccak-algoritme, ontworpen door Guido Bertoni en anderen, en was de winnaar van de SHA-3 competitie gehouden door NIST in 2012.

Het werkingsprincipe van SHA-3 verschilt aanzienlijk van SHA-2, voornamelijk omdat het een methode gebruikt die bekend staat als "sponge constructie" om gegevens te absorberen en uit te persen, waardoor de uiteindelijke hashwaarde wordt geproduceerd. Deze methode stelt SHA-3 in staat om flexibel hashwaarden van verschillende lengtes uit te voeren, waardoor het een breder scala aan toepassingen biedt dan SHA-2. De belangrijkste stappen van SHA-3 zijn als volgt:

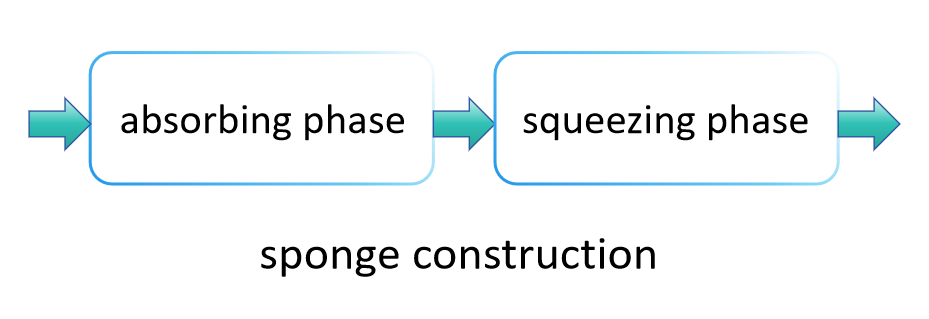
Absorptiefase:

In de absorptiefase verdeelt de sponsstructuur eerst de invoergegevens in blokken van vaste grootte. Deze datablokken worden sequentieel "geabsorbeerd" in de interne staat van de spons, die doorgaans groter is dan een enkel datablok, om ervoor te zorgen dat een grote hoeveelheid gegevens kan worden verwerkt zonder overloop. Specifiek wordt elk datablok op een bepaalde manier samengevoegd met een deel van de interne staat (zoals door een XOR-operatie), gevolgd door de toepassing van een vaste permutatiefunctie (in SHA-3, dit is Keccak-f ) om de hele staat te transformeren, daardoor interferentie tussen verschillende invoergegevensblokken voorkomend. Dit proces wordt herhaald totdat alle invoergegevensblokken zijn verwerkt.

Keccak-f is de kernpermutatiefunctie die wordt gebruikt in het SHA-3 cryptografische hashalgoritme. Het is een centraal onderdeel van de Keccak-algoritme familie. SHA-3 is gebaseerd op het Keccak-algoritme, dat de cryptografische hashalgoritme competitie gehouden door NIST won en werd geselecteerd als de standaard voor SHA-3. De Keccak-f-functie heeft verschillende varianten, waarbij de meest gebruikte Keccak-f[1600] is, waarbij het getal de bitbreedte aangeeft waarop het werkt.

Keccak-f bestaat uit meerdere rondes van dezelfde operatie (aangeduid als rondes). Voor Keccak-f[1600] zijn er in totaal 24 ronden van operaties. Elke ronde omvat vijf basisstappen: θ (Theta), ρ (Rho), π (Pi), χ (Chi), en ι (Iota). Deze stappen werken samen aan de staat array, waardoor de inhoud geleidelijk wordt getransformeerd, verwarring en verspreiding toenemend om de beveiliging te verbeteren. Hieronder volgt een korte beschrijving van deze stappen:

• θ (Theta) stap: Voert XOR-operaties uit op alle bits van elke kolom, vervolgens XORs het resultaat op aangrenzende kolommen, waardoor diffusie tussen kolommen ontstaat.
• ρ (Rho) stap: Bit-niveau rotatieoperatie, waarbij elke bit een ander aantal bits wordt gedraaid volgens vooraf bepaalde regels, waardoor de complexiteit van de gegevens toeneemt.
• π (Pi) stap: Herschikt de bits in de staat array, waardoor de positie van de bits wordt gewijzigd om diffusie over rijen en kolommen te bereiken.
• χ (Chi) stap: Een niet-lineaire stap die XOR-operaties uitvoert op elke bit van elke rij, inclusief zichzelf, zijn onmiddellijke buurman, en het complement van de buurman. Dit is een lokale operatie die de niet-lineaire kenmerken van het cryptografische algoritme verhoogt.
• ι (Iota) stap: Voegt een ronde constante toe aan een deel van de staat array, met de constante die in elke ronde verschilt, om te voorkomen dat alle rondes identiek werken, onvoorspelbaarheid introducerend.

Keccak-f biedt een hoog niveau van beveiliging door deze stappen. Het ontwerp zorgt ervoor dat zelfs kleine veranderingen in de invoer leiden tot wijdverspreide en onvoorspelbare veranderingen in de staat array, bereikt door de principes van verwarring (het moeilijk maken voor aanvallers om de invoer uit de uitvoer af te leiden) en verspreiding (waar kleine veranderingen in de invoer meerdere delen van de uitvoer beïnvloeden).

Het ontwerp van Keccak-f staat aanpassing van parameters toe (zoals staatgrootte en aantal rondes) over verschillende beveiligingsniveaus en toepassingsscenario's, wat grote flexibiliteit biedt. Keccak-f[1600] staat bekend om zijn efficiënte implementatie, die hoge verwerkingssnelheden bereikt, zowel in hardware als in software, vooral bij het verwerken van grote hoeveelheden gegevens.

Uitknijpfase:

Zodra alle invoergegevensblokken in de interne staat zijn geabsorbeerd, gaat de sponsstructuur over naar de uitknijpfase. In deze fase worden delen van de interne staat geleidelijk uitgevoerd als het resultaat van de hashfunctie. Als de vereiste uitvoerlengte groter is dan wat in één keer kan worden uitgeknepen, past de sponsstructuur de permutatiefunctie toe om de interne staat opnieuw te transformeren en vervolgens meer gegevens uit te voeren. Dit proces wordt voortgezet totdat de gewenste uitvoerlengte is bereikt.

Het doel van het ontwerp van SHA-3 is om een hogere beveiliging dan SHA-2 te bieden en betere weerstand tegen aanvallen van kwantumcomputing. Dankzij zijn unieke sponsstructuur is SHA-3 in theorie in staat om alle momenteel bekende cryptografische aanvalsmethoden te weerstaan, inclusief botsingsaanvallen, preimage-aanvallen en second preimage-aanvallen.

RIPEMD-160 (RACE Integrity Primitives Evaluation Message Digest)

RIPEMD-160 is een cryptografische hashfunctie ontworpen om een veilig hashalgoritme te bieden. Het werd in 1996 ontwikkeld door Hans Dobbertin en anderen en maakt deel uit van de RIPEMD (RACE Integrity Primitives Evaluation Message Digest) familie.

RIPEMD-160 produceert een 160-bit (20-byte) hashwaarde, wat de oorsprong is van de "160" in zijn naam. Het is gebaseerd op het ontwerp van MD4 en beïnvloed door andere hashalgoritmes zoals MD5 en SHA-1. RIPEMD-160 omvat twee parallelle, vergelijkbare bewerkingen die de invoergegevens afzonderlijk verwerken en vervolgens de resultaten van deze twee processen combineren om de uiteindelijke hashwaarde te genereren. Dit ontwerp heeft als doel de beveiliging te verbeteren.

Het berekeningsproces van RIPEMD-160 omvat verschillende basisstappen: padding, blokverwerking en compressie:

• Padding: Het invoerbericht wordt eerst aangevuld om ervoor te zorgen dat de lengte modulo 512 bits gelijk is aan 448 bits. De padding begint altijd met een enkele bit van 1, gevolgd door een reeks van 0 bits, eindigend met een 64-bits representatie van de oorspronkelijke berichtlengte.
• Blokverwerking: Het aangevulde bericht wordt verdeeld in 512-bit blokken.
• Initialisatie: Er worden vijf 32-bit registers (A, B, C, D, E) gebruikt, die geïnitialiseerd zijn op bepaalde specifieke waarden.
• Compressiefunctie: Elk blok wordt achtereenvolgens verwerkt, waarbij de waarden van deze vijf registers worden bijgewerkt door een reeks complexe bewerkingen. Dit proces omvat bitgewijze bewerkingen (zoals optellen, EN, OF, NIET, circulaire linksverschuivingen) en het gebruik van een reeks vaste constanten.
• Uitvoer: Nadat alle blokken zijn verwerkt, worden de waarden van deze vijf registers samengevoegd om de uiteindelijke 160-bit hashwaarde te vormen.