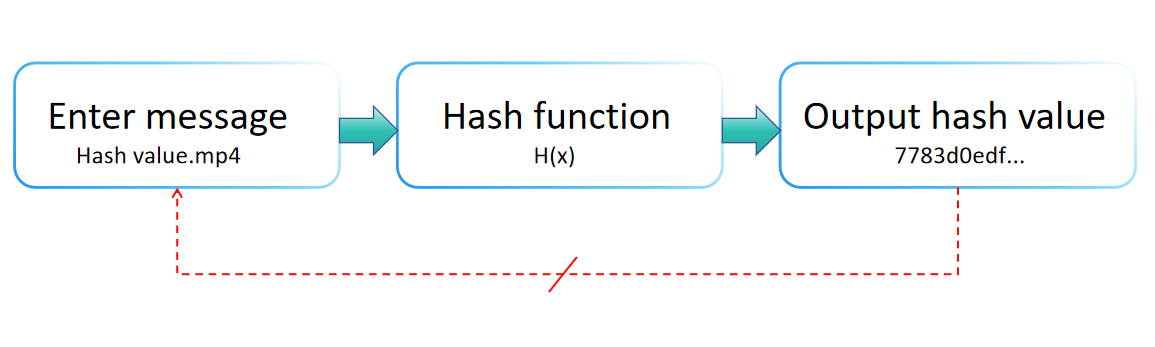
اختبار قيمة الهاش
أدخل نصًا لعرض عملية تحويله إلى قيمة هاش في الوقت الفعلي،
أو اختر ملفًا لحساب قيمة هاش الملف.
إنشاء قيمة هاش للنص
مقارنة قيمة هاش النص
إنشاء قيمة هاش للملف
مقارنة قيمة هاش الملف
قيمة تجزئة الإدخال 1
قيمة تجزئة الإدخال 2
"في عصرنا الرقمي الحالي، لا تعتبر أمان البيانات فقط حجر الزاوية لحماية الخصوصية الشخصية وأسرار الشركات، ولكنها أيضًا المفتاح للحفاظ على الثقة الاجتماعية والاستقرار الاقتصادي."
ما هي قيمة الهاش؟
قيمة الهاش هي سلسلة أو رقم ذو حجم ثابت يتم إنشاؤه من أي حجم للبيانات الإدخالية بواسطة دالة الهاش. تقبل هذه الوظائف مدخلات متنوعة مثل النصوص، الصور، والفيديوهات، مُنتجة قيمة هاش ثابتة الطول ولا رجعة فيها. قيم الهاش حتمية، مما يعني أن المدخلات المتطابقة تؤدي دائمًا إلى نفس الناتج. كما أنها تتميز بمقاومة التصادم، مما يجعل من الصعب العثور على مدخلات مختلفة تؤدي إلى نفس الناتج.
وظائف قيمة الهاش
تؤدي قيم الهاش أدوارًا أساسية في علوم الحاسوب وتكنولوجيا المعلومات، مقدمة ملخصًا ثابت الطول للبيانات بغض النظر عن حجمها. تسهل هذه الوظائف تطبيقات متعددة:
- التحقق من سلامة البيانات: تُستخدم للتحقق مما إذا كانت البيانات ظلت دون تعديل أثناء النقل، مضمونةً سلامة الملفات المحملة.
- تخزين كلمات المرور: تُخزن كلمات المرور كقيم هاش للأمان، مما يجعل من الصعب استرداد كلمات المرور الأصلية من قواعد البيانات المخترقة.
- استرجاع البيانات بسرعة: تعمل قيم الهاش كمؤشرات في جداول الهاش، مما يسمح بتنفيذ عمليات البيانات بكفاءة.
- إزالة التكرارات في البيانات: تساعد في تحديد وإزالة العناصر المكررة للبيانات عن طريق مقارنة قيم الهاش.
- التوقيع الرقمي والتحقق منه: يضمن سلامة البيانات ومصدرها من خلال التشفير العام ووظائف الهاش.
- تكنولوجيا البلوكتشين: تستخدم قيم الهاش لتأمين سجلات المعاملات وضمان عدم قابلية البيانات للتغيير.
- طوابع زمنية مضادة للتلاعب: توفر طابعًا زمنيًا لا رجعة فيه للبيانات، مفيد في حماية حقوق الطبع والنشر والحماية القانونية.
السبب في فعالية قيم الهاش في هذه المجالات يعود إلى خصائصها الأساسية المتمثلة في السرعة، الحتمية، عدم القابلية للعكس، ومقاومة التصادم. عند استخدامها بشكل صحيح، يمكن أن توفر وظائف الهاش دعمًا قويًا في تأمين البيانات، تعزيز الكفاءة، والتحقق من صحة المعلومات.
ما هي دالة الهاش؟
دالة الهاش هي بنية رياضية تربط بيانات الإدخال (أو "الرسالة") بسلسلة ذات حجم ثابت، عادةً قيمة عددية، كما هو موضح في الرسم البياني أدناه. تُستخدم على نطاق واسع في إدارة البيانات وأمن المعلومات، وتتميز دالة الهاش بأدائها الحسابي الفعال، طول الإخراج المتسق، عدم القابلية للعكس، الحساسية لتغيرات الإدخال، ومقاومة التصادم.

الأداء الحسابي الفعال
يمكن لدوال الهاش حساب قيم الهاش بسرعة من بيانات أي شكل، بغض النظر عن حجم البيانات. هذه الخاصية حاسمة للتطبيقات التي تتطلب وصولاً سريعًا إلى البيانات، مثل جداول الهاش. وذلك لأنه، عند تخزين البيانات في جداول الهاش، فإن سرعة دالة الهاش تحدد سرعة استرجاع البيانات. تستخدم جداول الهاش دوال الهاش لتحديد موقع تخزين البيانات بسرعة، معتمدة على القدرة الحسابية السريعة لدوال الهاش.
علاوة على ذلك، في الأنظمة التي تحتاج إلى معالجة كميات كبيرة من البيانات، تؤثر كفاءة دوال الهاش بشكل مباشر على أداء النظام العام. إذا كانت دالة الهاش تعمل ببطء، فإنها ستصبح عائقًا في أداء النظام. بعض الأنظمة الوقتية الفعلية، مثل تصفية الحزم في أجهزة الشبكة، تتطلب حساب قيم الهاش فورًا للبيانات لاتخاذ قرارات سريعة. في هذه الحالات، تكون كفاءة دوال الهاش مهمة بنفس القدر.
على سبيل المثال، ضع في اعتبارك منصة تجارة إلكترونية عبر الإنترنت حيث قد يدخل المستخدمون أسماء المنتجات في شريط البحث للعثور على المنتجات. قد يستخدم النظام الخلفي دوال الهاش لتحديد موقع معلومات المنتج المخزنة في جداول الهاش بسرعة. إذا كانت عملية حساب دالة الهاش بطيئة، فسيتأثر تجربة المستخدم بشكل كبير، حيث سيتعين عليهم الانتظار لفترة أطول للحصول على نتائج البحث. في هذا الموقف، يضمن الأداء الحسابي الفعال لدوال الهاش أوقات استجابة سريعة، مما يحسن تجربة المستخدم. [اعرف أكثر]
ثبات طول الإخراج في دوال الهاش
تحول دوال الهاش الإدخال بأي طول إلى إخراج ذو طول ثابت من خلال سلسلة معقدة من العمليات الحسابية. غالبًا ما يتضمن هذا العملية تقسيم بيانات الإدخال إلى كتل ذات حجم ثابت (لتلك المدخلات التي تتجاوز حجم وحدة المعالجة)، تطبيق سلسلة من العمليات الحسابية والمنطقية على كل كتلة، ثم دمج أو تراكم نتائج هذه العمليات بطريقة ما لإنتاج قيمة هاش ذات حجم ثابت في النهاية.
لماذا هذا مهم؟ يساعد ثبات طول الإخراج على ضمان أمان دوال الهاش. إذا كان من الممكن أن يتغير طول إخراج الهاش، فقد يكشف ذلك عن معلومات حول حجم البيانات الأصلية، والتي يمكن استغلالها بطرق معينة لمهاجمة النظام. علاوة على ذلك، يجعل طول الإخراج الثابت من الصعب على المهاجمين استنتاج خصائص بيانات الإدخال من خلال تحليل طول الإخراج. في الوقت نفسه، يبسط الإخراج ذو الطول الثابت تخزين ومقارنة قيم الهاش. يمكن لمصممي النظام معرفة مسبقًا كمية المساحة التي ستشغلها كل قيمة هاش، وهو أمر مهم جدًا لسيناريوهات مثل تصميم قواعد البيانات والنقل الشبكي. علاوة على ذلك، يصبح ثبات طول الإخراج فعالًا جدًا لمقارنة ما إذا كانت قيم الهاش متساوية لأنه يتطلب فقط مقارنة بيانات ذات طول ثابت. هذا مهم بشكل خاص عند استخدام جداول الهاش لاسترجاع البيانات بسرعة.
باعتبار SHA-256 مثالًا، تنتج هذه الدالة الهاش العملياتية التي تستخدم على نطاق واسع قيمة هاش ذات 256 بت (أي 32 بايت) دائمًا، بغض النظر عما إذا كانت بيانات الإدخال عبارة عن بايت واحد أو عدة ملايين من البايتات. يضمن هذا الثبات أن قيم هاش SHA-256 يمكن استخدامها لتطبيقات الأمان المتنوعة، مثل التوقيعات الرقمية ورموز التوثيق (MACs)، مع تبسيط سير العمل في معالجة وتخزين البيانات.
لا رجعية دوال الهاش
دوال الهاش أحادية الاتجاه، مما يعني أنه من المستحيل استنتاج البيانات الأصلية من قيمة الهاش. هذه الخاصية مهمة بشكل خاص عند تخزين كلمات المرور، حيث حتى لو تم اختراق قاعدة البيانات، لا يمكن للمهاجمين استرداد كلمات المرور من قيم الهاش. تستند لا رجعية دوال الهاش أساسًا إلى المبادئ والخصائص التالية:
- الضغط: يمكن لدوال الهاش تعيين المدخلات بأي طول (والتي قد تكون كبيرة جدًا في الاستخدام العملي) إلى إخراج ذو طول ثابت. هذا يعني أن هناك عددًا لا نهائيًا من المدخلات الممكنة المعينة إلى عدد محدود من النواتج. نظرًا لأن مساحة الإخراج (قيم الهاش) أصغر بكثير من مساحة الإدخال، فإن مدخلات مختلفة ستنتج بالضرورة عن نفس الإخراج، وهو ظاهرة تُعرف باسم "التصادم". بسبب هذا الضغط، من المستحيل تحديد المدخلات المحددة من إخراج معين (قيمة الهاش).
- عدم الخطية العالية والتعقيد: صممت دوال الهاش باستخدام عمليات حسابية ومنطقية معقدة (مثل العمليات البتية، عمليات المودولو، إلخ)، لضمان أن يكون الإخراج حساسًا للغاية للإدخال. حتى التغييرات الطفيفة في الإدخال (على سبيل المثال، تغيير بت واحد) يمكن أن تسبب تغييرات كبيرة وغير متوقعة في الإخراج (قيمة الهاش). يجعل هذا الدرجة العالية من عدم الخطية وعشوائية الإخراج من الصعب للغاية استنتاج الإدخال الأصلي من قيمة الهاش.
- أحادية الاتجاه: يضمن تصميم دوال الهاش أن عمليتها أحادية الاتجاه؛ أي أن حساب قيمة الهاش سهل، ولكن العملية العكسية (استرداد البيانات الأصلية من قيمة الهاش) غير ممكنة. هذا لأن عملية حساب دوال الهاش تتضمن سلسلة من العمليات اللا رجعية (مثل لا رجعية عمليات المودولو)، مما يضمن أنه حتى مع قيمة الهاش، من المستحيل عكس هندسة البيانات الأصلية.
- التعيين العشوائي: يجب أن تعمل دالة الهاش المثالية كـ "معين عشوائي"، بمعنى أن كل مدخل ممكن يحتمل بنفس القدر أن يُعين إلى أي نقطة في مساحة الإخراج. تضمن هذه الخاصية عدم وجود طريقة عملية للتنبؤ بالإخراج الذي سيتم تعيين مدخل معين إليه، مما يعزز لا رجعية دالة الهاش.
- الأساس الرياضي: من الناحية الرياضية، يمكن فهم لا رجعية دوال الهاش من خلال اعتمادها على "مشكلات اللوغاريتمات الختامية"، "مشكلات تحليل الأعداد الكبيرة"، أو مشكلات نظرية الأعداد الأخرى التي يصعب حلها بالقدرات الحسابية والرياضية الحالية. على سبيل المثال، قد يعتمد تصميم بعض خوارزميات الهاش بشكل غير مباشر على صعوبة حسابية لهذه المشكلات، مما يضمن لا رجعيتها.
الحساسية للإدخال وتأثير الانهيار
في تصميم دوال الهاش، تُستخدم العمليات الحسابية والمنطقية المعقدة (مثل العمليات البتية، عمليات المودولو، إلخ) لضمان أن يكون الإخراج حساسًا جدًا للإدخال. حتى التغييرات الطفيفة في الإدخال (على سبيل المثال، تغيير بت واحد) ستؤدي إلى تغييرات كبيرة وغير متوقعة في الإخراج (قيمة الهاش)، وهو ظاهرة تُعرف بـ "تأثير الانهيار". [اقرأ المزيد]
مقاومة التصادم في التشفير
مقاومة التصادم لدالة الهاش هي مفهوم حاسم في التشفير، يشير إلى مستوى أمان دالة الهاش ضد هجمات التصادم. تشير هذه الخاصية إلى أنه بالنسبة لأي دالة هاش H، من المستحيل حسابيًا العثور على مدخلين متميزين x و y (x ≠ y) بحيث H(x) = H(y). دالة الهاش ذات مقاومة التصادم القوية تجعل من الصعب للغاية العثور على مدخلين مختلفين يؤديان إلى نفس قيمة الإخراج.
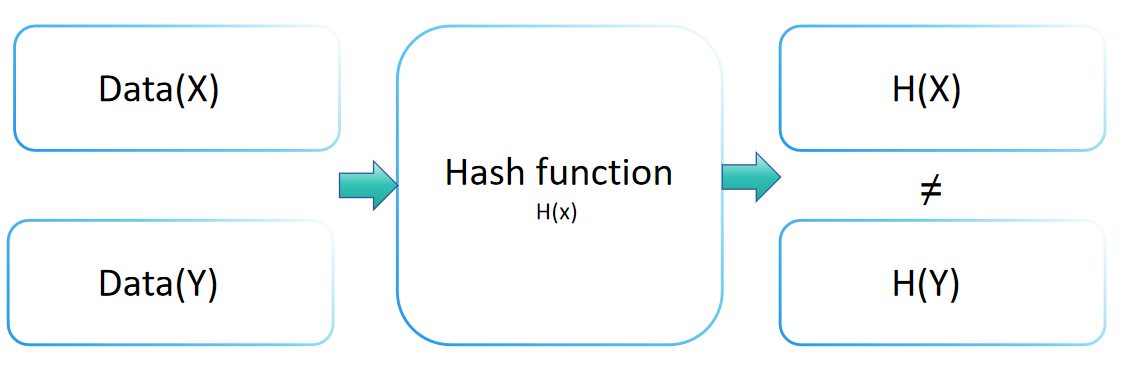
تلعب مقاومة التصادم دورًا حيويًا في الحفاظ على سلامة البيانات والتحقق منها. من خلال تحويل المعلومات المدخلة إلى إخراج ذو حجم ثابت (أو ملخص)، تضمن دوال الهاش ألا ينتج عن مدخلين مختلفين نفس الإخراج. تسمح هذه الخاصية الفريدة لقيمة الهاش بتحديد القيمة الأصلية بدقة.
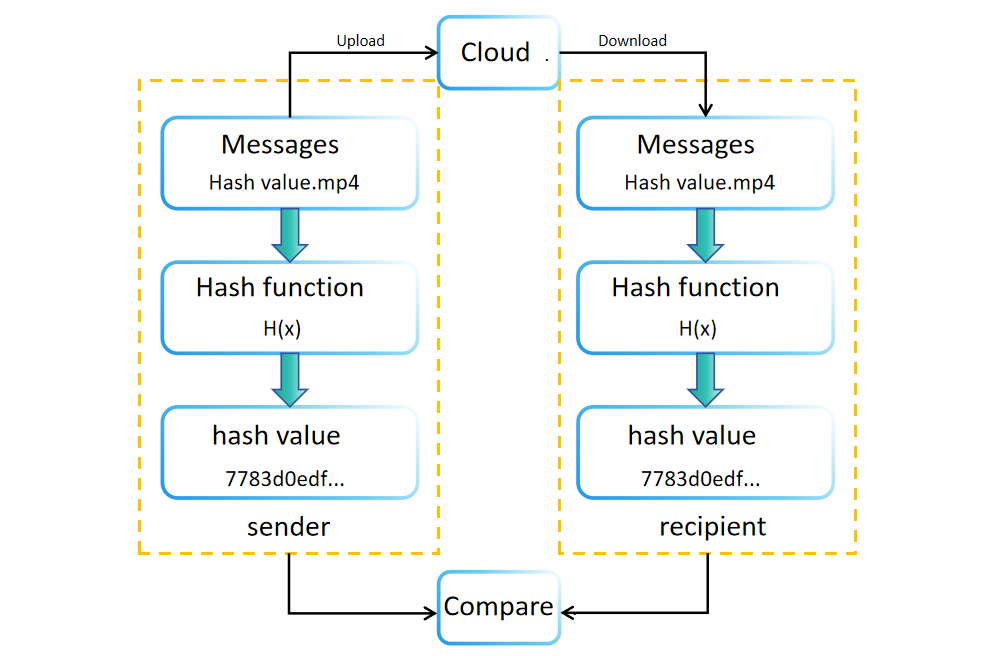
أثناء إنشاء البيانات أو تخزينها، يتم إنشاء قيمة هاش (أو ملخص) باستخدام دالة الهاش. يتم تخزين هذه القيمة أو نقلها جنبًا إلى جنب مع البيانات الأصلية. على سبيل المثال، غالبًا ما تعرض مواقع تنزيل البرامج قيم الهاش للملفات للتحقق من سلامتها. يمكن للمستلمين إعادة حساب قيمة الهاش للبيانات المستلمة بشكل مستقل للتأكد من سلامتها. إذا تطابقت قيمة الهاش الأصلية والمعاد حسابها، يتم التحقق من سلامة البيانات. إذا لم يكن الأمر كذلك، فقد تم التلاعب بالبيانات أو تلفها أثناء النقل أو التخزين.
توفر مقارنة قيم الهاش أيضًا ميزة التحقق من سلامة البيانات دون الحاجة إلى مساحة تخزين كبيرة. تتيح هذه الطريقة للمستلمين تأكيد صحة البيانات من خلال مقارنة قيم الهاش قبل وبعد النقل.
هل يمكن العثور على تصادمات الهاش؟
من خلال خصائص دوال الهاش المذكورة أعلاه، قد فهمنا مقاومة التصادم. لكن، هل من الممكن أن توجد تصادمات الهاش، أي أن ينتج عن مدخلين مختلفين نفس الناتج؟ الجواب هو نعم، توجد بالفعل تصادمات. وفقًا لـمبدأ الحفر، طالما أن فضاء الإدخال كبير بما فيه الكفاية، توجد إمكانية لتصادمات الهاش. هذا لأن فضاء الإخراج لدوال الهاش عادة ما يكون أصغر بكثير من فضاء الإدخال، مما يؤدي حتمًا إلى تعيين مدخلات مختلفة متعددة على نفس الناتج.
مبدأ الحفر هو مبدأ بديهي وبسيط من الرياضيات التوفيقية، ينص على أنه إذا تم وضع أكثر من n عناصر في n حاويات، فإن هناك حاوية واحدة على الأقل ستحتوي على عنصرين أو أكثر. يمكن استخدام هذا المبدأ أيضًا لشرح مشاكل مثل مفارقة عيد الميلاد.
تطبيق مبدأ الحفر واسع جدًا، مع استخدامات مهمة في مجالات مثل التشفير، علوم الحاسوب، والرياضيات. على سبيل المثال، في علوم الحاسوب، يُستخدم مبدأ الحفر لإثبات صحة بعض الخوارزميات أو لتحليل تعقيد الوقت للخوارزميات. في التشفير، يُستخدم مبدأ الحفر أيضًا لتصميم بعض طرق الهجوم العملياتية، مثل هجوم عيد الميلاد.
مفارقة عيد الميلاد هي تطبيق كلاسيكي لمبدأ الحفر. فلنفترض أن هناك n أشخاص في غرفة. إذا أردنا احتمالية أن يكون هناك شخصان على الأقل يشتركان في نفس تاريخ الميلاد أكبر من 50%، كم عدد الأشخاص المطلوبين؟ وفقًا لمبدأ الحفر، إذا تم وضع 367 شخصًا (بافتراض أن هناك 366 يومًا في السنة، بالإضافة إلى يوم إضافي لـ29 فبراير في سنة كبيسة) في 366 "حفرة" (أي، أعياد الميلاد)، فسيحتوي حفرة واحدة على الأقل على شخصين، مما يعني أن هناك شخصين على الأقل يشتركان في نفس تاريخ الميلاد. هذا يوضح مفارقة عيد الميلاد.
من المهم ملاحظة أنه، على الرغم من أن مبدأ الحفر بسيط وبديهي، يجب أن تأخذ تطبيقاته في الاعتبار السياق المحدد. على سبيل المثال، عند تطبيق مبدأ الحفر، من الضروري ضمان استقلالية المتغيرات العشوائية المعنية عن بعضها البعض؛ وإلا فقد يؤدي ذلك إلى استنتاجات غير صحيحة. علاوة على ذلك، في بعض الحالات، قد يكون من الضروري أيضًا مراعاة عوامل مثل حجم وشكل الحفر.
ومع ذلك، قد لا يكون محاولة العثور على تصادمات الهاش عن طريق مجرد تصفح فضاء الإدخال عمليًا، وذلك بشكل رئيسي لسببين:
- التعقيد الحسابي: بالنسبة لمعظم دوال الهاش، فإن فضاء الإدخال واسع. خذ SHA-256 كمثال؛ إخراجه هو قيمة هاش بطول 256 بت، مما يعني أن لديه 2^256 إمكانية للنواتج. نظرًا لأن أحد أهداف تصميم دوال الهاش هو تقليل التصادمات قدر الإمكان، من الناحية النظرية، من المتوقع أن يتطلب العثور على تصادم هاش لـ SHA-256 تصفح حوالي 2^(256/2) = 2^128 من المدخلات، وفقًا لمفارقة عيد الميلاد، والتي تمثل عدد المدخلات المتوقع تقريبًا لإيجاد تصادم. حتى مع أقوى الحواسيب الفائقة المتاحة حاليًا، ستستغرق هذه المهمة وقتًا يتجاوز عمر الإنسان بكثير، مما يجعل من المستحيل العثور على تصادم هاش SHA-256 من خلال التصفح البسيط.
- تصميم دوال الهاش: عادة ما تكون دوال الهاش مصممة لجعل العثور على التصادمات غير عملي حسابيًا. هذا يعني أنه، على الرغم من وجود التصادمات من الناحية النظرية، فمن المستحيل عمليًا العثور عليها في الممارسة العملية. هذه خاصية مهمة لدوال الهاش العملياتية (مثل SHA-256)، المستخدمة على نطاق واسع في مجالات مثل التوقيعات الرقمية، تخزين كلمات المرور، والمزيد.
بالطبع، يمكننا أيضًا استخدام خوارزميات محددة لمحاولة العثور على تصادمات الهاش. تستغل هذه الخوارزميات غالبًا بعض الخصائص المعروفة أو نقاط الضعف في دوال الهاش لإيجاد التصادمات. إليك بعض التقنيات والأساليب الشائعة للعثور على تصادمات الهاش:
- هجوم عيد الميلاد: هذه طريقة بسيطة مبنية على الاحتمالات تُستخدم لتقدير الوقت المطلوب لإيجاد تصادم عندما يتم اختيار المدخلات بشكل عشوائي. مبدأ هجوم عيد الميلاد هو أنه إذا كان هناك العديد من الأشخاص في غرفة، تزداد احتمالية أن يكون لدى شخصين نفس تاريخ الميلاد مع زيادة عدد الأشخاص. بشكل مماثل، في دوال الهاش، إذا تم اختيار عدد كافٍ من المدخلات بشكل عشوائي، من المحتمل أن ينتج في النهاية مدخلان نفس ناتج الهاش.
- هجوم القوة الغاشمة: هذه هي الطريقة الأكثر مباشرة، والتي تتضمن تصفح جميع المدخلات المحتملة للعثور على تصادم. ومع ذلك، هذه الطريقة غير عملية بالنسبة لدوال الهاش التي لها فضاءات إدخال كبيرة بسبب الموارد الحسابية الهائلة والوقت المطلوب.
- جداول الألوان الطيفية: تُستخدم هذه التقنية للحساب المُسبق وتخزين عدد كبير من قيم الهاش والمُدخلات المُقابلة لها. تُعد جداول الألوان الطيفية مفيدة بشكل خاص لاختراق كلمات المرور التي لم تُستخدم فيها عملية التشويش على البيانات العشوائية أو تلك التي لها دالة هاش معروفة. من خلال البحث في جدول الألوان الطيفية، يُمكن للمهاجم أن يجد بسرعة مُدخل يُطابق قيمة هاش محددة.
- هجمات تمديد الهاش: تسمح بعض دوال الهاش للمهاجمين بدمج بيانات إضافية مع قيمة هاش معروفة دون معرفة الإدخال الأصلي، مما يولد قيمة هاش جديدة. يمكن استخدام هذا الهجوم لبناء التصادمات أو تنفيذ أنواع أخرى من الهجمات.
- المدخلات المصممة خصيصًا: أحيانًا، يمكن للمهاجمين استغلال نقاط الضعف المحددة أو السلوكيات غير الخطية في دوال الهاش لبناء مدخلات خاصة من المرجح أن تنتج تصادمات في دالة الهاش.
ما هي دوال الهاش المستخدمة بشكل شائع؟
MD5 (خوارزمية الرسالة الهضمية 5)
MD5 هي دالة هاش عملياتية تستخدم على نطاق واسع، صممها رونالد ريفيست في التسعينيات لاستبدال خوارزمية MD4 الأقدم. يمكنها تحويل رسالة بأي طول إلى قيمة هاش ذات طول ثابت (128 بت أو 16 بايت).
كان الهدف من تصميم MD5 هو توفير طريقة سريعة وآمنة نسبيًا لإنشاء بصمة رقمية للبيانات. ومع ذلك، تم اكتشاف طرق التصادم لـ MD5 ، مما جعل الخوارزمية غير آمنة، لكنها لا تزال تستخدم على نطاق واسع في الحالات التي لا تكون فيها الأمان هي الشاغل الرئيسي.
تتضمن عملية حساب MD5 الخطوات التالية:
- التعبئة: في البداية، يتم تعبئة البيانات الأصلية بحيث يكون طولها بالبايت مضاعفًا لـ512. تبدأ التعبئة بـ1، يليها أصفار حتى يتم تلبية متطلبات الطول.
- إضافة الطول: يتم إضافة قيمة طول 64 بت، وهي التمثيل الثنائي لطول الرسالة الأصلية، إلى الرسالة المعبأة، مما يجعل الرسالة النهائية بطول مضاعف لـ512 بت.
- تهيئة الذاكرة الوسيطة MD: يتم تهيئة أربعة سجلات 32 بت (A، B، C، D) لتخزين قيم الهاش المتوسطة والنهائية.
- معالجة كتل الرسائل: يتم تقسيم الرسالة المعبأة والتي تمت معالجتها طولياً إلى كتل 512 بت، ويتم معالجة كل كتلة من خلال أربع جولات من العمليات. تشمل كل جولة 16 عملية مماثلة تعتمد على وظائف غير خطية (F، G، H، I)، عمليات الإزاحة الدائرية اليسرى، والجمع وفق نمط 32.
- الناتج: قيمة الهاش النهائية هي محتوى الحالة الأخيرة للسجلات الأربعة A، B، C، D المتصلة معًا (كل سجل هو 32 بت)، لتشكيل قيمة هاش بطول 128 بت.
SHA-1 (خوارزمية الهاش الآمنة 1)
تم تصميم SHA-1 بواسطة وكالة الأمن القومي الأمريكية (NSA) وأصدرت كمعيار معالجة المعلومات الاتحادي (FIPS PUB 180-1) بواسطة المعهد الوطني للمعايير والتكنولوجيا (NIST) في عام 1995.
صُمم SHA-1 للاستخدام في التوقيعات الرقمية وتطبيقات التشفير الأخرى، مولدًا قيمة هاش بطول 160 بت (20 بايت) تُعرف بموجز الرسالة. على الرغم من أنه أصبح معروفًا الآن أن SHA-1 له نقاط ضعف أمنية وقد تم استبداله بخوارزميات أكثر أمانًا مثل SHA-256 وSHA-3،
فإن فهم مبدأ عمله لا يزال يحمل قيمة تعليمية وتاريخية.
الغرض من تصميم SHA-1 هو أخذ رسالة بطول عشوائي وإنتاج موجز رسالة بطول 160 بت للتحقق من سلامة البيانات. يمكن تقسيم عملية حسابها إلى الخطوات التالية:
- التعبئة: في البداية، يتم تعبئة الرسالة الأصلية بحيث يكون طولها (بالبتات) مضاعفًا لـ512 يساوي 448. التعبئة تبدأ دائمًا ببت "1"، يليها عدة بتات "0"، حتى يتم تلبية شرط الطول المذكور.
- إضافة الطول: يتم إضافة كتلة 64 بت إلى الرسالة المعبأة، تمثل طول الرسالة الأصلية (بالبتات)، مما يجعل طول الرسالة النهائي مضاعفًا لـ512 بت.
- تهيئة الذاكرة الوسيطة: يستخدم خوارزم SHA-1 ذاكرة وسيطة بطول 160 بت، مقسمة إلى خمسة سجلات 32 بت (A، B، C، D، E)، لتخزين قيم الهاش المتوسطة والنهائية. يتم تهيئة هذه السجلات إلى قيم ثابتة محددة في بداية الخوارزمية.
- معالجة كتل الرسائل: يتم تقسيم الرسالة المعالجة مسبقًا إلى كتل بطول 512 بت. لكل كتلة، ينفذ الخوارزم الحلقة الرئيسية التي تحتوي على 80 خطوة مماثلة. تنقسم هذه الـ80 خطوة إلى أربع جولات، كل منها به 20 خطوة. تستخدم كل خطوة وظيفة غير خطية مختلفة (F، G، H، I) وثابت (K). تم تصميم هذه الوظائف لزيادة تعقيد وأمان العمليات. في هذه الخطوات، يستخدم الخوارزم العمليات البتية (مثل AND، OR، XOR، NOT) والجمع وفق نمط 32، بالإضافة إلى الإزاحات الدائرية اليسرى.
- الناتج: بعد معالجة جميع الكتل، يتم دمج القيم المتراكمة في السجلات الخمسة لتشكيل القيمة النهائية للهاش بطول 160 بت.
SHA-2 (خوارزمية الهاش الآمنة 2)
SHA-2 هي عائلة من دوال الهاش العملياتية، تشمل عدة نسخ مختلفة، تتكون أساسًا من ستة متغيرات: SHA-224، SHA-256، SHA-384، SHA-512، SHA-512/224، و SHA-512/256.
تم تصميم SHA-2 بواسطة وكالة الأمن القومي الأمريكية (NSA) ونشرت كمعيار معالجة المعلومات الفيدرالي (FIPS) بواسطة المعهد الوطني للمعايير والتكنولوجيا (NIST). مقارنةً بسلفها SHA-1، تقدم SHA-2 أمانًا محسنًا، ينعكس بشكل أساسي في قيم الهاش الأطول ومقاومة أقوى لهجمات التصادم.
تشابه عملية عائلة SHA-2 مع SHA-1 في العديد من الجوانب ولكنها توفر أمانًا أعلى من خلال استخدام قيم هاش أطول وإجراء معالجة أكثر تعقيدًا. إليك الخطوات الرئيسية لخوارزمية SHA-2:
- التعبئة: يتم أولاً تعبئة الرسالة الواردة لجعل طولها، ناقص 64 بت، يساوي 448 أو 896 على أساس مودولو 512 (لـ SHA-224 وSHA-256) أو مودولو 1024 (لـ SHA-384 وSHA-512). طريقة التعبئة هي نفسها المستخدمة في SHA-1، والتي تتضمن إضافة "1" في نهاية الرسالة، تليها عدة أصفار "0"، وأخيرًا تمثيل ثنائي بطول 64 بت (لـ SHA-224 وSHA-256) أو 128 بت (لـ SHA-384 وSHA-512) لطول الرسالة الأصلية بالبتات.
- تهيئة الذاكرة الوسيطة: تستخدم خوارزمية SHA-2 مجموعة من قيم الهاش المهيأة كذاكرة وسيطة بدءًا، اعتمادًا على متغير SHA-2 المختار. على سبيل المثال، يستخدم SHA-256 ثمانية سجلات 32 بت، بينما يستخدم SHA-512 ثمانية سجلات 64 بت. يتم تهيئة هذه السجلات إلى قيم ثابتة محددة.
- معالجة كتل الرسائل: يتم تقسيم الرسالة المعبأة إلى كتل بطول 512 بت أو 1024 بت، وتخضع كل كتلة لجولات متعددة من العمليات العملياتية. يؤدي SHA-256 وSHA-224 64 جولة من العمليات، بينما يؤدي SHA-512، SHA-384، SHA-512/224، وSHA-512/256 80 جولة. تتضمن كل جولة من العمليات سلسلة من العمليات البتية المعقدة، بما في ذلك العمليات المنطقية، الجمع الوحداتي، والعمليات الشرطية، معتمدة على وظائف غير خطية مختلفة وثوابت محددة مسبقًا. تزيد هذه العمليات من تعقيد وأمان الخوارزمية.
- الناتج: أخيرًا، بعد معالجة جميع الكتل، يتم دمج القيم في الذاكرة الوسيطة لتشكيل قيمة الهاش النهائية. اعتمادًا على متغير SHA-2، يمكن أن تكون قيمة الهاش هذه بطول 224، 256، 384، أو 512 بت.
قد تتساءل لماذا يمكن أن يكون إدخال إلى دالة الهاش بطول عشوائي، بينما الناتج ثابت. السبب هو أن عائلة SHA-2 تستخدم تحويل ميركل-دامغارد، الذي يسمح ببناء دوال الهاش التي يمكنها معالجة رسائل بأي طول من دالة الضغط ذات الطول الثابت. تم تبني تحويل ميركل-دامغارد في العديد من دوال الهاش التقليدية، بما في ذلك MD5 وSHA-1.
الفكرة الأساسية لتحويل ميركل-دامغارد هي تقسيم الرسالة الواردة إلى كتل ذات حجم ثابت ثم معالجة هذه الكتل واحدة تلو الأخرى، حيث يعتمد كل خطوة معالجة على نتيجة السابقة، في النهاية إنتاج قيمة هاش ذات حجم ثابت. تجسد خطوة التعبئة لـ SHA-256 المبادئ الأساسية لتحويل ميركل-دامغارد، أي من خلال التعبئة المناسبة لمعالجة الرسائل بأي طول وضمان أن يلبي طول الرسالة المعالجة النهائية شروطًا معينة (مثل كونها مضاعفًا لطول ثابت). وبالتالي، يمكن القول إن خطوة التعبئة لـ SHA-256 تتبع طريقة تحويل ميركل-دامغارد.
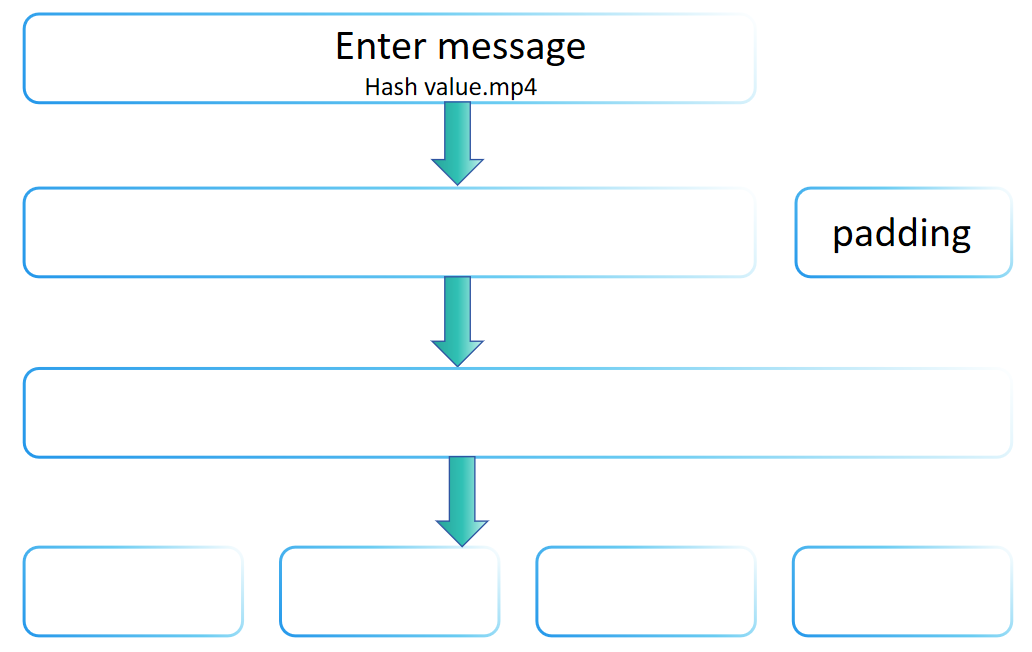
ومع ذلك، SHA-256 ليست مجرد تطبيق مباشر لتحويل ميركل-دامغارد. فهي تتضمن أيضًا سلسلة من الخطوات الحسابية المعقدة (مثل توسيع الرسالة، جولات متعددة من وظائف الضغط، وما إلى ذلك)، والتي هي تصميمات فريدة لـ SHA-256، بهدف تعزيز أمانها. وبالتالي، على الرغم من أن SHA-256 تتبع مبادئ تحويل ميركل-دامغارد في خطوة التعبئة الخاصة بها، إلا أنها تعزز الأمان العام من خلال تقديم آليات أمان أخرى، مما يجعلها لا تقتصر فقط على الإطار الأساسي لتحويل ميركل-دامغارد.
SHA-3 (خوارزمية الهاش الآمنة 3)
SHA-3 هو أحدث معيار للهاش الآمن، وقد تم اعتماده رسميًا من قبل المعهد الوطني للمعايير والتكنولوجيا (NIST) في عام 2015 كمعيار لمعالجة المعلومات الفيدرالية (FIPS 202). لا يهدف SHA-3 لاستبدال SHA-1 أو SHA-2 السابقين (حيث لا يزال SHA-2 يعتبر آمنًا)،
ولكن ليكون بمثابة تكملة ويقدم خيارًا بديلاً ضمن عائلة SHA، موفرًا خوارزمية هاش عملياتية مختلفة. يستند SHA-3 إلى خوارزمية Keccak، التي صممها Guido Bertoni وآخرون، وكانت الفائزة في مسابقة SHA-3 التي أقامتها NIST في عام 2012.
تختلف مبادئ عمل SHA-3 بشكل كبير عن SHA-2، وذلك لأنه يستخدم طريقة تعرف باسم "بنية الإسفنج" لامتصاص وعصر البيانات، مما ينتج عنه قيمة الهاش النهائية. تسمح هذه الطريقة لـ SHA-3 بإخراج قيم هاش بأطوال مختلفة، مما يوفر نطاقًا أوسع من التطبيقات مقارنةً بـ SHA-2. إليك الخطوات الرئيسية لخوارزمية SHA-3:
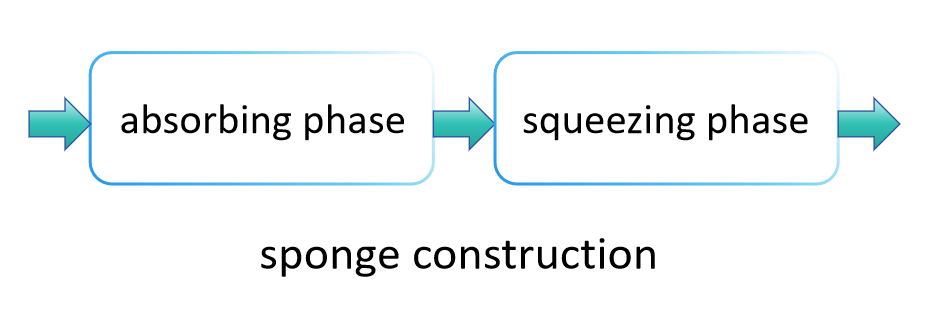
مرحلة الامتصاص:
في مرحلة الامتصاص، تقوم بنية الإسفنج أولاً بتقسيم البيانات الواردة إلى كتل ذات حجم ثابت. تُمتص هذه الكتل البيانية تتابعيًا في الحالة الداخلية للإسفنج، والتي تكون عادةً أكبر من كتلة بيانات واحدة، لضمان أنه يمكن معالجة كمية كبيرة من البيانات دون فيض. على وجه التحديد، يتم دمج كل كتلة بيانات مع جزء من الحالة الداخلية بطريقة ما (مثل عملية XOR)، يتبع ذلك تطبيق وظيفة التبديل الثابتة (في SHA-3، هذه هي Keccak-f ) لتحويل الحالة بالكامل، وبالتالي منع التداخل بين كتل البيانات الواردة المختلفة. يتم تكرار هذه العملية حتى يتم معالجة جميع كتل البيانات الواردة.
Keccak-f هي وظيفة التبديل الأساسية المستخدمة في خوارزمية الهاش العملياتية SHA-3. هي مكون مركزي في عائلة خوارزمية Keccak. يستند SHA-3 إلى خوارزمية Keccak، التي فازت بمسابقة الخوارزمية العملياتية التي أقامتها NIST وتم اختيارها كمعيار لـ SHA-3. تتضمن وظيفة Keccak-f عدة متغيرات، والأكثر استخدامًا هو Keccak-f[1600]، حيث يشير الرقم إلى عرض البتات الذي تعمل عليه.
Keccak-f تتألف من عدة جولات من نفس العملية (تُسمى الجولات). بالنسبة لـ Keccak-f[1600]، هناك 24 جولة من العمليات. كل جولة تشمل خمس خطوات أساسية: θ (theta)، ρ (rho)، π (pi)، χ (chi) و ι (iota). تعمل هذه الخطوات معًا على مصفوفة الحالة، تغير محتواها تدريجياً، مما يزيد من التشويش والانتشار لتعزيز الأمان. فيما يلي وصف موجز لهذه الخطوات:
- خطوة θ (ثيتا): تؤدي عمليات XOR على جميع بتات كل عمود، ثم تقوم بـ XOR النتيجة على الأعمدة المجاورة، مما يوفر انتشارًا بين الأعمدة.
- خطوة ρ (رو): عملية دوران على مستوى البت، حيث يتم تدوير كل بت عددًا مختلفًا من البتات وفقًا لقواعد محددة مسبقًا، مما يزيد من تعقيد البيانات.
- خطوة π (باي): تعيد ترتيب البتات في مصفوفة الحالة، تغيير موقع البتات لتحقيق انتشار عبر الصفوف والأعمدة.
- خطوة χ (كاي): خطوة غير خطية تؤدي عمليات XOR على كل بت من كل صف، بما في ذلك نفسه، جاره المباشر، ومكمل الجار. هذه عملية محلية تزيد من الخصائص غير الخطية للخوارزمية العملياتية.
- خطوة ι (يوتا): تقدم ثابت جولة إلى جزء من مصفوفة الحالة، مع اختلاف الثابت في كل جولة، لتجنب تشغيل جميع الجولات بشكل متطابق، مما يقدم عدم القابلية للتنبؤ.
توفر Keccak-f مستوى عالٍ من الأمان من خلال هذه الخطوات. يضمن تصميمها أن حتى التغييرات الطفيفة في الإدخال تؤدي إلى تغييرات واسعة النطاق وغير متوقعة في مصفوفة الحالة، والتي يتم تحقيقها من خلال مبادئ الارتباك (جعل من الصعب على المهاجمين استنتاج الإدخال من الإخراج) والانتشار (حيث تؤثر التغييرات الطفيفة في الإدخال على أجزاء متعددة من الإخراج).
يسمح تصميم Keccak-f بتعديل المعلمات (مثل حجم الحالة وعدد الجولات) عبر مستويات أمان مختلفة وسيناريوهات تطبيقية، مما يوفر مرونة كبيرة. Keccak-f[1600] مشهورة بتنفيذها الفعال، حيث تحقق سرعات معالجة عالية سواء في الأجهزة أو في البرمجيات، خاصة عند التعامل مع كميات كبيرة من البيانات.
مرحلة العصر:
بمجرد استيعاب جميع كتل البيانات الواردة في الحالة الداخلية، تدخل بنية الإسفنج مرحلة العصر. في هذه المرحلة، يتم إخراج أجزاء من الحالة الداخلية تدريجيًا كنتيجة لدالة الهاش. إذا تجاوز الطول المطلوب للإخراج الكمية التي يمكن عصرها دفعة واحدة، تطبق بنية الإسفنج وظيفة التبديل لتحويل الحالة الداخلية مرة أخرى، ثم تستمر في إخراج المزيد من البيانات. يستمر هذا العمل حتى يتم الوصول إلى طول الإخراج المطلوب.
الهدف من تصميم SHA-3 هو توفير أمان أعلى من SHA-2 ومقاومة أفضل ضد هجمات الحوسبة الكمومية. بفضل بنيته الإسفنجية الفريدة، يُعتقد نظريًا أن SHA-3 قادر على مقاومة جميع أساليب الهجوم العملياتية المعروفة حاليًا، بما في ذلك هجمات التصادم، هجمات الصورة المسبقة، وهجمات الصورة المسبقة الثانية.
RIPEMD-160 (تقييم رسالة دوال النزاهة العملياتية)
RIPEMD-160 هي دالة هاش عملياتية صُممت لتوفير خوارزمية هاش آمنة. تم تطويرها في عام 1996 بواسطة هانس دوبرتين وآخرين، وهي جزء من عائلة RIPEMD (تقييم رسالة دوال النزاهة العملياتية).
ينتج RIPEMD-160 قيمة هاش بطول 160 بت (20 بايت)، وهو ما يُفسر "160" في اسمه. يستند إلى تصميم MD4 وتأثر بخوارزميات هاش أخرى مثل MD5 وSHA-1. يتضمن RIPEMD-160 عمليتين موازيتين، متشابهتين تعالجان البيانات الواردة بشكل منفصل ثم تجمعان نتائج هاتين العمليتين لتوليد قيمة الهاش النهائية. تهدف هذه التصميم إلى تعزيز الأمان.
تتضمن عملية حساب RIPEMD-160 عدة خطوات أساسية: التعبئة، معالجة الكتل، والضغط:
- التعبئة: يتم أولاً تعبئة الرسالة الواردة لضمان أن طولها مضروبا في 512 بت يساوي 448 بت. التعبئة تبدأ دائمًا ببت واحد من 1 يليها سلسلة من الأصفار 0، تنتهي بتمثيل 64 بت لطول الرسالة الأصلية.
- معالجة الكتل: يتم تقسيم الرسالة المعبأة إلى كتل 512 بت.
- التهيئة: يستخدم خمسة سجلات 32 بت (A, B, C, D, E)، والتي يتم تهيئتها إلى قيم محددة معينة.
- وظيفة الضغط: يتم معالجة كل كتلة بدورها، تحديث قيم هذه السجلات الخمسة من خلال سلسلة من العمليات المعقدة. تتضمن هذه العملية عمليات بتية (مثل الجمع، وAND، وOR، وNOT، والتحولات الدائرية اليسرى) واستخدام مجموعة من الثوابت الثابتة.
- الناتج: بعد معالجة جميع الكتل، يتم ربط قيم هذه السجلات الخمسة لتشكيل القيمة النهائية للهاش بطول 160 بت.