Was ist ein Hash-Wert?

Ein Hash-Wert ist eine feste Zeichenkette oder Zahl, die von beliebigen Eingabedaten mittels einer Hash-Funktion generiert wird. Diese Funktionen akzeptieren verschiedene Eingaben wie Texte, Bilder und Videos und erzeugen einen festen, nicht umkehrbaren Hash-Wert. Hash-Werte sind deterministisch, was bedeutet, dass identische Eingaben immer denselben Ausgang erzeugen. Sie bieten auch Kollisionsschutz, was es herausfordernd macht, unterschiedliche Eingaben zu finden, die denselben Ausgang ergeben.

Funktionen des Hash-Werts

Hash-Werte spielen eine wesentliche Rolle in der Informatik und der IT, indem sie eine feste Zusammenfassung von Daten unabhängig von deren Größe bieten. Diese Funktionen erleichtern verschiedene Anwendungen:

• Datenintegritätsprüfung: Wird verwendet, um zu überprüfen, ob Daten während der Übertragung unverändert bleiben und die Integrität heruntergeladener Dateien zu gewährleisten.
• Passwortspeicherung: Passwörter werden als Hash-Werte zur Sicherheit gespeichert, was es schwierig macht, originale Passwörter aus kompromittierten Datenbanken wiederherzustellen.
• Schnelle Datenabruf: Hash-Werte dienen als Indizes in Hashtabellen und ermöglichen effiziente Datenoperationen.
• Datendeduplizierung: Hilft bei der Identifizierung und Entfernung von Duplikaten durch Vergleich von Hash-Werten.
• Digitale Signatur und Überprüfung: Gewährleistet Datenintegrität und -herkunft durch Public-Key-Kryptografie und Hash-Funktionen.
• Blockchain-Technologie: Nutzt Hash-Werte zur Sicherung von Transaktionsdatensätzen und zur Gewährleistung der Unveränderlichkeit von Daten.
• Fälschungssichere Zeitstempel: Bietet einen unumkehrbaren Zeitstempel für Daten, der in rechtlichen und urheberrechtlichen Schutzmaßnahmen nützlich ist.

Der Grund, warum Hash-Werte in diesen Bereichen effektiv sind, liegt in ihren Schlüsselmerkmalen von Geschwindigkeit, Determinismus, Unumkehrbarkeit und Kollisionsschutz. Bei ordnungsgemäßer Verwendung können Hash-Funktionen robuste Unterstützung bei der Sicherung von Daten, der Verbesserung der Effizienz und der Überprüfung der Authentizität von Informationen bieten.

Was ist eine Hash-Funktion?

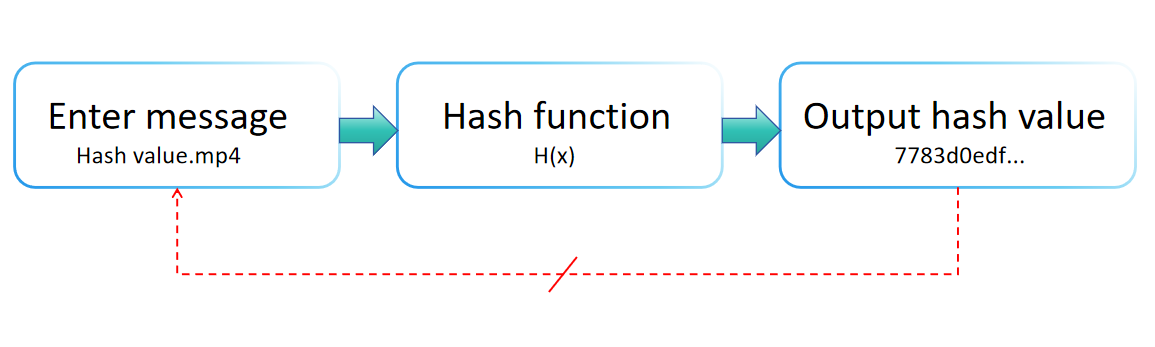
Eine Hash-Funktion ist eine mathematische Konstruktion, die Eingabedaten (oder "Nachrichten") auf eine feste Zeichenfolge abbildet, typischerweise einen numerischen Wert, wie im folgenden Diagramm dargestellt. Weit verbreitet in der Datenverwaltung und Informationssicherheit, zeichnet sich eine Hash-Funktion durch ihre effiziente Rechenleistung, konsistente Ausgabelänge, Unumkehrbarkeit, Empfindlichkeit gegenüber Eingabevariationen und Kollisionsbeständigkeit aus.

Effiziente Rechenleistung

Hash-Funktionen können schnell Hash-Werte aus Daten jeder Form berechnen, unabhängig von der Größe der Daten. Diese Eigenschaft ist entscheidend für Anwendungen, die einen schnellen Zugriff auf Daten erfordern, wie z. B. Hashtabellen. Dies liegt daran, dass die Geschwindigkeit der Hash-Funktion bei der Speicherung von Daten in Hashtabellen die Geschwindigkeit des Datenabrufs bestimmt. Hashtabellen verwenden Hash-Funktionen, um schnell den Speicherort der Daten zu lokalisieren, wobei sie auf die schnelle Rechenfähigkeit von Hash-Funktionen vertrauen.

Darüber hinaus beeinflusst die Effizienz von Hash-Funktionen direkt die Gesamtleistung eines Systems, das große Datenmengen verarbeiten muss. Wenn eine Hash-Funktion langsam ausgeführt wird, wird sie zu einem Engpass in der Systemleistung. Einige Echtzeitsysteme, wie die Paketfilterung in Netzwerkgeräten, erfordern die sofortige Berechnung von Hash-Werten für Daten, um schnelle Entscheidungen zu treffen. In diesen Fällen ist die Effizienz von Hash-Funktionen gleichermaßen wichtig.

Nehmen Sie beispielsweise eine Online-E-Commerce-Plattform, auf der Benutzer Produktbezeichnungen in die Suchleiste eingeben, um Produkte zu finden. Das Backend-System kann Hash-Funktionen verwenden, um schnell Produktinformationen zu lokalisieren, die in Hashtabellen gespeichert sind. Wenn der Prozess der Hash-Funktionsberechnung langsam ist, wird die Benutzererfahrung stark beeinträchtigt, da die Benutzer länger auf Suchergebnisse warten müssen. In dieser Situation gewährleistet die effiziente Rechenleistung von Hash-Funktionen schnelle Reaktionszeiten und verbessert so die Benutzererfahrung. [Erfahren Sie mehr]

Konsistenz der Ausgabelänge bei Hash-Funktionen

Hash-Funktionen wandeln Eingaben beliebiger Länge durch eine komplexe Abfolge von Berechnungen in eine Ausgabe fester Länge um. Dieser Prozess umfasst oft das Aufteilen der Eingabedaten in Blöcke fester Größe (für Eingaben, die die Größe der Verarbeitungseinheit überschreiten), das Anwenden einer Reihe von mathematischen und logischen Operationen auf jeden Block und das anschließende Kombinieren oder Akkumulieren der Ergebnisse dieser Operationen auf irgendeine Weise, um letztendlich einen Hash-Wert fester Größe zu erzeugen.

Warum ist das wichtig? Die Konsistenz der Ausgabelänge trägt dazu bei, die Sicherheit von Hash-Funktionen zu gewährleisten. Wenn die Länge der Hash-Ausgabe variieren könnte, könnte dies Informationen über die Größe der Originaldaten preisgeben, was in einigen Szenarien möglicherweise ausgenutzt werden könnte, um das System anzugreifen. Darüber hinaus erschwert eine feste Ausgabelänge es Angreifern, Eigenschaften der Eingabedaten anhand der Ausgabelänge zu ermitteln. Gleichzeitig vereinfachen feste Ausgabelängen die Speicherung und den Vergleich von Hash-Werten. Systemdesigner können im Voraus wissen, wie viel Platz jeder Hash-Wert einnehmen wird, was für Szenarien wie Datenbankdesign und Netzwerkübertragung sehr wichtig ist. Darüber hinaus ist die Konsistenz der Ausgabelänge sehr effizient für den Vergleich von Hash-Werten, da nur Daten fester Länge verglichen werden müssen. Dies ist besonders wichtig bei der Verwendung von Hashtabellen für schnelle Datenabrufe.

Nehmen Sie zum Beispiel SHA-256 als Beispiel. Diese weit verbreitete kryptografische Hash-Funktion erzeugt immer einen 256-Bit (d. h. 32-Byte) Hash-Wert, unabhängig davon, ob die Eingabedaten ein einzelnes Byte oder mehrere Millionen Bytes umfassen. Diese Konsistenz gewährleistet, dass SHA-256-Hash-Werte für verschiedene Sicherheitsanwendungen verwendet werden können, wie zum Beispiel digitale Signaturen und Message Authentication Codes (MACs), während gleichzeitig der Datenverarbeitungs- und Speicherungsworkflow vereinfacht wird.

Irreversibilität von Hash-Funktionen

Hash-Funktionen sind unidirektional, was bedeutet, dass es unmöglich ist, aus dem Hash-Wert die Originaldaten abzuleiten. Diese Eigenschaft ist besonders wichtig beim Speichern von Passwörtern, da selbst bei Kompromittierung der Datenbank Angreifer die Passwörter nicht aus den Hash-Werten wiederherstellen können. Die Irreversibilität von Hash-Funktionen basiert hauptsächlich auf den folgenden Prinzipien und Merkmalen:

• Kompression: Hash-Funktionen können Eingaben beliebiger Länge (die in der praktischen Anwendung sehr groß sein können) auf eine Ausgabe fester Länge abbilden. Dies bedeutet, dass unendlich viele mögliche Eingaben auf eine endliche Anzahl von Ausgaben abgebildet werden. Da der Ausgaberaum (Hash-Werte) viel kleiner ist als der Eingaberaum, werden verschiedene Eingaben zwangsläufig denselben Ausgang (Hash-Wert) erzeugen, ein Phänomen, das als "Kollision" bekannt ist. Aufgrund dieser Kompression ist es unmöglich, die spezifische Eingabe aus einem gegebenen Ausgang (Hash-Wert) zu bestimmen.
• Hohe Nichtlinearität und Komplexität: Hash-Funktionen werden unter Verwendung komplexer mathematischer und logischer Operationen (wie bitweise Operationen, Modulo-Operationen usw.) entwickelt, um sicherzustellen, dass die Ausgabe sehr empfindlich auf die Eingabe reagiert. Selbst geringfügige Änderungen an der Eingabe (z. B. Änderung eines Bits) können signifikante und unvorhersehbare Änderungen an der Ausgabe (dem Hash-Wert) bewirken. Diese hohe Nichtlinearität und die Zufälligkeit der Ausgabe machen es äußerst schwierig, die Originaldaten aus dem Hash-Wert abzuleiten.
• Unidirektionalität: Die Gestaltung von Hash-Funktionen gewährleistet, dass ihr Betrieb einseitig ist; das heißt, während die Berechnung des Hash-Werts einfach ist, ist der umgekehrte Prozess (das Wiederherstellen der Originaldaten aus dem Hash-Wert) nicht durchführbar. Dies liegt daran, dass der Berechnungsprozess von Hash-Funktionen eine Reihe von irreversiblen Operationen (wie die Unumkehrbarkeit von Modulo-Operationen) umfasst, die sicherstellen, dass es selbst mit dem Hash-Wert unmöglich ist, die Originaldaten umzukehren.
• Zufällige Zuordnung: Eine ideale Hash-Funktion sollte als "zufälliger Mapper" fungieren, was bedeutet, dass jede mögliche Eingabe gleich wahrscheinlich auf jeden Punkt im Ausgaberaum abgebildet wird. Diese Eigenschaft stellt sicher, dass es keine praktikable Möglichkeit gibt, vorherzusagen, auf welchen Ausgang eine bestimmte Eingabe abgebildet wird, was die Unumkehrbarkeit der Hash-Funktion erhöht.
• Mathematische Grundlage: Mathematisch lässt sich die Unumkehrbarkeit von Hash-Funktionen durch ihre Abhängigkeit von "diskreten Logarithmusproblemen," "großen Integerfaktorisierungsproblemen" oder anderen zahlentheoretischen Problemen verstehen, die mit den aktuellen mathematischen und rechnerischen Möglichkeiten schwer zu lösen sind. Die Gestaltung einiger Hash-Algorithmen kann beispielsweise indirekt von der Berechnungsschwierigkeit dieser Probleme abhängen, wodurch ihre Unumkehrbarkeit sichergestellt wird.

Eingabesensitivität und der Lawineneffekt

Bei der Gestaltung von Hash-Funktionen werden komplexe mathematische und logische Operationen (wie bitweise Operationen, Modulo-Operationen usw.) verwendet, um sicherzustellen, dass die Ausgabe sehr empfindlich auf die Eingabe reagiert. Selbst geringfügige Änderungen an der Eingabe (zum Beispiel das Ändern eines einzelnen Bits) führen zu signifikanten und unvorhersehbaren Veränderungen in der Ausgabe (dem Hash-Wert), ein Phänomen, das als "Lawineneffekt" bekannt ist. [Erfahren Sie mehr]

Kollisionsresistenz in der Kryptographie

Die Kollisionsresistenz einer Hash-Funktion ist ein entscheidendes Konzept in der Kryptographie und zeigt das Sicherheitsniveau einer Hash-Funktion gegen Kollisionsangriffe an. Diese Eigenschaft bedeutet, dass es für jede Hash-Funktion H praktisch unmöglich ist, zwei verschiedene Eingaben x und y (x ≠ y) zu finden, für die H(x) = H(y) gilt. Eine Hash-Funktion mit robuster Kollisionsresistenz macht es äußerst schwierig, zwei verschiedene Eingaben zu finden, die denselben Ausgabewert erzeugen.

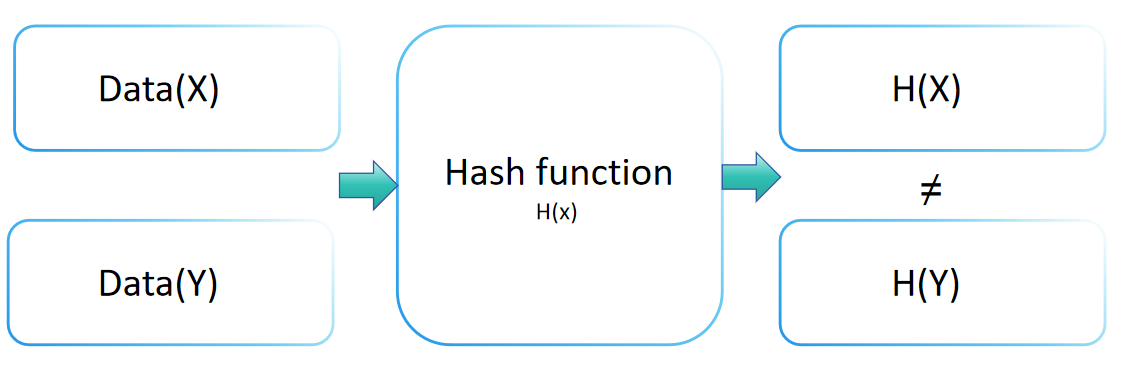
Die Kollisionsresistenz spielt eine entscheidende Rolle bei der Aufrechterhaltung der Datenintegrität und -überprüfung. Durch die Umwandlung von Eingabeinformationen in eine Ausgabe fester Größe (oder einen Digest) stellen Hash-Funktionen sicher, dass keine zwei verschiedenen Eingaben dieselbe Ausgabe erzeugen. Diese einzigartige Eigenschaft ermöglicht es, den Hash-Wert genau dem ursprünglichen Wert zuzuordnen.

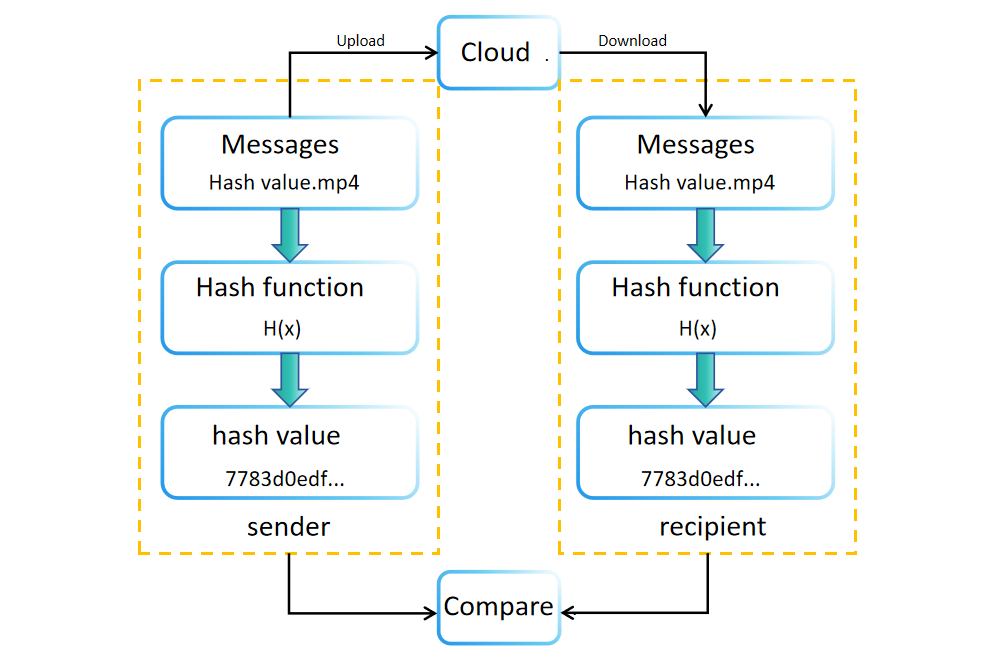
Während der Datenerstellung oder -speicherung wird ein Hash-Wert (oder Digest) mithilfe einer Hash-Funktion generiert. Dieser Wert wird neben den ursprünglichen Daten gespeichert oder übertragen. Beispielsweise zeigen Software-Downloadseiten häufig Datei-Hash-Werte zur Integritätsüberprüfung an. Empfänger können unabhängig den empfangenen Datenwert neu berechnen, um dessen Integrität zu bestätigen. Stimmen die ursprünglichen und neu berechneten Hash-Werte überein, ist die Integrität der Daten bestätigt. Andernfalls wurden die Daten möglicherweise während der Übertragung oder Speicherung manipuliert oder beschädigt.

Der Vergleich von Hash-Werten bietet auch den Vorteil, die Datenintegrität ohne erheblichen Speicherplatzbedarf zu überprüfen. Diese Methode ermöglicht es Empfängern, die Echtheit von Daten zu bestätigen, indem sie einfach die Hash-Werte vor und nach der Übertragung vergleichen.

Können Hash-Kollisionen gefunden werden?

Durch die oben genannten Eigenschaften der Hash-Funktionen haben wir die Kollisionsresistenz verstanden. Aber ist es möglich, dass Hash-Kollisionen existieren, das heißt, dass zwei verschiedene Eingaben denselben Ausgang erzeugen? Die Antwort ist ja, Kollisionen existieren tatsächlich. Gemäß dem Schubfachprinzip gibt es bei ausreichend großem Eingaberaum die Möglichkeit von Hash-Kollisionen. Dies liegt daran, dass der Ausgaberaum von Hash-Funktionen in der Regel viel kleiner ist als der Eingaberaum, was zwangsläufig dazu führt, dass mehrere verschiedene Eingaben auf denselben Ausgang abgebildet werden.

Das Schubfachprinzip ist ein einfaches und intuitives Prinzip der kombinatorischen Mathematik, das besagt, dass, wenn mehr als n Objekte in n Behälter gelegt werden, dann mindestens ein Behälter zwei oder mehr Objekte enthält. Dieses Prinzip kann auch verwendet werden, um Probleme wie das Geburtstagsparadoxon zu erklären.

Die Anwendung des Schubfachprinzips ist sehr breit gefächert und hat wichtige Anwendungen in Bereichen wie Kryptographie, Informatik und Mathematik. Zum Beispiel wird in der Informatik das Schubfachprinzip verwendet, um die Korrektheit bestimmter Algorithmen zu beweisen oder die Zeitkomplexität von Algorithmen zu analysieren. In der Kryptographie wird das Schubfachprinzip ebenfalls verwendet, um bestimmte kryptographische Angriffsmethoden zu entwerfen, wie etwa den Geburtstagsangriff.

Das Geburtstagsparadoxon ist eine klassische Anwendung des Schubfachprinzips. Angenommen, es gibt n Personen in einem Raum. Wenn wir möchten, dass die Wahrscheinlichkeit, dass mindestens zwei Personen denselben Geburtstag haben, größer als 50 % ist, wie viele Personen werden benötigt? Gemäß dem Schubfachprinzip, wenn 367 Personen (unter der Annahme, dass es 366 Tage im Jahr gibt, plus einen zusätzlichen Tag für den 29. Februar in einem Schaltjahr) in 366 "Schubfächer" (d. h. Geburtstage) gelegt werden, wird mindestens ein "Schubfach" zwei Personen enthalten, was bedeutet, dass mindestens zwei Personen denselben Geburtstag haben. Dies verdeutlicht das Geburtstagsparadoxon.

Es ist wichtig zu beachten, dass, obwohl das Schubfachprinzip einfach und intuitiv ist, dessen Anwendung den spezifischen Kontext berücksichtigen muss. Beispielsweise ist es bei der Anwendung des Schubfachprinzips notwendig sicherzustellen, dass die beteiligten Zufallsvariablen voneinander unabhängig sind; andernfalls kann dies zu falschen Schlussfolgerungen führen. Darüber hinaus ist es in einigen Fällen auch notwendig, Faktoren wie die Größe und Form der Schubfächer zu berücksichtigen.

Allerdings ist es möglicherweise nicht praktisch, Hash-Kollisionen einfach durch das Durchlaufen des Eingaberaums zu finden, hauptsächlich aus zwei Gründen:

• Berechnungskomplexität: Für die meisten Hash-Funktionen ist der Eingaberaum enorm groß. Nehmen wir SHA-256 als Beispiel; sein Ausgang ist ein 256-Bit-Hash-Wert, was bedeutet, dass es 2^256 mögliche Ausgänge gibt. Da eines der Entwurfsziele von Hash-Funktionen darin besteht, Kollisionen so weit wie möglich zu minimieren, wäre es theoretisch notwendig, etwa 2^(256/2) = 2^128 Eingaben zu durchlaufen, um eine Kollision für SHA-256 zu finden, gemäß dem Geburtstagsparadoxon, was die ungefähre erwartete Anzahl von Eingaben ist, um eine Kollision zu finden. Selbst mit den leistungsfähigsten Supercomputern, die derzeit verfügbar sind, würde es weit über ein menschliches Leben dauern, eine solche Aufgabe zu erledigen, sodass es als unmöglich gilt, eine SHA-256-Hash-Kollision durch einfaches Durchlaufen zu finden.
• Entwurf von Hash-Funktionen: Hash-Funktionen sind typischerweise so konzipiert, dass das Auffinden von Kollisionen rechnerisch unmöglich ist. Dies bedeutet, dass, obwohl Kollisionen theoretisch existieren, sie in der Praxis praktisch unmöglich zu finden sind. Dies ist eine wichtige Eigenschaft kryptographischer Hash-Funktionen (wie SHA-256), die weit verbreitet in Bereichen wie digitalen Signaturen, Passwortspeicherung und mehr verwendet werden.

Natürlich können wir auch spezifische Algorithmen verwenden, um Hash-Kollisionen zu finden. Diese Algorithmen nutzen oft bekannte Eigenschaften oder Schwächen von Hash-Funktionen aus, um Kollisionen zu finden. Hier sind einige gängige Techniken und Methoden zum Auffinden von Hash-Kollisionen:

• Geburtstagsangriff: Dies ist eine wahrscheinlichkeitsbasierte einfache Methode, die verwendet wird, um die Zeit abzuschätzen, die zum Finden einer Kollision benötigt wird, wenn Eingaben zufällig ausgewählt werden. Das Prinzip des Geburtstagsangriffs besagt, dass bei vielen Menschen in einem Raum die Wahrscheinlichkeit, dass zwei Personen denselben Geburtstag haben, mit der Anzahl der Personen zunimmt. Ähnlich wie bei Hash-Funktionen, wenn eine ausreichende Anzahl von Eingaben zufällig ausgewählt wird, ist es wahrscheinlich, dass zwei Eingaben letztendlich denselben Hash-Wert erzeugen.
• Brute-Force-Angriff: Dies ist die einfachste Methode, die darin besteht, alle möglichen Eingaben zu durchlaufen, um eine Kollision zu finden. Diese Methode ist jedoch für Hash-Funktionen mit großen Eingaberäumen aufgrund des enormen Bedarfs an Rechenressourcen und Zeit nicht praktikabel.
• Regenbogentabellen: Diese Technik wird verwendet, um eine große Anzahl von Hash-Werten und ihren entsprechenden Eingaben vorab zu berechnen und zu speichern. Regenbogentabellen sind besonders nützlich zum Knacken von Passwörtern, die keine zufällige Datenverschleierung verwendet haben oder eine bekannte Hash-Funktion haben. Durch das Nachschlagen in der Regenbogentabelle kann ein Angreifer schnell eine Eingabe finden, die mit einem bestimmten Hash-Wert übereinstimmt.
• Hash-Verlängerungsangriffe: Bestimmte Hash-Funktionen ermöglichen es Angreifern, zusätzliche Daten mit einem bekannten Hash-Wert zu kombinieren, ohne die ursprüngliche Eingabe zu kennen, und damit einen neuen Hash-Wert zu generieren. Dieser Angriff kann verwendet werden, um Kollisionen zu konstruieren oder andere Arten von Angriffen durchzuführen.
• Speziell konstruierte Eingaben: Manchmal können Angreifer spezifische Schwächen oder nichtlineare Verhaltensweisen in Hash-Funktionen ausnutzen, um spezielle Eingaben zu konstruieren, die wahrscheinlicher sind, Kollisionen in der Hash-Funktion zu erzeugen.

Welche Hash-Funktionen werden häufig verwendet?

MD5 (Message Digest Algorithm 5)

MD5 ist eine weit verbreitete kryptographische Hash-Funktion, die von Ronald Rivest in den 1990er Jahren entwickelt wurde, um den älteren MD4-Algorithmus zu ersetzen. Sie kann eine Nachricht beliebiger Länge in einen Hash-Wert fester Länge (128 Bit oder 16 Bytes) umwandeln. Das Entwurfsziel von MD5 war es, einen schnellen und relativ sicheren Weg zur Generierung eines digitalen Fingerabdrucks von Daten bereitzustellen. Es wurden jedoch Kollisionsmethoden für MD5 entdeckt, was den Algorithmus unsicher macht, aber er wird immer noch weit verbreitet eingesetzt, wenn Sicherheit keine primäre Rolle spielt.

Der Berechnungsprozess von MD5 umfasst folgende Schritte:

• Padding: Zunächst wird die originale Daten mit Nullen aufgefüllt, sodass ihre Bytelänge ein Vielfaches von 512 ist. Das Padding beginnt mit einer 1, gefolgt von Nullen, bis die Längenanforderung erfüllt ist.
• Länge hinzufügen: Ein 64-Bit-Längenwert, der die binäre Darstellung der ursprünglichen Nachrichtenlänge ist, wird zur gepaddeten Nachricht hinzugefügt, sodass die endgültige Nachrichtenlänge ein Vielfaches von 512 Bit ist.
• Initialisierung des MD-Puffers: Vier 32-Bit-Register (A, B, C, D) werden initialisiert, um die Zwischen- und Endhash-Werte zu speichern.
• Verarbeitung von Nachrichtenblöcken: Die gepaddete und längenverarbeitete Nachricht wird in 512-Bit-Blöcke unterteilt, und jeder Block wird durch vier Runden von Operationen verarbeitet. Jede Runde umfasst 16 ähnliche Operationen basierend auf nichtlinearen Funktionen (F, G, H, I), linken zyklischen Schiebeoperationen und Addition modulo 32.
• Ergebnis: Der endgültige Hash-Wert ist der Inhalt des letzten Zustands der vier Register A, B, C, D, die zusammengefügt werden (jedes Register ist 32 Bit lang), um einen 128-Bit-Hash-Wert zu bilden.

SHA-1 (Secure Hash Algorithm 1)

SHA-1 wurde von der US-amerikanischen National Security Agency (NSA) entworfen und 1995 als Federal Information Processing Standard (FIPS PUB 180-1) vom National Institute of Standards and Technology (NIST) veröffentlicht. SHA-1 ist für den Einsatz in digitalen Signaturen und anderen kryptografischen Anwendungen gedacht und erzeugt einen 160-Bit (20-Byte) Hash-Wert, der als Nachrichten-Prüfsumme bekannt ist. Obwohl bekannt ist, dass SHA-1 Sicherheitsanfälligkeiten aufweist und durch sicherere Algorithmen wie SHA-256 und SHA-3 ersetzt wurde, hat das Verständnis seines Arbeitsprinzips immer noch einen Bildungs- und historischen Wert.

Der Entwurfszweck von SHA-1 besteht darin, eine Nachricht beliebiger Länge zu nehmen und eine 160-Bit-Nachrichten-Prüfsumme zu erzeugen, um die Integrität der Daten zu überprüfen. Sein Berechnungsprozess kann in folgende Schritte unterteilt werden:

• Padding: Zunächst wird die ursprüngliche Nachricht mit Nullen aufgefüllt, sodass ihre Länge (in Bits) modulo 512 gleich 448 ist. Das Padding beginnt immer mit einem "1"-Bit, gefolgt von mehreren "0"-Bits, bis die obige Längenbedingung erfüllt ist.
• Länge hinzufügen: Ein 64-Bit-Block wird zur gepaddeten Nachricht hinzugefügt, der die Länge der ursprünglichen Nachricht (in Bits) darstellt, sodass die endgültige Nachrichtenlänge ein Vielfaches von 512 Bit ist.
• Initialisierung des Buffers: Der SHA-1-Algorithmus verwendet einen 160-Bit-Puffer, der in fünf 32-Bit-Register (A, B, C, D, E) unterteilt ist, um die Zwischen- und Endhash-Werte zu speichern. Diese Register werden zu Beginn des Algorithmus auf bestimmte Konstantenwerte initialisiert.
• Verarbeitung von Nachrichtenblöcken: Die vorverarbeitete Nachricht wird in 512-Bit-Blöcke unterteilt. Für jeden Block führt der Algorithmus eine Hauptschleife mit 80 ähnlichen Schritten aus. Diese 80 Schritte sind in vier Runden unterteilt, jede mit 20 Schritten. Jeder Schritt verwendet eine andere nichtlineare Funktion (F, G, H, I) und eine Konstante (K). Diese Funktionen sind so konzipiert, dass sie die Komplexität und Sicherheit der Operationen erhöhen. In diesen Schritten verwendet der Algorithmus bitweise Operationen (wie UND, ODER, XOR, NICHT) und Addition modulo 32 sowie links zirkuläre Verschiebungen.
• Ergebnis: Nach der Verarbeitung aller Blöcke werden die akkumulierten Werte in den fünf Registern zu einem endgültigen 160-Bit-Hash-Wert zusammengefügt.

SHA-2 (Secure Hash Algorithm 2)

SHA-2 ist eine Familie kryptographischer Hash-Funktionen, die mehrere verschiedene Versionen umfasst und hauptsächlich aus sechs Varianten besteht: SHA-224, SHA-256, SHA-384, SHA-512, SHA-512/224 und SHA-512/256. SHA-2 wurde von der National Security Agency (NSA) der Vereinigten Staaten entworfen und vom National Institute of Standards and Technology (NIST) als Federal Information Processing Standard (FIPS) veröffentlicht. Im Vergleich zu seinem Vorgänger, SHA-1, bietet SHA-2 erhöhte Sicherheit, die sich hauptsächlich in längeren Hash-Werten und einer stärkeren Resistenz gegen Kollisionsangriffe zeigt.

Der Betrieb der SHA-2-Familie ähnelt in vielen Aspekten SHA-1, bietet jedoch durch die Verwendung längerer Hash-Werte und eines komplexeren Verarbeitungsverfahrens eine höhere Sicherheit. Hier sind die Hauptschritte des SHA-2-Algorithmus:

• Padding: Die Eingabebotschaft wird zunächst aufgefüllt, um ihre Länge abzüglich 64 Bits auf der Basis eines Modulo-512 (für SHA-224 und SHA-256) oder Modulo-1024 (für SHA-384 und SHA-512) gleich 448 oder 896 zu machen. Die Polsterungsmethode ist dieselbe wie bei SHA-1, bei der am Ende der Nachricht eine "1" hinzugefügt wird, gefolgt von mehreren "0", und schließlich eine 64-Bit (für SHA-224 und SHA-256) oder 128-Bit (für SHA-384 und SHA-512) Binärdarstellung der ursprünglichen Nachrichtenlänge in Bits.
• Initialisierung des Buffers: Der SHA-2-Algorithmus verwendet eine Reihe initialisierter Hash-Werte als Ausgangsbuffer, abhängig von der gewählten SHA-2-Variante. Beispielsweise verwendet SHA-256 acht 32-Bit-Register, während SHA-512 acht 64-Bit-Register verwendet. Diese Register werden auf bestimmte Konstantenwerte initialisiert.
• Verarbeitung von Nachrichtenblöcken: Die aufgefüllte Nachricht wird in 512-Bit- oder 1024-Bit-Blöcke unterteilt, und jeder Block durchläuft mehrere Runden kryptografischer Operationen. SHA-256 und SHA-224 führen 64 Runden von Operationen aus, während SHA-512, SHA-384, SHA-512/224 und SHA-512/256 80 Runden durchführen.Jede Runde der Operation enthält eine Reihe komplexer bitweiser Operationen, einschließlich logischer, modularer Addition und bedingter Operationen, die auf unterschiedlichen nichtlinearen Funktionen und vordefinierten Konstanten beruhen. Diese Operationen erhöhen die Komplexität und Sicherheit des Algorithmus.
• Ausgabe: Schließlich werden nach Verarbeitung aller Blöcke die Werte im Buffer kombiniert, um den endgültigen Hash-Wert zu bilden. Abhängig von der SHA-2-Variante kann dieser Hash-Wert 224, 256, 384 oder 512 Bits lang sein.

Sie fragen sich vielleicht, warum die Eingabe einer Hash-Funktion beliebiger Länge sein kann, aber die Ausgabe festgelegt ist. Der Grund dafür ist, dass die SHA-2-Familie die Merkle-Damgård-Transformation verwendet, die die Konstruktion von Hash-Funktionen ermöglicht, die Nachrichten beliebiger Länge aus einer Kompressionsfunktion fester Länge verarbeiten können. Die Merkle-Damgård-Transformation wird in vielen traditionellen Hash-Funktionen, einschließlich MD5 und SHA-1, verwendet.

Die Kernidee der Merkle-Damgård-Transformation besteht darin, die Eingabemeldung in Blöcke fester Größe zu unterteilen und diese Blöcke nacheinander zu verarbeiten, wobei jeder Verarbeitungsschritt vom Ergebnis des vorherigen abhängt und schließlich einen Hash-Wert fester Größe produziert. Der Polsterschritt von SHA-256 verkörpert die grundlegenden Prinzipien der Merkle-Damgård-Transformation, nämlich, durch geeignetes Polstern, um Nachrichten beliebiger Länge zu verarbeiten, und Sicherstellen, dass die endgültige verarbeitete Nachrichtenlänge bestimmte Bedingungen erfüllt (wie ein Vielfaches einer festen Länge). Daher kann gesagt werden, dass der Polsterschritt von SHA-256 dem Verfahren der Merkle-Damgård-Transformation folgt.

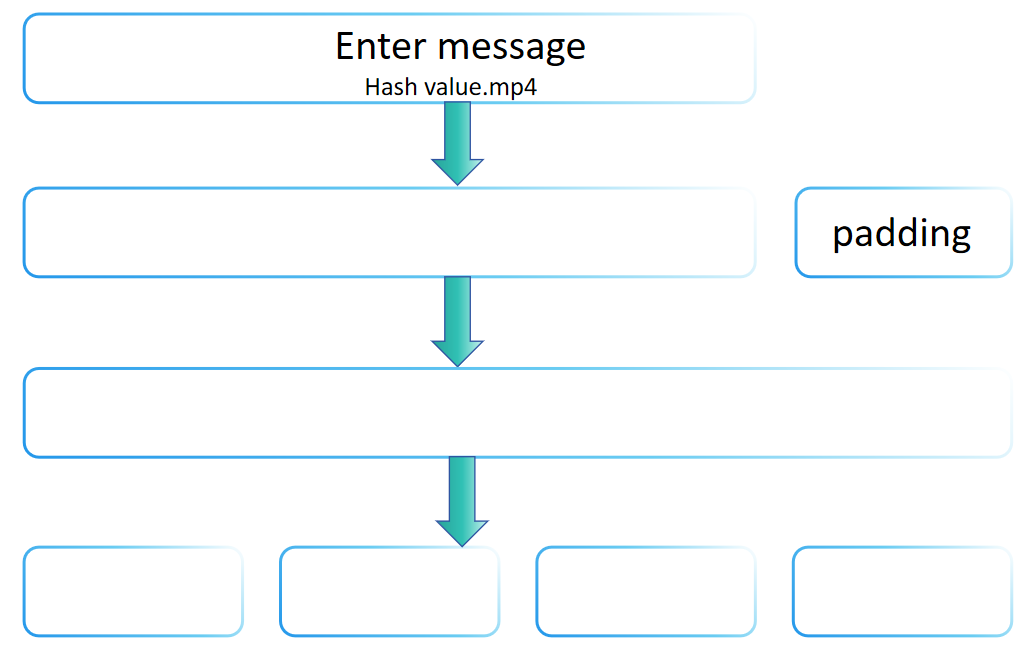
Jedoch ist SHA-256 nicht nur eine direkte Implementierung der Merkle-Damgård-Transformation. Er umfasst auch eine Reihe komplexer Berechnungsschritte (wie Nachrichtenerweiterung, mehrere Runden von Kompressionsfunktionen usw.), die einzigartige Designs von SHA-256 sind, die darauf abzielen, seine Sicherheit zu erhöhen. Daher verbessert SHA-256 trotz der Befolgung der Prinzipien der Merkle-Damgård-Transformation in seinem Polsterschritt die Gesamtsicherheit, indem er andere Sicherheitsmechanismen einführt, die ihn nicht nur auf das grundlegende Rahmenwerk der Merkle-Damgård-Transformation beschränken.

SHA-3 (Secure Hash Algorithm 3)

SHA-3 ist der neueste sichere Hash-Standard, der offiziell vom National Institute of Standards and Technology (NIST) im Jahr 2015 als Federal Information Processing Standard (FIPS 202) genehmigt wurde. SHA-3 soll nicht die vorherigen SHA-1 oder SHA-2 ersetzen (da SHA-2 immer noch als sicher betrachtet wird), sondern vielmehr die SHA-Familie ergänzen und eine alternative Option bieten, die einen anderen kryptografischen Hash-Algorithmus bereitstellt. SHA-3 basiert auf dem Keccak-Algorithmus, der von Guido Bertoni und anderen entwickelt wurde und war der Gewinner des SHA-3-Wettbewerbs, den das NIST im Jahr 2012 abhielt.

Das Arbeitsprinzip von SHA-3 unterscheidet sich erheblich von SHA-2, hauptsächlich weil es eine Methode namens "Schwammkonstruktion" verwendet, um Daten zu absorbieren und auszudrücken und den endgültigen Hash-Wert zu erzeugen. Diese Methode ermöglicht es SHA-3, flexibel Hash-Werte verschiedener Längen auszugeben und damit eine breitere Palette von Anwendungen als SHA-2 anzubieten. Die Hauptschritte von SHA-3 sind wie folgt:

Absorbierende Phase:

In der Absorptionsphase teilt die Schwammstruktur zunächst die Eingabedaten in Blöcke fester Größe auf. Diese Datenblöcke werden nacheinander in den internen Zustand des Schwamms "aufgenommen", der in der Regel größer als ein einzelner Datenblock ist, um sicherzustellen, dass eine große Menge an Daten verarbeitet werden kann, ohne überzulaufen. Spezifisch wird jeder Datenblock in irgendeiner Weise mit einem Teil des internen Zustands verschmolzen (zum Beispiel durch eine XOR-Operation), gefolgt von der Anwendung einer festen Permutationsfunktion (in SHA-3 ist dies Keccak-f), um den gesamten Zustand zu transformieren und somit Störungen zwischen verschiedenen Eingabedatenblöcken zu verhindern. Dieser Vorgang wird wiederholt, bis alle Eingabedatenblöcke verarbeitet wurden.

Keccak-f ist die Kernpermutationsfunktion, die im kryptografischen Hash-Algorithmus SHA-3 verwendet wird. Es ist eine zentrale Komponente der Keccak-Algorithmusfamilie. SHA-3 basiert auf dem Keccak-Algorithmus, der den kryptografischen Hash-Algorithmuswettbewerb des NIST gewonnen und wurde als Standard für SHA-3 ausgewählt. Die Keccak-f-Funktion hat mehrere Varianten, wobei die am häufigsten verwendete Keccak-f[1600] ist, wobei die Zahl die Bitbreite angibt, auf der sie arbeitet.

Keccak-f besteht aus mehreren Runden derselben Operation (Runden genannt). Für Keccak-f[1600] gibt es insgesamt 24 Runden von Operationen. Jede Runde umfasst fünf grundlegende Schritte: θ (Theta), ρ (Rho), π (Pi), χ (Chi) und ι (Iota). Diese Schritte wirken zusammen auf das Zustandsarray und transformieren allmählich seinen Inhalt, um Verwirrung und Diffusion zu erhöhen und die Sicherheit zu verbessern. Im Folgenden finden Sie eine kurze Beschreibung dieser Schritte:

• θ (Theta) Schritt: Führt XOR-Operationen auf allen Bits jeder Spalte durch und führt dann das Ergebnis auf benachbarte Spalten aus, wodurch eine Diffusion zwischen den Spalten entsteht.
• ρ (Rho) Schritt: Bitweise Rotationsoperation, bei der jedes Bit gemäß vorbestimmter Regeln um eine andere Anzahl von Bits rotiert wird, wodurch die Komplexität der Daten erhöht wird.
• π (Pi) Schritt: Ordnet die Bits im Zustandsarray neu an und ändert die Position der Bits, um eine Diffusion über Zeilen und Spalten zu erreichen.
• χ (Chi) Schritt: Ein nichtlinearer Schritt, der XOR-Operationen auf jedem Bit jeder Zeile durchführt, einschließlich sich selbst, seines unmittelbaren Nachbarn und des Komplements des Nachbarn. Dies ist eine lokale Operation, die die nichtlinearen Merkmale des kryptografischen Algorithmus erhöht.
• ι (Iota) Schritt: Führt dem Zustandsarray einen Rundenkonstanten hinzu, wobei die Konstante in jeder Runde unterschiedlich ist, um zu vermeiden, dass alle Runden identisch funktionieren, was Unvorhersehbarkeit einführt.

Keccak-f bietet ein hohes Maß an Sicherheit durch diese Schritte. Sein Design stellt sicher, dass selbst geringfügige Änderungen an der Eingabe zu weit verbreiteten und unvorhersehbaren Änderungen im Zustandsarray führen, die durch die Prinzipien der Verwirrung (erschweren es Angreifern, die Eingabe aus der Ausgabe abzuleiten) und Diffusion (wo geringfügige Änderungen an der Eingabe mehrere Teile der Ausgabe beeinflussen) erreicht werden.

Das Design von Keccak-f ermöglicht die Anpassung von Parametern (wie Zustandsgröße und Anzahl der Runden) über verschiedene Sicherheitsstufen und Anwendungsszenarien hinweg und bietet damit eine hohe Flexibilität. Keccak-f[1600] ist bekannt für seine effiziente Implementierung und erreicht hohe Verarbeitungsgeschwindigkeiten sowohl in Hardware als auch in Software, insbesondere bei der Verarbeitung großer Datenmengen.

Quetschphase:

Sobald alle Eingabedatenblöcke in den internen Zustand aufgenommen wurden, tritt die Schwammstruktur in die Ausquetschphase ein. In diesem Stadium werden Teile des internen Zustands progressiv als Ergebnis der Hash-Funktion ausgegeben. Wenn die benötigte Ausgabelänge die Menge überschreitet, die auf einmal ausgedrückt werden kann, wendet die Schwammstruktur die Permutationsfunktion an, um den internen Zustand erneut zu transformieren, und fährt dann fort, weitere Daten auszugeben. Dieser Prozess wird fortgesetzt, bis die gewünschte Ausgabelänge erreicht ist.

Das Ziel von SHA-3's Design ist es, eine höhere Sicherheit als SHA-2 und eine bessere Widerstandsfähigkeit gegen Quantencomputing-Angriffe zu bieten. Dank seiner einzigartigen Schwammstruktur ist SHA-3 theoretisch in der Lage, alle derzeit bekannten kryptografischen Angriffsmethoden zu widerstehen, einschließlich Kollisionsangriffen, Preimage-Angriffen und Zweit-Preimage-Angriffen.

RIPEMD-160 (RACE Integrity Primitives Evaluation Message Digest)

RIPEMD-160 ist eine kryptografische Hash-Funktion, die entwickelt wurde, um einen sicheren Hash-Algorithmus bereitzustellen. Es wurde 1996 von Hans Dobbertin und anderen entwickelt und ist Mitglied der RIPEMD (RACE Integrity Primitives Evaluation Message Digest)-Familie.

RIPEMD-160 erzeugt einen 160-Bit (20-Byte) Hash-Wert, der der Ursprung der "160" in seinem Namen ist. Es basiert auf dem Design von MD4 und ist von anderen Hash-Algorithmen wie MD5 und SHA-1 beeinflusst. RIPEMD-160 umfasst zwei parallele, ähnliche Operationen, die die Eingabedaten separat verarbeiten und dann die Ergebnisse dieser beiden Prozesse kombinieren, um den endgültigen Hash-Wert zu generieren. Dieses Design zielt darauf ab, die Sicherheit zu erhöhen.

Der Berechnungsprozess von RIPEMD-160 umfasst mehrere grundlegende Schritte: Padding, Blockverarbeitung und Kompression:

• Padding: Die Eingabemitteilung wird zuerst gepaddet, um sicherzustellen, dass ihre Länge modulo 512 Bits 448 Bits entspricht. Das Padding beginnt immer mit einem einzigen Bit von 1, gefolgt von einer Reihe von 0-Bits und endet mit einer 64-Bit-Repräsentation der ursprünglichen Nachrichtenlänge.
• Blockverarbeitung: Die gepaddete Nachricht wird in 512-Bit-Blöcke aufgeteilt.
• Initialisierung: Es verwendet fünf 32-Bit-Register (A, B, C, D, E), die auf bestimmte spezifische Werte initialisiert sind.
• Kompressionsfunktion: Jeder Block wird nacheinander verarbeitet, wobei die Werte dieser fünf Register durch eine Reihe komplexer Operationen aktualisiert werden. Dieser Prozess umfasst bitweise Operationen (wie Addition, UND, ODER, NICHT, zirkuläre Linksverschiebungen) und die Verwendung eines Satzes fester Konstanten.
• Ausgabe: Nachdem alle Blöcke verarbeitet wurden, werden die Werte dieser fünf Register verkettet, um den endgültigen 160-Bit-Hash-Wert zu bilden.