¿Qué es un Valor Hash?

Un valor hash es una cadena o número de tamaño fijo generado a partir de cualquier tamaño de datos de entrada mediante una función hash. Estas funciones aceptan entradas diversas como texto, imágenes y videos, produciendo un valor hash fijo e irreversible. Los valores hash son deterministas, lo que significa que entradas idénticas siempre resultan en la misma salida. También presentan resistencia a colisiones, lo que dificulta encontrar entradas distintas que produzcan la misma salida.

Funciones del Valor Hash

Los valores hash desempeñan roles esenciales en informática y TI, ofreciendo un resumen de longitud fija de los datos independientemente de su tamaño. Estas funciones facilitan diversas aplicaciones:

• Verificación de Integridad de Datos: Se utiliza para verificar si los datos permanecen sin modificaciones durante la transmisión, asegurando la integridad de los archivos descargados.
• Almacenamiento de Contraseñas: Las contraseñas se almacenan como valores hash por seguridad, lo que dificulta recuperar las contraseñas originales de bases de datos comprometidas.
• Recuperación Rápida de Datos: Los valores hash actúan como índices en tablas hash, permitiendo operaciones de datos eficientes.
• Deduplicación de Datos: Ayuda a identificar y eliminar elementos de datos duplicados comparando valores hash.
• Firma Digital y Verificación: Asegura la integridad de los datos y el origen mediante criptografía de clave pública y funciones hash.
• Tecnología Blockchain: Utiliza valores hash para asegurar los registros de transacciones y garantizar la inmutabilidad de los datos.
• Marcas de Tiempo a Prueba de Manipulaciones: Proporciona una marca de tiempo irreversible para los datos, útil en protecciones legales y de derechos de autor.

La razón por la que los valores hash son efectivos en estas áreas se debe a sus características clave de rapidez, determinismo, irreversibilidad y resistencia a colisiones. Utilizadas correctamente, las funciones hash pueden proporcionar un soporte robusto en la seguridad de los datos, mejorar la eficiencia y verificar la autenticidad de la información.

¿Qué es una Función Hash?

Una función hash es una construcción matemática que mapea datos de entrada (o "mensaje") a una cadena de tamaño fijo, típicamente un valor numérico, como se ilustra en el diagrama a continuación. Ampliamente utilizada en la gestión de datos y la seguridad de la información, una función hash se caracteriza por su eficiente rendimiento computacional, longitud de salida consistente, irreversibilidad, sensibilidad a las variaciones de entrada y resistencia a colisiones.

Rendimiento Computacional Eficiente

Las funciones hash pueden calcular rápidamente valores hash a partir de datos de cualquier forma, independientemente del tamaño de los datos. Esta característica es crucial para aplicaciones que requieren acceso rápido a datos, como las tablas hash. Esto se debe a que, al almacenar datos en tablas hash, la velocidad de la función hash determina la velocidad de recuperación de datos. Las tablas hash utilizan funciones hash para localizar rápidamente el lugar de almacenamiento de los datos, confiando en la rápida capacidad computacional de las funciones hash.

Además, en sistemas que necesitan procesar grandes cantidades de datos, la eficiencia de las funciones hash impacta directamente en el rendimiento general del sistema. Si una función hash funciona lentamente, se convertirá en un cuello de botella en el rendimiento del sistema. Algunos sistemas en tiempo real, como el filtrado de paquetes en dispositivos de red, requieren el cálculo inmediato de valores hash para los datos para tomar decisiones rápidas. En estos casos, la eficiencia de las funciones hash es igualmente crucial.

Por ejemplo, considere una plataforma de comercio electrónico en línea donde los usuarios pueden ingresar nombres de productos en la barra de búsqueda para encontrar productos. El sistema backend puede usar funciones hash para localizar rápidamente la información del producto almacenada en tablas hash. Si el proceso de cálculo de la función hash es lento, la experiencia del usuario se verá gravemente afectada, ya que tendrán que esperar más tiempo para obtener resultados de búsqueda. En esta situación, el rendimiento computacional eficiente de las funciones hash garantiza tiempos de respuesta rápidos, mejorando así la experiencia del usuario. [Aprender Más]

Consistencia en la Longitud de Salida en Funciones Hash

Las funciones hash convierten la entrada de cualquier longitud en una salida de longitud fija a través de una serie compleja de cálculos. Este proceso a menudo implica dividir los datos de entrada en bloques de tamaño fijo (para aquellas entradas que exceden el tamaño de la unidad de procesamiento), aplicando una serie de operaciones matemáticas y lógicas a cada bloque, y luego combinando o acumulando los resultados de estas operaciones de alguna manera para producir finalmente un valor hash de tamaño fijo.

¿Por qué es importante? La consistencia de la longitud de salida ayuda a garantizar la seguridad de las funciones hash. Si la longitud de la salida del hash pudiera variar, podría filtrar información sobre el tamaño de los datos originales, lo cual podría ser explotado potencialmente para atacar el sistema en algunos escenarios. Además, una longitud de salida fija también dificulta que los atacantes infieran características de los datos de entrada al analizar la longitud de la salida. Al mismo tiempo, las salidas de longitud fija simplifican el almacenamiento y la comparación de valores hash. Los diseñadores de sistemas pueden saber de antemano cuánto espacio ocupará cada valor hash, lo cual es muy importante para escenarios como el diseño de bases de datos y la transmisión de red. Además, la consistencia de la longitud de salida se vuelve muy eficiente para comparar si los valores hash son iguales porque solo requiere comparar datos de una longitud fija. Esto es particularmente importante cuando se utilizan tablas hash para la rápida recuperación de datos.

Tomando SHA-256 como ejemplo, esta función hash criptográfica ampliamente utilizada siempre produce un valor hash de 256 bits (es decir, 32 bytes), independientemente de si los datos de entrada son un solo byte o varios millones de bytes. Esta consistencia asegura que los valores hash SHA-256 se puedan utilizar para diversas aplicaciones de seguridad, como firmas digitales y Códigos de Autenticación de Mensajes (MAC), mientras simplifica el flujo de trabajo de procesamiento y almacenamiento de datos.

Irreversibilidad de las Funciones Hash

Las funciones hash son unidireccionales, lo que significa que es imposible inferir los datos originales a partir del valor hash. Esta característica es particularmente importante al almacenar contraseñas, ya que incluso si la base de datos se ve comprometida, los atacantes no pueden recuperar las contraseñas a partir de los valores hash. La irreversibilidad de las funciones hash se basa principalmente en los siguientes principios y características:

• Compresión: Las funciones hash pueden mapear entradas de cualquier longitud (que pueden ser muy grandes en uso práctico) a una salida de longitud fija. Esto significa que hay infinitamente muchas entradas posibles mapeadas a un número finito de salidas. Dado que el espacio de salida (valores hash) es mucho menor que el espacio de entrada, diferentes entradas producirán inevitablemente la misma salida, un fenómeno conocido como "colisión". Debido a esta compresión, es imposible determinar la entrada específica a partir de una salida dada (valor hash).
• Alta no linealidad y complejidad: Las funciones hash están diseñadas utilizando operaciones matemáticas y lógicas complejas (como operaciones a nivel de bits, operaciones de módulo, etc.) para asegurar que la salida sea altamente sensible a la entrada. Incluso cambios menores en la entrada (por ejemplo, cambiar un bit) pueden provocar cambios significativos e impredecibles en la salida (valor hash). Este alto grado de no linealidad y la aleatoriedad de la salida hacen extremadamente difícil deducir la entrada original a partir del valor hash.
• Unidireccionalidad: El diseño de las funciones hash asegura que su operación sea unidireccional; es decir, mientras que calcular el valor hash es fácil, el proceso inverso (recuperar los datos originales a partir del valor hash) no es factible. Esto se debe a que el proceso de cálculo de las funciones hash implica una serie de operaciones irreversibles (como la irreversibilidad de las operaciones de módulo), asegurando que incluso con el valor hash, es imposible reconstruir los datos originales.
• Mapeo aleatorio: Una función hash ideal debería actuar como un "mapeador aleatorio", lo que significa que cada entrada posible tiene la misma probabilidad de ser mapeada a cualquier punto en el espacio de salida. Esta propiedad asegura que no hay una manera factible de predecir a qué salida se mapeará una entrada específica, mejorando la irreversibilidad de la función hash.
• Base matemática: Matemáticamente, la irreversibilidad de las funciones hash se puede entender a través de su dependencia en "problemas de logaritmo discreto", "problemas de factorización de enteros grandes" u otros problemas de teoría de números que son difíciles de resolver con las capacidades matemáticas y computacionales actuales. Por ejemplo, el diseño de algunos algoritmos hash puede depender indirectamente de la dificultad computacional de estos problemas, asegurando así su irreversibilidad.

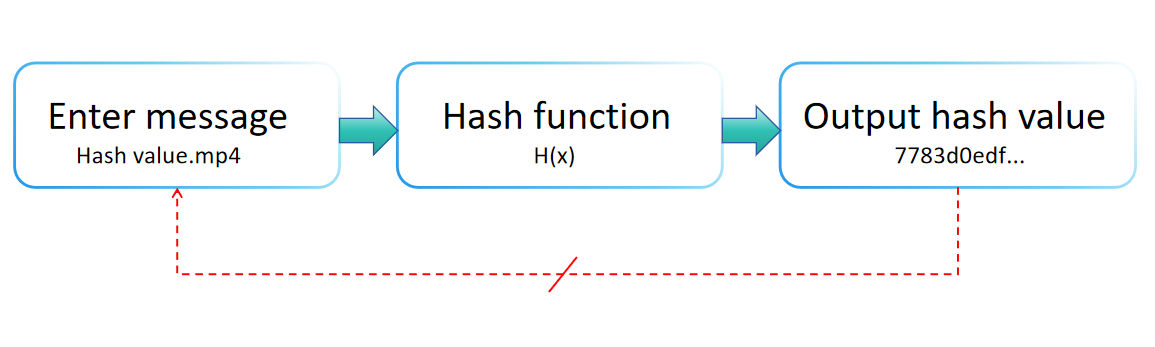
Sensibilidad de Entrada y el Efecto Avalancha

En el diseño de las funciones hash, se utilizan operaciones matemáticas y lógicas complejas (como operaciones a nivel de bits, operaciones módulo, etc.) para asegurar que la salida sea altamente sensible a la entrada. Incluso cambios menores en la entrada (por ejemplo, cambiar un solo bit) resultarán en cambios significativos e impredecibles en la salida (el valor hash), un fenómeno conocido como el "efecto avalancha". [Aprender Más]

Resistencia a Colisiones en Criptografía

La resistencia a colisiones de una función hash es un concepto crucial en criptografía, indicando el nivel de seguridad de una función hash contra ataques de colisión. Esta propiedad implica que para cualquier función hash H, encontrar dos entradas distintas x y y (x ≠ y) tales que H(x) = H(y) es computacionalmente inviable. Una función hash con una resistencia a colisiones robusta hace que sea extremadamente desafiante encontrar dos entradas diferentes que conduzcan al mismo valor de salida.

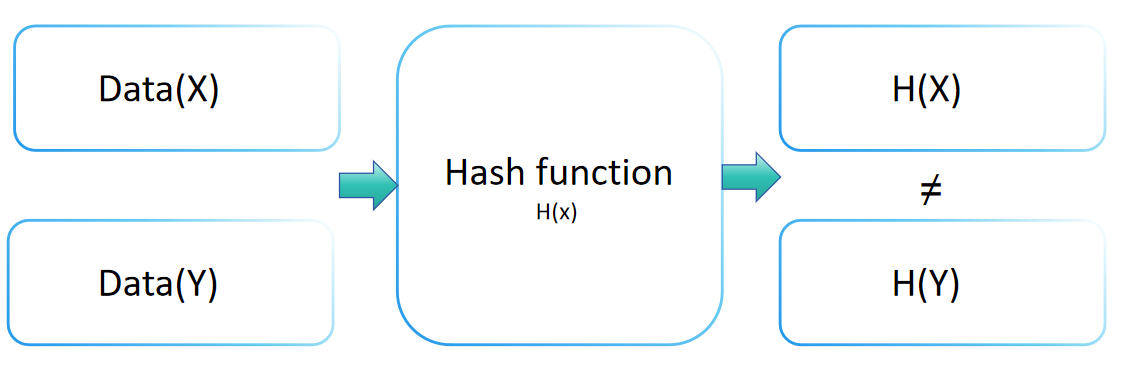
La resistencia a colisiones juega un papel vital en el mantenimiento de la integridad de los datos y la verificación. Al transformar la información de entrada en una salida de tamaño fijo (o resumen), las funciones hash aseguran que no dos entradas diferentes produzcan la misma salida. Esta característica única permite que el valor hash identifique con precisión el valor original.

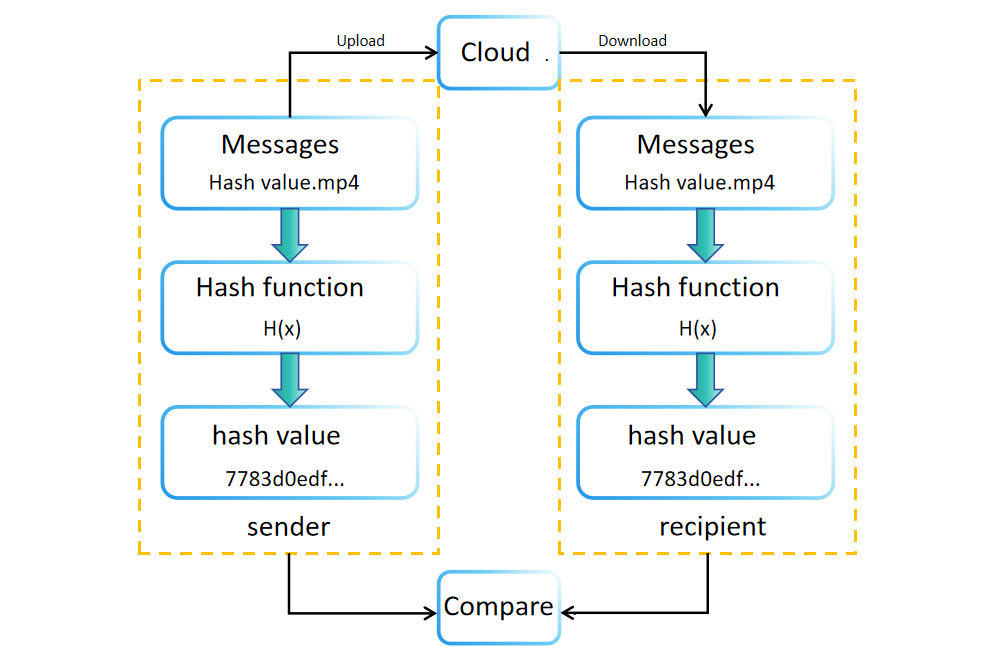
Durante la creación o almacenamiento de datos, se genera un valor hash (o resumen) utilizando una función hash. Este valor se almacena o transmite junto con los datos originales. Por ejemplo, los sitios de descarga de software a menudo muestran valores hash de archivos para la verificación de integridad. Los destinatarios pueden recalcular de forma independiente el valor hash de los datos recibidos para confirmar su integridad. Si los valores hash originales y recalculados coinciden, se verifica la integridad de los datos. Si no, los datos pueden haber sido manipulados o corrompidos durante la transmisión o almacenamiento.

Comparar los valores hash también ofrece la ventaja de verificar la integridad de los datos sin requerir un espacio de almacenamiento significativo. Este método permite a los destinatarios confirmar la autenticidad de los datos simplemente comparando los valores hash antes y después de la transmisión.

¿Se pueden encontrar colisiones de hash?

A través de las características de las funciones hash mencionadas anteriormente, hemos comprendido la resistencia a colisiones. Pero, ¿es posible que existan colisiones de hash, es decir, que dos entradas diferentes produzcan la misma salida? La respuesta es afirmativa, las colisiones existen de hecho. Según el principio del palomar, siempre que el espacio de entrada sea lo suficientemente grande, existe la posibilidad de colisiones de hash. Esto se debe a que el espacio de salida de las funciones hash suele ser mucho más pequeño que el espacio de entrada, lo que inevitablemente lleva a que múltiples entradas diferentes se asignen a la misma salida.

El principio del palomar es un principio simple e intuitivo de la matemática combinatoria, que establece que si se colocan más de n objetos en n contenedores, entonces al menos un contenedor contendrá dos o más objetos. Este principio también se puede usar para explicar problemas como la paradoja del cumpleaños.

La aplicación del principio del palomar es muy amplia, con usos importantes en campos como la criptografía, la informática y las matemáticas. Por ejemplo, en informática, el principio del palomar se utiliza para demostrar la corrección de ciertos algoritmos o para analizar la complejidad temporal de los algoritmos. En criptografía, el principio del palomar también se utiliza para diseñar ciertos métodos de ataque criptográfico, como el ataque de cumpleaños.

La paradoja del cumpleaños es una aplicación clásica del principio del palomar. Supongamos que hay n personas en una sala. Si queremos que la probabilidad de que al menos dos personas compartan el mismo cumpleaños sea mayor al 50%, ¿cuántas personas se necesitan? Según el principio del palomar, si 367 personas (asumiendo que hay 366 días en un año, más un día adicional para el 29 de febrero en un año bisiesto) se colocan en 366 "palomares" (es decir, cumpleaños), entonces al menos un "palomar" contendrá a dos personas, lo que significa que al menos dos personas comparten el mismo cumpleaños. Esto ilustra la paradoja del cumpleaños.

Es importante señalar que, aunque el principio del palomar es simple e intuitivo, su aplicación debe considerar el contexto específico. Por ejemplo, al aplicar el principio del palomar, es necesario asegurar que las variables aleatorias involucradas sean independientes entre sí; de lo contrario, puede llevar a conclusiones incorrectas. Además, en algunos casos, también es necesario considerar factores como el tamaño y la forma de los palomares.

Sin embargo, intentar encontrar colisiones de hash simplemente recorriendo el espacio de entrada puede no ser práctico, principalmente por dos razones:

• Complejidad computacional: Para la mayoría de las funciones hash, el espacio de entrada es vasto. Tomando SHA-256 como ejemplo; su salida es un valor hash de 256 bits, lo que significa que tiene 2^256 posibles salidas. Dado que uno de los objetivos de diseño de las funciones hash es minimizar las colisiones tanto como sea posible, teóricamente, encontrar una colisión de hash para SHA-256 requeriría recorrer aproximadamente 2^(256/2) = 2^128 entradas, según la paradoja del cumpleaños, que es el número aproximado de entradas esperadas para encontrar una colisión. Incluso con los supercomputadores más potentes actualmente disponibles, llevaría mucho más allá de una vida humana completar tal tarea, considerándose imposible encontrar una colisión de hash SHA-256 mediante un simple recorrido.
• Diseño de funciones hash: Las funciones hash están diseñadas típicamente para que encontrar colisiones sea computacionalmente inviable. Esto significa que, aunque teóricamente existen colisiones, en la práctica es prácticamente imposible encontrarlas. Esta es una característica importante de las funciones hash criptográficas (como SHA-256), que se utilizan ampliamente en áreas como firmas digitales, almacenamiento de contraseñas y más.

Por supuesto, también podemos usar algoritmos específicos para intentar encontrar colisiones de hash. Estos algoritmos a menudo explotan algunas propiedades o debilidades conocidas de las funciones de hash para encontrar colisiones. Aquí hay algunas técnicas y métodos comunes para encontrar colisiones de hash:

• Ataque de Cumpleaños: Este es un método simple basado en la probabilidad utilizado para estimar el tiempo requerido para encontrar una colisión cuando las entradas se eligen al azar. El principio del ataque de cumpleaños es que si hay muchas personas en una habitación, la probabilidad de que dos personas tengan el mismo cumpleaños aumenta con el número de personas. De manera similar, en las funciones de hash, si se selecciona un número suficiente de entradas de manera aleatoria, es probable que dos entradas eventualmente produzcan el mismo resultado de hash.
• Ataque de Fuerza Bruta: Este es el método más directo, que implica recorrer todas las posibles entradas para encontrar una colisión. Sin embargo, este método es impracticable para funciones de hash con grandes espacios de entrada debido a los enormes recursos computacionales y tiempo requerido.
• Tablas Arcoíris: Esta técnica se utiliza para precalcular y almacenar un gran número de valores hash y sus entradas correspondientes. Las tablas arcoíris son especialmente útiles para descifrar contraseñas que no han utilizado ofuscación de datos aleatorios o tienen una función de hash conocida. Al buscar en la tabla arcoíris, un atacante puede encontrar rápidamente una entrada que coincida con un valor de hash específico.
• Ataques de Extensión de Hash: Ciertas funciones de hash permiten a los atacantes combinar datos adicionales con un valor de hash conocido sin conocer la entrada original, generando así un nuevo valor de hash. Este ataque puede usarse para construir colisiones o realizar otros tipos de ataques.
• Entradas Construidas Especialmente: A veces, los atacantes pueden explotar debilidades específicas o comportamientos no lineales en las funciones de hash para construir entradas especiales que tienen más probabilidades de producir colisiones en la función de hash.

¿Cuáles son las funciones hash más utilizadas?

MD5 (Algoritmo de Resumen de Mensaje 5)

MD5 es una función hash criptográfica ampliamente utilizada, diseñada por Ronald Rivest en la década de 1990 para reemplazar el antiguo algoritmo MD4. Puede convertir un mensaje de cualquier longitud en un valor hash de longitud fija (128 bits o 16 bytes). El objetivo de diseño de MD5 era proporcionar una forma rápida y relativamente segura de generar una huella digital de los datos. Sin embargo, se han descubierto métodos de colisión para MD5, lo que ha hecho que el algoritmo sea inseguro, pero aún se utiliza ampliamente en situaciones donde la seguridad no es una preocupación primordial.

El proceso de cálculo de MD5 implica los siguientes pasos:

• Relleno: Inicialmente, los datos originales se rellenan para que su longitud en bytes sea un múltiplo de 512. El relleno comienza con un 1, seguido de 0s hasta que se cumple el requisito de longitud.
• Agregando Longitud: Un valor de longitud de 64 bits, que es la representación binaria de la longitud del mensaje original, se añade al mensaje rellenado, haciendo que la longitud final del mensaje sea un múltiplo de 512 bits.
• Inicializando el Buffer MD: Cuatro registros de 32 bits (A, B, C, D) se inicializan para almacenar los valores hash intermedios y finales.
• Procesando Bloques de Mensajes: El mensaje rellenado y procesado por longitud se divide en bloques de 512 bits, y cada bloque se procesa a través de cuatro rondas de operación. Cada ronda incluye 16 operaciones similares basadas en funciones no lineales (F, G, H, I), operaciones de desplazamiento circular izquierdo y adición módulo 32.
• Salida: El valor hash final es el contenido del último estado de los cuatro registros A, B, C, D concatenados (cada registro es de 32 bits), formando un valor hash de 128 bits.

SHA-1 (Algoritmo Hash Seguro 1)

SHA-1 fue diseñado por la Agencia de Seguridad Nacional de EE. UU. (NSA) y publicado como un Estándar de Procesamiento de Información Federal (FIPS PUB 180-1) por el Instituto Nacional de Estándares y Tecnología (NIST) en 1995. SHA-1 está destinado para su uso en firmas digitales y otras aplicaciones criptográficas, generando un valor hash de 160 bits (20 bytes) conocido como un resumen de mensaje. Aunque ahora se sabe que SHA-1 tiene vulnerabilidades de seguridad y ha sido reemplazado por algoritmos más seguros como SHA-256 y SHA-3, entender su principio de funcionamiento aún tiene valor educativo e histórico.

El propósito de diseño de SHA-1 es tomar un mensaje de longitud arbitraria y producir un resumen de mensaje de 160 bits para verificar la integridad de los datos. Su proceso de cálculo se puede dividir en los siguientes pasos:

• Relleno: Inicialmente, el mensaje original se rellena para que su longitud (en bits) módulo 512 sea igual a 448. El relleno siempre comienza con un bit "1", seguido de varios bits "0", hasta que se cumple la condición de longitud anterior.
• Agregando Longitud: Un bloque de 64 bits se añade al mensaje rellenado, representando la longitud del mensaje original (en bits), haciendo que la longitud final del mensaje sea un múltiplo de 512 bits.
• Inicializando el Buffer: El algoritmo SHA-1 utiliza un buffer de 160 bits, dividido en cinco registros de 32 bits (A, B, C, D, E), para almacenar los valores hash intermedios y finales. Estos registros se inicializan con valores constantes específicos al comienzo del algoritmo.
• Procesando Bloques de Mensajes: El mensaje preprocesado se divide en bloques de 512 bits. Para cada bloque, el algoritmo ejecuta un bucle principal que contiene 80 pasos similares. Estos 80 pasos se dividen en cuatro rondas, cada una con 20 pasos. Cada paso utiliza una función no lineal diferente (F, G, H, I) y una constante (K). Estas funciones están diseñadas para aumentar la complejidad y la seguridad de las operaciones. En estos pasos, el algoritmo utiliza operaciones a nivel de bits (como AND, OR, XOR, NOT) y adición módulo 32, así como desplazamientos circulares izquierdos.
• Salida: Después de procesar todos los bloques, los valores acumulados en los cinco registros se concatenan para formar el valor hash final de 160 bits.

SHA-2 (Algoritmo Hash Seguro 2)

SHA-2 es una familia de funciones hash criptográficas, que incluye varias versiones diferentes, consistiendo principalmente en seis variantes: SHA-224, SHA-256, SHA-384, SHA-512, SHA-512/224 y SHA-512/256. SHA-2 fue diseñado por la Agencia de Seguridad Nacional de Estados Unidos (NSA) y publicado como un Estándar de Procesamiento de Información Federal (FIPS) por el Instituto Nacional de Estándares y Tecnología (NIST). En comparación con su predecesor, SHA-1, SHA-2 ofrece una seguridad mejorada, reflejada principalmente en valores hash más largos y una resistencia más fuerte a ataques de colisión.

La operación de la familia SHA-2 es similar a SHA-1 en muchos aspectos pero proporciona mayor seguridad mediante el uso de valores hash más largos y un procedimiento de procesamiento más complejo. Aquí están los pasos principales del algoritmo SHA-2:

• Relleno: El mensaje de entrada se rellena primero para hacer que su longitud, menos 64 bits, sea igual a 448 o 896 en una base módulo 512 (para SHA-224 y SHA-256) o módulo 1024 (para SHA-384 y SHA-512). El método de relleno es el mismo que SHA-1, que implica agregar un "1" al final del mensaje, seguido de varios "0"s, y finalmente una representación binaria de 64 bits (para SHA-224 y SHA-256) o 128 bits (para SHA-384 y SHA-512) de la longitud original del mensaje en bits.
• Inicialización del Buffer: El algoritmo SHA-2 utiliza un conjunto de valores hash inicializados como el buffer de inicio, dependiendo de la variante de SHA-2 elegida. Por ejemplo, SHA-256 utiliza ocho registros de 32 bits, mientras que SHA-512 utiliza ocho registros de 64 bits. Estos registros se inicializan a valores constantes específicos.
• Procesamiento de Bloques de Mensajes: El mensaje rellenado se divide en bloques de 512 bits o 1024 bits, y cada bloque se somete a múltiples rondas de operaciones criptográficas. SHA-256 y SHA-224 realizan 64 rondas de operaciones, mientras que SHA-512, SHA-384, SHA-512/224 y SHA-512/256 realizan 80 rondas. Cada ronda de operación incluye una serie de operaciones complejas a nivel de bits, incluyendo operaciones lógicas, adición modular y operaciones condicionales, basándose en diferentes funciones no lineales y constantes predefinidas. Estas operaciones aumentan la complejidad y seguridad del algoritmo.
• Salida: Finalmente, después de procesar todos los bloques, los valores en el buffer se combinan para formar el valor hash final. Dependiendo de la variante de SHA-2, este valor hash puede ser de 224, 256, 384 o 512 bits de longitud.

Podrías preguntarte por qué la entrada a una función hash puede ser de longitud arbitraria, pero la salida es fija. La razón es que la familia SHA-2 utiliza la transformación de Merkle-Damgård, que permite la construcción de funciones hash que pueden procesar mensajes de cualquier longitud a partir de una función de compresión de longitud fija. La transformación de Merkle-Damgård se adopta en muchas funciones hash tradicionales, incluyendo MD5 y SHA-1.

La idea central de la transformación de Merkle-Damgård es dividir el mensaje de entrada en bloques de tamaño fijo y luego procesar estos bloques uno por uno, donde cada paso de procesamiento depende del resultado del anterior, produciendo finalmente un valor hash de tamaño fijo. El paso de relleno de SHA-256 encarna los principios básicos de la transformación de Merkle-Damgård, es decir, mediante el relleno adecuado para procesar mensajes de cualquier longitud y asegurando que la longitud final del mensaje procesado cumpla ciertas condiciones (como ser un múltiplo de una longitud fija). Por lo tanto, se puede decir que el paso de relleno de SHA-256 sigue el método de transformación de Merkle-Damgård.

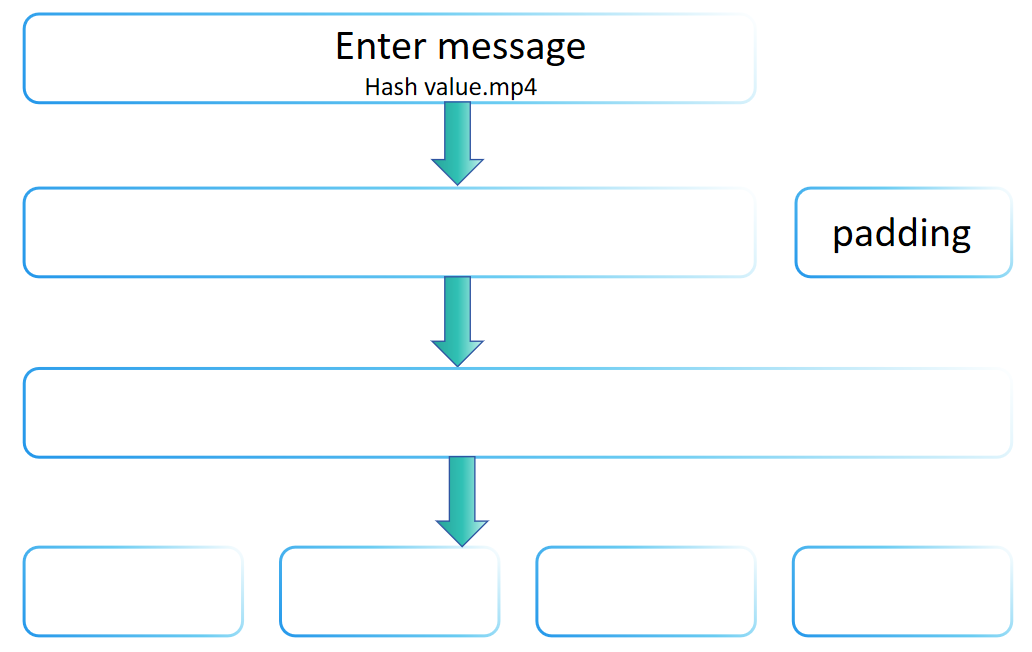
Sin embargo, SHA-256 no es simplemente una implementación directa de la transformación de Merkle-Damgård. También incluye una serie de pasos computacionales complejos (como la expansión del mensaje, múltiples rondas de funciones de compresión, etc.), que son diseños únicos de SHA-256, destinados a mejorar su seguridad. Por lo tanto, aunque SHA-256 sigue los principios de la transformación de Merkle-Damgård en su paso de relleno, mejora la seguridad general introduciendo otros mecanismos de seguridad, haciéndolo no solo limitado al marco básico de la transformación de Merkle-Damgård.

SHA-3 (Algoritmo Hash Seguro 3)

SHA-3 es el último estándar de hash seguro, aprobado oficialmente por el Instituto Nacional de Estándares y Tecnología (NIST) en 2015 como un Estándar de Procesamiento de Información Federal (FIPS 202). SHA-3 no tiene la intención de reemplazar a los anteriores SHA-1 o SHA-2 (ya que SHA-2 todavía se considera seguro), sino más bien complementar y ofrecer una opción alternativa dentro de la familia SHA, proporcionando un algoritmo de hash criptográfico diferente. SHA-3 se basa en el algoritmo Keccak, diseñado por Guido Bertoni y otros, y fue el ganador de la competencia SHA-3 organizada por el NIST en 2012.

El principio de funcionamiento de SHA-3 difiere significativamente de SHA-2, principalmente porque utiliza un método conocido como "construcción de esponja" para absorber y exprimir datos, produciendo el valor hash final. Este método permite que SHA-3 produzca de manera flexible valores hash de diferentes longitudes, ofreciendo así una gama más amplia de aplicaciones que SHA-2. Los pasos principales de SHA-3 son los siguientes:

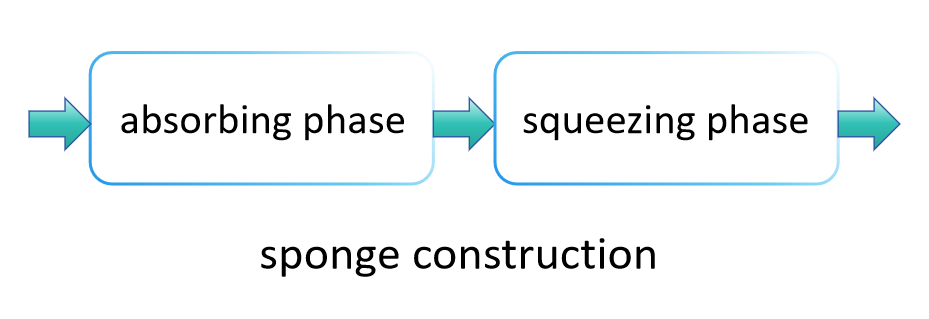
Fase de absorción:

En la fase de absorción, la estructura de esponja primero divide los datos de entrada en bloques de tamaño fijo. Estos bloques de datos se "absorben" secuencialmente en el estado interno de la esponja, que es típicamente más grande que un solo bloque de datos, para asegurar que se pueda procesar una gran cantidad de datos sin desbordamiento. Específicamente, cada bloque de datos se fusiona con una parte del estado interno de alguna manera (como por una operación XOR), seguido por la aplicación de una función de permutación fija (en SHA-3, esta es Keccak-f) para transformar todo el estado, evitando así la interferencia entre diferentes bloques de datos de entrada. Este proceso se repite hasta que todos los bloques de datos de entrada hayan sido procesados.

Keccak-f es la función de permutación central utilizada en el algoritmo hash criptográfico SHA-3. Es un componente central de la familia de algoritmos Keccak. SHA-3 se basa en el algoritmo Keccak, que ganó la competencia de algoritmos hash criptográficos organizada por el NIST y fue seleccionado como el estándar para SHA-3. La función Keccak-f tiene varias variantes, siendo la más comúnmente utilizada Keccak-f[1600], donde el número indica el ancho de bits en el que opera.

Keccak-f está compuesto por múltiples rondas de la misma operación (llamadas rondas). Para Keccak-f[1600], hay un total de 24 rondas de operaciones. Cada ronda incluye cinco pasos básicos: θ (Theta), ρ (Rho), π (Pi), χ (Chi) e ι (Iota). Estos pasos actúan juntos sobre el arreglo de estado, transformando gradualmente su contenido, aumentando la confusión y difusión para mejorar la seguridad. A continuación, se proporciona una breve descripción de estos pasos:

• θ (Theta) paso: Realiza operaciones XOR en todos los bits de cada columna, luego XOR el resultado en columnas adyacentes, proporcionando difusión entre columnas.
• ρ (Rho) paso: Operación de rotación a nivel de bit, donde cada bit se rota un número diferente de bits según reglas predeterminadas, aumentando la complejidad de los datos.
• π (Pi) paso: Reorganiza los bits en el arreglo de estado, cambiando la posición de los bits para lograr difusión a través de filas y columnas.
• χ (Chi) paso: Un paso no lineal que realiza operaciones XOR en cada bit de cada fila, incluyendo a sí mismo, su vecino inmediato y el complemento del vecino. Esta es una operación local que aumenta las características no lineales del algoritmo criptográfico.
• ι (Iota) paso: Introduce una constante de ronda en parte del arreglo de estado, con la constante difiriendo en cada ronda, para evitar que todas las rondas operen idénticamente, introduciendo imprevisibilidad.

Keccak-f proporciona un alto nivel de seguridad a través de estos pasos. Su diseño asegura que incluso cambios menores en la entrada lleven a cambios generalizados e impredecibles en el arreglo de estado, logrados a través de los principios de confusión (haciendo difícil para los atacantes inferir la entrada a partir de la salida) y difusión (donde cambios menores en la entrada afectan múltiples partes de la salida).

El diseño de Keccak-f permite la ajustabilidad de parámetros (como el tamaño del estado y el número de rondas) a través de diferentes niveles de seguridad y escenarios de aplicación, ofreciendo gran flexibilidad. Keccak-f[1600] es conocido por su implementación eficiente, logrando altas velocidades de procesamiento tanto en hardware como en software, especialmente al manejar grandes cantidades de datos.

Fase de extracción:

Una vez que todos los bloques de datos de entrada han sido absorbidos en el estado interno, la estructura de esponja entra en la fase de extracción. En esta etapa, partes del estado interno se van extrayendo progresivamente como resultado de la función hash. Si la longitud de salida requerida excede la cantidad que se puede exprimir de una vez, la estructura de esponja aplica la función de permutación para transformar nuevamente el estado interno, y luego continúa extrayendo más datos. Este proceso se lleva a cabo hasta que se alcanza la longitud de salida deseada.

El objetivo del diseño de SHA-3 es proporcionar mayor seguridad que SHA-2 y mejor resistencia contra ataques informáticos cuánticos. Gracias a su estructura única de esponja, SHA-3 es teóricamente capaz de resistir todos los métodos de ataque criptográfico conocidos actualmente, incluyendo ataques de colisión, ataques de preimagen y ataques de segunda preimagen.

RIPEMD-160 (Digesto de Mensaje de Evaluación de Primitivas de Integridad RACE)

RIPEMD-160 es una función hash criptográfica diseñada para proporcionar un algoritmo de hashing seguro. Fue desarrollado en 1996 por Hans Dobbertin y otros, y es miembro de la familia RIPEMD (Digesto de Mensaje de Evaluación de Primitivas de Integridad RACE).

RIPEMD-160 produce un valor hash de 160 bits (20 bytes), que es el origen del "160" en su nombre. Se basa en el diseño de MD4 e influenciado por otros algoritmos de hashing como MD5 y SHA-1. RIPEMD-160 incluye dos operaciones paralelas, similares que procesan los datos de entrada por separado y luego combinan los resultados de estos dos procesos para generar el valor hash final. Este diseño tiene como objetivo mejorar la seguridad.

El proceso de cálculo de RIPEMD-160 incluye varios pasos básicos: relleno, procesamiento de bloques y compresión:

• Relleno: El mensaje de entrada se rellena primero para asegurar que su longitud módulo 512 bits sea igual a 448 bits. El relleno siempre comienza con un único bit de 1 seguido de una serie de 0 bits, terminando con una representación de 64 bits de la longitud del mensaje original.
• Procesamiento de Bloques: El mensaje rellenado se divide en bloques de 512 bits.
• Inicialización: Utiliza cinco registros de 32 bits (A, B, C, D, E), que se inicializan a ciertos valores específicos.
• Función de Compresión: Cada bloque se procesa por turno, actualizando los valores de estos cinco registros a través de una serie de operaciones complejas. Este proceso incluye operaciones a nivel de bits (como adición, AND, OR, NOT, rotaciones circulares a la izquierda) y el uso de un conjunto de constantes fijas.
• Salida: Después de que todos los bloques han sido procesados, los valores de estos cinco registros se concatenan para formar el valor hash final de 160 bits.